离散化,前缀和,差分

一维前缀和和差分之前学过不再记录

二维情况

前缀和

多维前缀和的普通求解方法几乎都是基于容斥原理

例如有这样一个矩阵,可以视为二维数组:

1 2 4 3
5 1 2 4
6 3 5 9

定义一个矩阵\(sum\)使得\(sum_{x,y}=\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\)那么这个矩阵长这样:

1 3 7 10
6 9 15 22
12 18 29 45

第一个问题是递推求sum的过程,\(sum_{i,j}=sum_{i-1,j}+sum_{i,j-1}-sum_{i-1,j-1}+a_{i,j}\)
因为同时加了\(sum_{i-1,j},sum_{i,j-1}\)重复了\(sum_{i-1,j-1}\)减去
第二个问题是如何应用,譬如求\((x_1,y_1)-(x_2,y_2)\)子矩阵的和
答案\(sum_{x_2,y_2}-sum_{x_1-1,y_2}-sum_{x_2,y_1-1}+sum_{x_1-1,y_1-1}\)

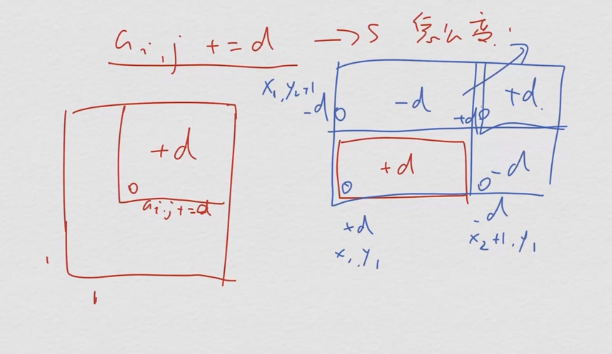
差分

由sum逆推出来,即上述等式改为\(a_{i,j}=sum_{i,j}-sum_{i-1,j}-sum_{i,j-1}+sum_{i-1,j-1}\)

例题

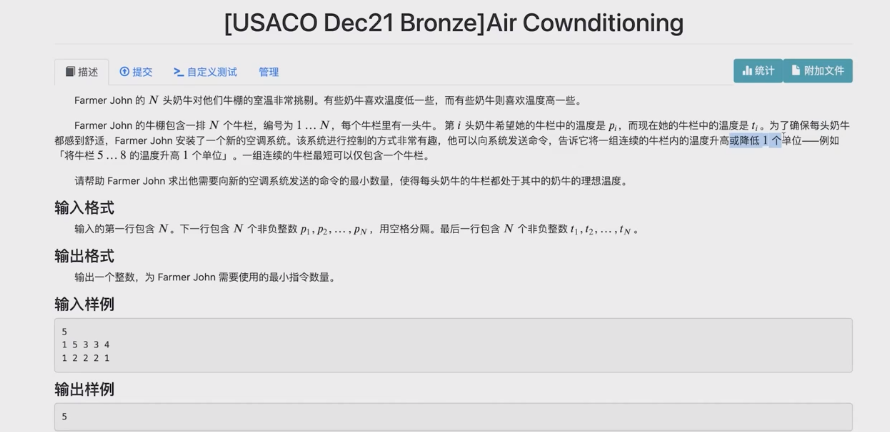
// Problem: Air Cownditioning
// Contest: Virtual Judge - USACO
// URL: https://vjudge.net/problem/USACO-1156
// Memory Limit: 1024 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 1e5+10;
int n,a[N],b[N];
LL ans;
int main()
{	
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&b[i]);
		b[i]-=a[i];
	}
	for(int i=1;i<=n+1;i++)  ans+=max(b[i]-b[i-1],0);
	printf("%lld\n",ans);

	return 0;
}