原题链接:斜率。
题意
在一个平面直角坐标系中,给定 \(n\) 个点的横纵坐标,求出哪两个点所构成的连线的斜率最接近 \(\frac{P}{Q}\)。
数据范围:\(n \le 1000000\)。
思路
显然这是一道数学题,不能直接暴力去找答案。
首先我们可以弱化一下题目,求出斜率最接近 \(y=0\) 即 \(x\) 轴的两点。那我们其实要求的就是斜率的绝对值最小的两点。那么我们可以直接将这 \(n\) 个点按照横坐标的大小排序,然后答案就是组成的线段中斜率的绝对值最小的相邻的两个点。为什么答案一定在相邻两个点中呢?因为如下图所示,对于每一个 \(\bigtriangleup ABC\),都满足性质:\(k_{ac}> \min(k_{ab},k_{bc})\)。
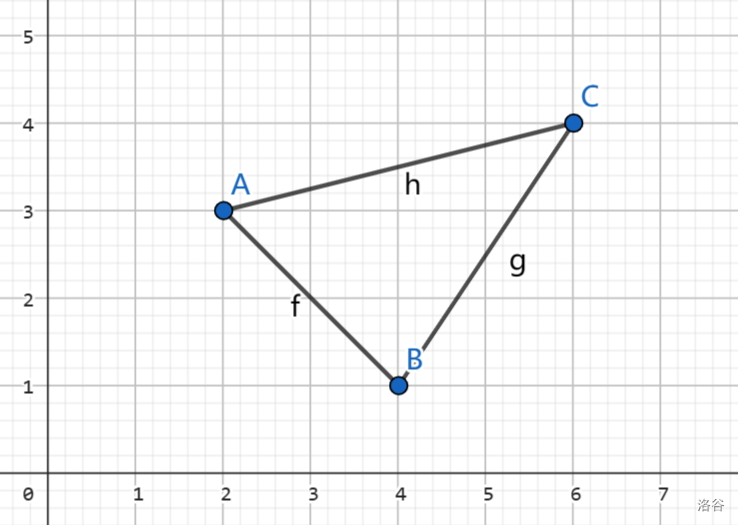
证明:
设三角形三个点的坐标分别为 \(A(a,b),B(e,f),C(c,d)\)。
我们可以用反证法来证明,假设该性质不成立,即 \(k_{ac} \le k_{ab},k_{bc}\),那么:
\(\because\bigtriangleup ABC\),不可能有两边斜率相等。
\(\therefore k_{ac} < k_{ab},k_{bc}\)
\(\because \begin{cases}k_{ac}< k_{ab} \\k_{ac}< k_{bc} \end{cases}\)
\(\therefore \begin{cases}\left|\frac{d-b}{c-a}\right|< \left|\frac{b-f}{a-e}\right| \\\left|\frac{d-b}{c-a}\right|< \left|\frac{d-f}{c-e}\right| \end{cases} \)
\(\because d-b>0,c-a>0,b-f>0,a-e<0,d-f>0,c-e>0\)
化简原不等式得:
\(
\begin{cases}\frac{d-b}{c-a}< \frac{b-f}{e-a}
\\\frac{d-b}{c-a}< \frac{d-f}{c-e}
\end{cases}
\)
不等式两边交叉相乘得:
\(
\begin{cases}de+ab-ad-be<cb+af-ab-cf
\\cd+be-cb-de<cd+af-ad-cf
\end{cases}
\)
\(\therefore \begin{cases}2ab+de+cf<cb+af+ad+be \\be+ad+cf<af+bc+ed \end{cases} \)
两式相减得:\(ed+2ab-be-ad<ad+be-ed\)
\(\therefore 2ab+2ed<2ad+2be\)
\(\therefore ab+ed<ad+be\)
\(\therefore ab-ad<be-ed\)
\(\therefore a\times(b-d)<e\times(b-d)\)
\(\because b-d<0\)
\(\therefore a>e\)
如图所示,显然有 \(a<e\),所以原不等式组无解,于是得证,所以斜率最小的两个点一定是相邻的。
接下来我们来考虑如何求出斜率最接近 \(\frac{P}{Q}\) 的两个点,可以用和上述类似的方法来解答,我们不妨建立一个以现在的直线 \(y=\frac{P}{Q}x\) 为 \(x\) 轴的新的平面直角坐标系,这样问题就转化为了求斜率的绝对值最小的两点,可以用上面所说的做法来实现,但是如何旋转坐标系呢?
我们需要将 \(y=\frac{P}{Q}x\) 这条直线旋转到 \(x\) 轴,设其顺时针旋转了 \(\alpha\) 度,那么这个操作其实等价于将原来坐标系中的每一个点逆时针旋转 \(\alpha\) 度。问题就转化了如何求出一个点逆时针旋转 \(\alpha\) 度后的坐标。
如下图所示设两个点分别是 \(B\) 和 \(D\),\(\angle DAB=\alpha\),\(\angle BAC=\beta\),结论为:若 \(B(x,y)\),则有 \(D(x\cos \alpha - y\sin \alpha,x\sin \alpha + y \cos \alpha)\)。
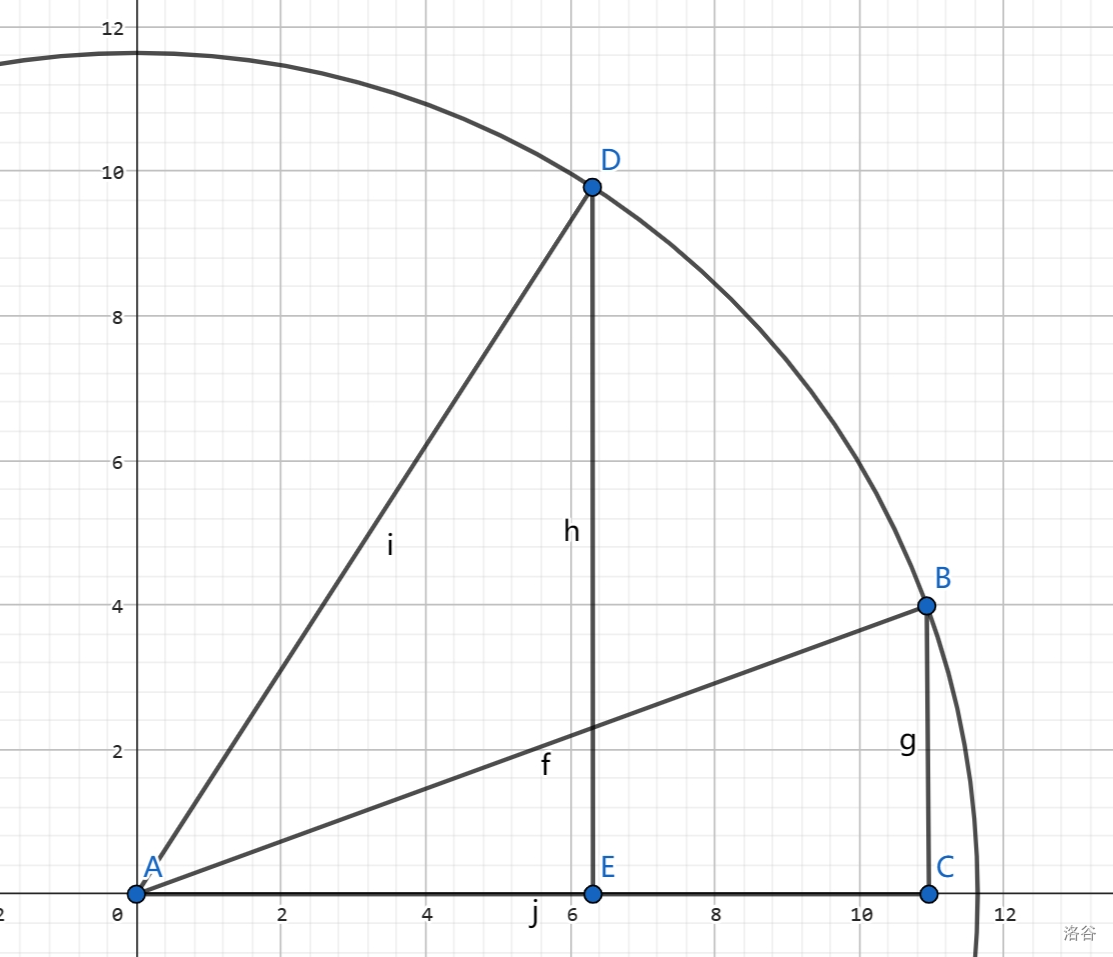
证明:
\(\because B(x,y)\),\(\therefore AC=x,BC=y\)
\(\therefore AB=AD=\frac{x}{\cos \beta}=\frac{y}{\sin \beta}\)
\(\therefore \begin{cases}DE=AD\times \sin\alpha+\beta \\AE=AD\times \cos\alpha+\beta \end{cases} \)
\(\because \begin{cases}\sin\alpha+\beta=\sin \alpha \times \cos \beta+\sin\beta\times \cos \alpha \\\cos\alpha+\beta=\cos\alpha\times\cos\beta-\sin\alpha\times \sin\beta \end{cases} \)(和角公式)
\(\therefore \begin{cases}DE=AD\times (\sin \alpha \times \cos \beta)+AD \times (\sin\beta\times \cos \alpha) \\AE=AD\times (\cos\alpha\times\cos\beta)-AD\times(\sin\alpha\times \sin\beta) \end{cases} \)
将 \(AD=\frac{x}{\cos \beta}=\frac{y}{\sin \beta}\) 带入原不等式得:
\(
\begin{cases}DE=\frac{x}{\cos \beta}\times (\sin \alpha \times \cos \beta)+\frac{y}{\sin \beta} \times (\sin\beta\times \cos \alpha)
\\AE=\frac{x}{\cos \beta}\times (\cos\alpha\times\cos\beta)-\frac{y}{\sin \beta}\times(\sin\alpha\times \sin\beta)
\end{cases}
\)
拆括号得:
\(
\begin{cases}DE=x\times \sin \alpha +y \times \cos \alpha
\\AE=x\times \cos\alpha-y\times \sin\alpha
\end{cases}
\)
又 \(\because D(AE,DE)\)
\(\therefore D(x\cos \alpha - y\sin \alpha,x\sin \alpha + y \cos \alpha)\),得证。
所以最终的做法是:将每个点逆时针旋转后得到新的点,再将新的点按照横坐标排序,答案为相邻两点构成的直线的斜率与 \(y=\frac{P}{Q}\) 的差的最小值。
标签:cos,frac,题解,times,beta,C0328,alpha,1005,sin From: https://www.cnblogs.com/Creeperl/p/17913423.html