Link

ARC169 B Subsegments with Small Sums

Question

\(x\) 是一个序列，定义 \(f(x)\) 为把序列 \(x\) 切成几段，每段的和不能超过 \(S\) 的最小段数

给出序列 \(A=(A_1,A_2,\cdots,A_N)\) 求：

Question

先考虑一个结论，\(x\) 为任意序列，\(f(x)\) 是如何构造的：从头开始，如果这一段的加和超过了 \(S\)，新开一段，否则就把下一个数加到这一段里面，这样分的段数是最少的。

然后思考枚举左端点，观察右端点

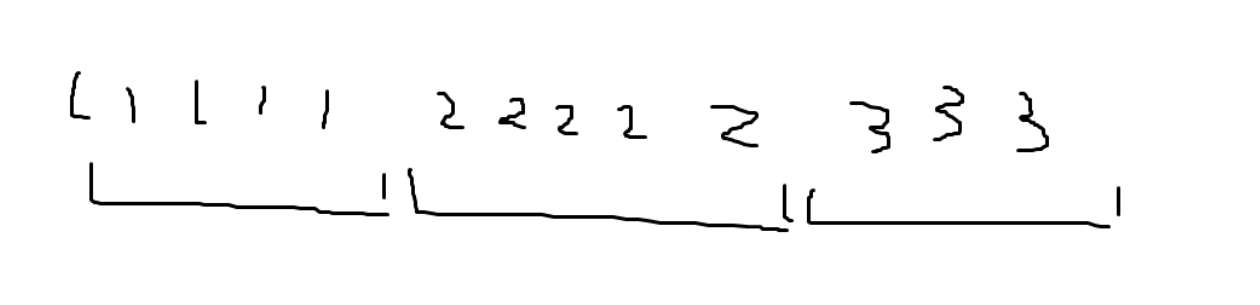
如果右端点在第一个区间里面的画，那么这一段的答案都是 \(1\)，如果右端点在第二个区间里面的画，这一段的答案都是 \(2\)，如果右端点在第三个区间里面的话，这一段的答案都是 \(3\)，以此类推

我们定义 \(F[i]\) 表示以 \(i\) 为左端点，右端点 \(R>i\) 的所有贡献之和，很容易可以得出 \(F[i]=F[nxt[i]+1]+(N-nxt[i])\),其中 \(nxt[i]\) 表示以 \(i\) 为起点的这一段不大于 \(S\) 的终点的位置

反过来刷 DP 或者记忆化 DFS 都能得到答案

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long LL;
const int maxn=25;
int N;LL S,ans,a[maxn];
int nxt[maxn],s[maxn];
int F[maxn];
int DFS(int x) //x开始往后的值
{
    if(F[x]!=-1){
        return F[x];
    }
    if(nxt[x]>N) return F[x]=(N-x+1); 
    return F[x]=(nxt[x]-x)+DFS(nxt[x])+(N-nxt[x]+1);
}
signed main(){
    freopen("B.in","r",stdin);
    scanf("%lld%lld",&N,&S);
    for(int i=1;i<=N;i++) scanf("%lld",&a[i]),s[i]=s[i-1]+a[i];
    for(int i=1;i<=N;i++) F[i]=-1;
    int pos=1;
    for(int i=1;i<=N;i++){
        while(pos<=N&&s[pos]-s[i-1]<=S)
            pos++;
        nxt[i]=pos;
    }
    for(int i=1;i<=N;i++){
        ans+=DFS(i);
    }
    printf("%lld\n",ans);
    return 0;
}