题意：

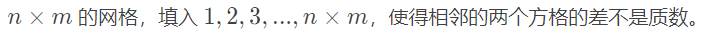
思路：

构造：

$ n $ 行 $ m $ 列，先填奇数行，每行填 $ m $ 个，第 $ 2i - 1 $ 行依次填入 $ (i - 1) \cdot m + 1 $ ， $ (i - 1) \cdot m + 2 $ ， $ ... $ ， $ i \cdot m - 1 $ ， $ i \cdot m $ ，剩下的依次填入偶数行即可。

证明：

构造完成后，对于每行，相邻两项的差值均为 $ 1 $ ，一定不为质数；对于每列，相邻两项的差值均为 $ m $ 的倍数且至少为 $ m $ 的二倍，一定不为质数。