这是一道找规律的题目。
因为我个人习惯,以下部分使用从 \(1\) 开始的下标讲述。
首先我们以 \(1\) 来说:发现在第 \(x\) 行 \(y\) 列的连通块是可以直接连到第 \(1\) 列的,所以很容易可以得出 \(1\) 到 \(y\) 列的连通块数量是 \(2^y-1\)。
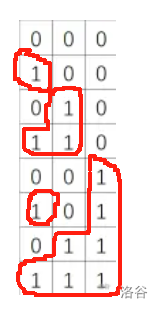
接着,我们考虑再后面的情况:
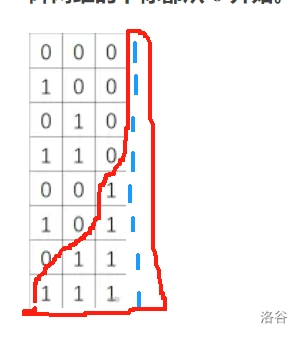
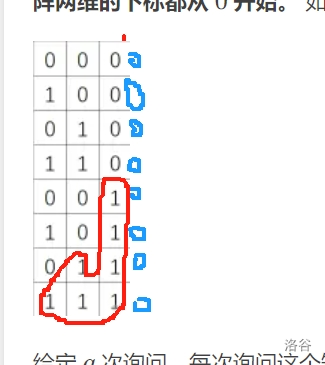
显然,通过观察会分为后面两种情况。一种是遇到了不一样的数字,那么久无法继续判断下去。如果是一样的话那么必定是增加 \(2^{y-1}\) 个连通块,于是,我们就可以用一个循环,一直增加 \(y\),不断更新着连通块的数量。
如果考虑 \(0\) 的情况也是同理。这里不过多解释。
但是我们还是会发现:这样的时间复杂度肯定过不去。
但是出题人给了善良的条件:\(n \le 10^{18}\)。那么 \(\log(n)\) 最多也就 \(64\) 了,所以,我们在 \(y\) 大于 \(64\) 的时候特判掉即可。
于是优化到了 \(O(q \log n)\)。
上代码:link。
其中感谢 @tiger2008 在 求助贴 中告知需要特判。感谢好心人!
给个关注或一个赞呗!
标签:03,连通,题解,特判,64,P9915,RiOI From: https://www.cnblogs.com/gsczl71/p/17891879.html