RLHF · PBRL | B-Pref：生成多样非理性 preference，建立 PBRL benchmark

• 论文题目：B-Pref: Benchmarking Preference-Based Reinforcement Learning，2021 NeurIPS Track Datasets and Benchmarks，7 7 8。
• open review：https://openreview.net/forum?id=ps95-mkHF_
• pdf 版本：https://arxiv.org/pdf/2111.03026.pdf
• html 版本：https://ar5iv.labs.arxiv.org/html/2111.03026

• 0 abstract
• 3 benchmarks environments for PBRL
• 4 algorithmic baselines for PBRL
• 5 使用 B-Pref 分析 PBRL 算法设计
• 6 related work

0 abstract

Reinforcement learning (RL) requires access to a reward function that incentivizes the right behavior, but these are notoriously hard to specify for complex tasks. Preference-based RL provides an alternative: learning policies using a teacher's preferences without pre-defined rewards, thus overcoming concerns associated with reward engineering. However, it is difficult to quantify the progress in preference-based RL due to the lack of a commonly adopted benchmark. In this paper, we introduce B-Pref: a benchmark specially designed for preference-based RL. A key challenge with such a benchmark is providing the ability to evaluate candidate algorithms quickly, which makes relying on real human input for evaluation prohibitive. At the same time, simulating human input as giving perfect preferences for the ground truth reward function is unrealistic. B-Pref alleviates this by simulating teachers with a wide array of irrationalities, and proposes metrics not solely for performance but also for robustness to these potential irrationalities. We showcase the utility of B-Pref by using it to analyze algorithmic design choices, such as selecting informative queries, for state-of-the-art preference-based RL algorithms. We hope that B-Pref can serve as a common starting point to study preference-based RL more systematically. Source code is available at https://github.com/rll-research/B-Pref.

• background：
  • 强化学习（RL）需要使用激励正确 action 的 reward function，但众所周知，reward function 很难为复杂任务指定。
  • 基于偏好的 RL（PBRL）提供了一种替代方案：在没有预定义奖励的情况下，使用 teacher preference 来学习政策，从而克服了与奖励工程相关的问题。然而，由于缺乏普遍采用的基准，很难量化 PBRL 的进展。
• 工作：
  • 在本文中，我们介绍了 B-Pref，一个专门为 PBRL 设计的 benchmark。
  • 这种 benchmark 的一个关键挑战是，要对算法进行快速评估，所以，不能使用真实的人工输入，对 segment pairs 进行实时评估。同时，把 ground-truth reward function 拿来当作人类输入，这种完美 preference 也是不现实的。
  • B-Pref 模拟了具有广泛非理性（with a wide array of irrationalities）的 teacher，不仅提出了针对 performance 的指标，还提出了针对这些潜在非理性（irrationalities）的 robustness 指标。
• result：
  • 我们展示了 B-Pref 的实用性，使用它来分析最先进的 PBRL 算法设计，例如在 selecting informative queries 方面的设计。希望 B-Pref 可以作为系统研究 PBRL 的起点。
  • 源代码位于 https://github.com/rll-research/b-pref 。

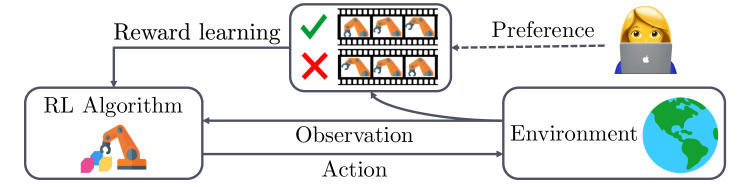
3 benchmarks environments for PBRL

• （section 3.2）建立了一个生成 preference 的 Stochastic preference model（随机偏好模型）：

  • \[P[σ^i\succ σ^j~;~β,γ]=\frac{\exp\big(β\sum_{t=1}^Hγ^{H-t}r(s^i_t,a^i_t)\big)} {\exp\big(β\sum_{t=1}^Hγ^{H-t}r(s^i_t,a^i_t)\big) + \exp\big(β\sum_{t=1}^Hγ^{H-t}r(s^j_t,a^j_t)\big)} \]

  • 若 β → ∞，则会得到 非零即一的 非常坚定的 P。β → 1 正常。γ 是 discount factor。

• 设计了几个 irrationalities：

  • Oracle（先知）：β → ∞。
  • Myopic behavior（短视）： discounted factor 变小。
  • Skipping queries（感觉不可比，跳过）：若 segment 的 reward 之和太小，则认为两个 segment 都没有做到预期行为，一样差，跳过。
  • Equally preferable（同样好，(0.5,0.5) ）：若两段 segment 的 reward 之和的差＜一个阈值，则返回 (0.5,0.5)。
  • Making a mistake（犯错，01 翻转）：概率为 ε。

• （section 3.3）metrics 评价指标：

  • 评价指标： trained agent 的 episodic return，使用 ground-truth reward function。
  • 评价 feedback-efficiency：改变 queries budget（预算）。大概就是改变 queries 的个数？
  • 评价 robustness：使用以下六个 teacher： oracle（β→∞）、stoc 随机（β→1）、错误（ε→0.1）、；skip 跳过、equal 同样好、myopic 短视。

• （section 3.4）tasks 任务：

  • DeepMind Control Suite （DMControl） 的两个 locomotion 任务（Walker-walk 和 Quadruped-walk）、Meta-world 的两个 robotic manipulation 任务（Button Press 和 Sweep Into）来自 （Yu 等人，2020 年）。
  • 专注于 ① 本体感受输入（proprioceptive inputs 而非 比如说 robotic arms + camera 的视觉输入 visual observations）② 密集奖励（dense reward 而非 sparse reward）。

4 algorithmic baselines for PBRL

大概是本文评测的 PBRL baselines？

• （section 4.1）PBRL 基础： reward model、preference、loss function。
• （section 4.2）PEBBLE：可以参考本站 博客。
  • 先通过基于熵（魔改）的 intrinsic reward，对 agent 进行 unsupervised pre-training；
  • 然后，在跑 PBRL 的过程中，选择熵最大（最接近 decision boundary）的 segment pair 进行 query；
  • 最后，在训 RL 时，每当 reward model 更新，就把所有之前得到的 transition tuple (s,a,s') 都重新标一下 r，重新训练。

5 使用 B-Pref 分析 PBRL 算法设计

Pieter Abbeel 的 experiment 部分之问：

• How do existing preference-based RL methods compare against each other across environments with different complexity?
  现有的 PBRL 方法，在不同复杂度的环境中，如何相互比较？
• How to use B-Pref to analyze algorithmic design decisions for preference-based RL?
  如何使用 B-Pref 分析 PBRL 的算法设计决策？

正文：

• （section 5.1）Training details：好像还涉及了一个算法 PrefPPO，好像还没了解过…

• （section 5.2）对 prior methods 进行 benchmarking，大概是“对现有方法进行基准测试”的意思？大概是实验结果。

• （section 5.3）算法设计对 reward learning 的影响：

• Selecting informative queries：首先考察 sampling queries 的方法：（详见 Appendix C）

  • uniform sampling 均匀采样。

  • uncertainty-based sampling 基于不确定性的采样：测量不确定性，使用 ensemble reward model 的方差，或熵的方差之类。

  • coverage-based sampling 基于覆盖率的采样： greedy method，选择与其最近 center 距离最大的 query；选择尽量远的，尽可能覆盖整个空间。

  • hybrid method：首先，使用基于不确定性的采样，选择 N_inter 个 segment pair，然后再在其中选择 N_query 个中心点。

  • 实验结果： uncertainty-based sampling 最好，coverage-based sampling 没有用还变慢了。

• Feedback schedule：

  • Feedback schedule：每个 feedback sessions 的 queries 数量。
  • ① uniform；② decay：正比于 T/(T+t)；③ increase：正比于 (T+t)/T。
  • 实验结果：感觉没什么影响。meta-gradient 这样的自适应 schedule 还是有趣的。

• Reward analysis：作者声称 PEBBLE 学到的 reward function 与 ground truth 是对齐的。

• misc：

  • 貌似 figure 2 使用的指标是 IQM（interquartile mean 四分位数间平均值），是一种平均值定义。figure 2 考察了 normalized episodic returns 的 IQM 平均值，normalize 方法见 section 3.3 的公式，PBRL average returns 除以使用 ground truth reward 的 RL 的 average returns。
  • Appendix 里有大量实验结果。

6 related work

• RL benchmark，感觉提到了很多有名的 benchmark。
• Human-in-the-loop RL。