title: 摄像机模型
banner_img: https://drive.studyinglover.com/api/raw/?path=/photos/blog/background/1679396994125.png
date: 2022-12-29 21:47:00
categories:
- 工具
tags:
- 机器视觉
摄像机模型
本文是鲁鹏老师机器视觉课程的笔记
针孔模型与透镜
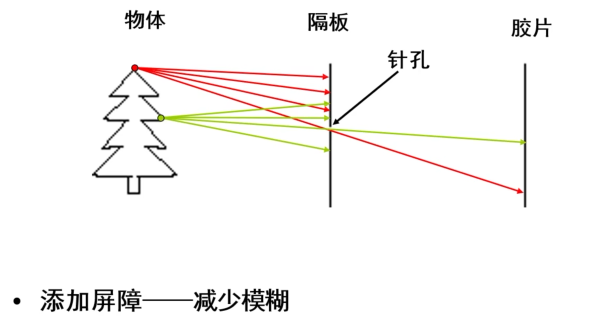
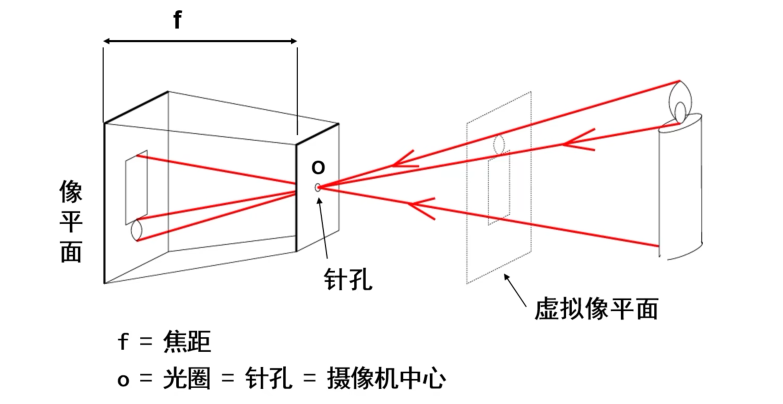
虚拟像平面是倒着的
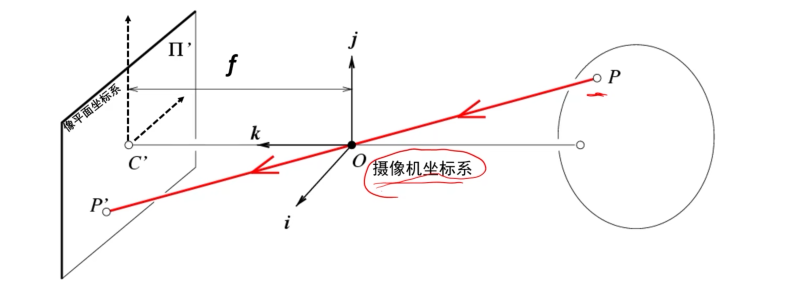
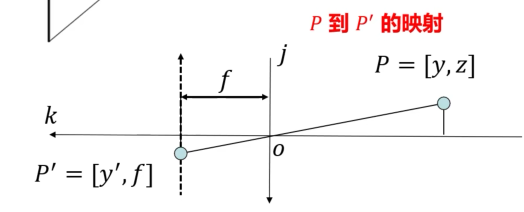
\(\dfrac{y'}{f}=\dfrac{y}{z}\quad\implies y'=f\dfrac{y}{z}\)
\(\dfrac{x'}{f}=\dfrac{x}{z}\quad\implies x'=f\dfrac{x}{z}\)
\(P=\begin{bmatrix}x\\ y\\ z\end{bmatrix}\to P'=\begin{bmatrix}x'\\ y'\end{bmatrix}\quad\quad\)
\(\begin{cases}x'=f\dfrac{x}{Z}\\ y'=f\dfrac{y}{Z}\end{cases}\)
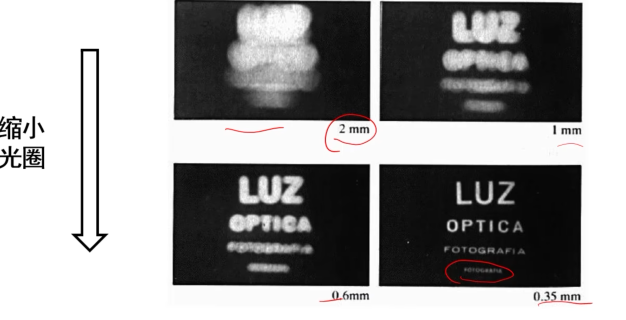
光圈尺寸
光圈偏大会导致场景模糊
光圈偏小会场景清晰,但偏暗
增加透镜
- 透镜将多条光线聚焦到胶片上,增加了照片的亮度:
- 所有平行于光轴的光线都会会聚到焦点,焦点到透镜中心的距离称为焦距
- 穿过中心的光线的方向不发生改变
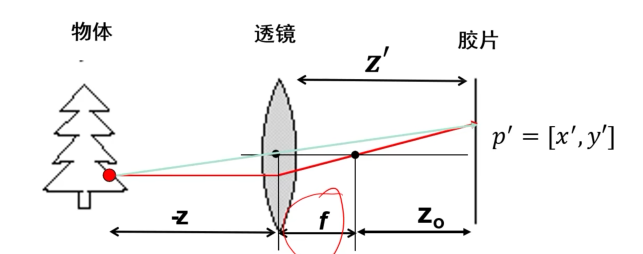
根据折射定律: \(f=\frac{ {R} }{ {2}({n}-1)}\) ,\(R\) 是透镜球面半径,\(n\)是透镜折射系数
\(z'=f+z_0\quad\begin{cases}x'=z'\dfrac{x}{z}\\ y'=z'\dfrac{y}{z}\end{cases}\)
要是透镜不合适,则会发生失焦
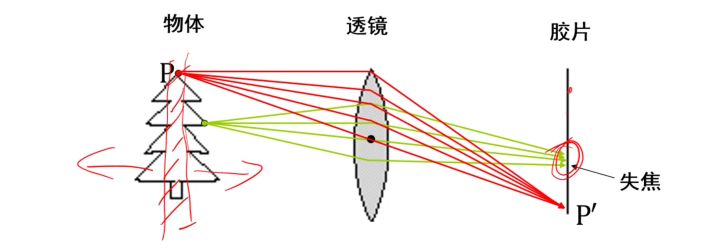
透镜将光线聚焦到胶片上
- 物体“聚焦”有特定距离
- 景深
径向畸变
图像中所成的像发生形变
径向畸变:图像像素点以畸变中心为中心点,沿着径向产生的位置偏差,从而导致

枕形畸变:畸变像点相对于理想像点沿径向向外偏移,远离中心
桶形畸变:畸变像点相对于理想点沿径向向中心靠拢
摄像机几何
齐次坐标
\(E\to H\)
图像点的齐次坐标\(\text{}(x,y)\Rightarrow\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\)
空间点的齐次坐标\((x,y,z)\Rightarrow\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\)
\(H \to E\)
\(\left[\begin{array}{c}x\\ y\\ w\end{array}\right]\Rightarrow\left(x/w,y/w\right)\)
\(\left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]\Rightarrow\left(x/w,y/w,z/w\right)\)
\(H \to E\) 的转变不是唯一的,但\(E \to H\) 的转变是唯一的
像素坐标系
建立像平面到像素平面关系
- 偏置
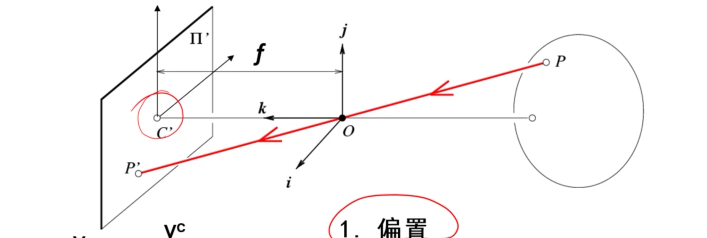
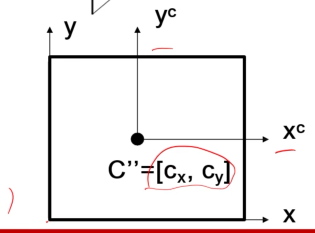
\((x,y,z)\to(f\dfrac{x}{z}+c_x,f\dfrac{y}{z}+c_y)\)
- 单位变换
\((x,y,z)\to({fk}\frac{x}{z}+c_x,{fl}\frac{y}{z}+c_y)\)
单位:k.l:pixel/m , f:m
k表示竖直方向上多少米表示一个像素,l表示水平方向上多少米表示一个像素
记\(fk\)为\(\alpha\) ,\(fl\)为\(\beta\)
\(P=(x,y,z)\rightarrow P^{\prime}=\left(\alpha{\frac{x}{z} }+c_{x},\beta{\frac{y}{z} }+c_{y}\right)\) ,这里的\(c_x,c_y\)是像素上的偏置
\(P=(x,y,z)\rightarrow P^{\prime}=\left(\alpha{\frac{x}{z} }+c_{x},\beta{\frac{y}{z} }+c_{y}\right)\)是非线性变换
在齐次坐标系下
\(P_h'=\begin{bmatrix}\alpha x+c_x z\\ \beta y+c_yz\\ z\end{bmatrix}=\begin{bmatrix}\alpha&0&c_x&0\\ 0&\beta&c_y&0\\ 0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}\)
\(P'_h\to P'=(\alpha\dfrac{x}{z}+c_x,\beta\dfrac{y}{z}+c_y)\)
\(P'_h\)是齐次,\(P'\) 是欧式
摄像机的投影矩阵
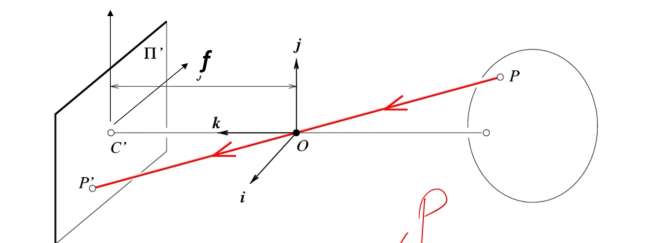
\(P'=\begin{bmatrix}\alpha&0&c_x&0\\ 0&\beta&c_y&0\\ 0&0&1&0\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}=MP\)
其中\(M=\begin{bmatrix}\alpha&-\alpha\cot\theta&c_x&0\\ 0&\dfrac{\beta}{sin\theta}&c_y&0\\ 0&0&1&0\end{bmatrix}\)
此时\(P\)和\(P'\) 是线性表示
\(P'\)是\(3*1\)矩阵,\(P\) 是\(4*1\)矩阵
摄像机偏斜
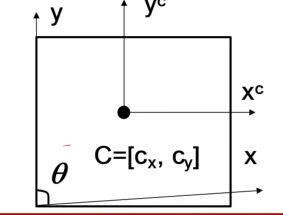
\(P'=\begin{bmatrix}\alpha&-\alpha\cot\theta&c_x&0\\ 0&\frac{\beta}{sin\theta}&c_y&0\\ 0&0&1&0\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}\)
摄像机坐标系下的摄像机模型
\(P'=\begin{bmatrix}\alpha&-\alpha\cot\theta&c_x&0\\ 0&\frac{\beta}{sin\theta}&c_y&0\\ 0&0&1&0\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}=MP\)
\(M=\begin{bmatrix}\alpha&-\alpha\cot\theta&c_x&0\\ 0&\frac{\beta}{sin\theta}&c_y&0\\ 0&0&1&0\end{bmatrix}\)被称为投影矩阵,
\(K=\begin{bmatrix}\alpha&-\alpha\cot\theta&c_x\\ 0&\frac{\beta}{sin\theta}&c_y\\ 0&0&1\end{bmatrix}\) 被称为摄像机内参数矩阵,内参数矩阵决定了摄像机坐标系下空间点到图像点的映射
摄像机内参数为\(\alpha,\beta,c_x,c_y,\theta\),K有五个自由度
规范化投影变换
\(P'=\begin{bmatrix}x\\ y\\ z\end{bmatrix}=\begin{bmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\end{bmatrix}\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}\)
已知摄像机矩阵\(M\) , \(P'=I(MP)\),\(I=\begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix}\)
\(\begin{array}{c}\Re^4\xrightarrow{H}\Re^3\\ \boldsymbol{P'}=M\boldsymbol{P}\end{array}\)
\(P\) 的欧式坐标\(\left[\begin{array}{c}{ {\frac{x}{z} }}\\ { {\frac{y}{z} }}\\ \end{array}\right]\)
世界坐标系
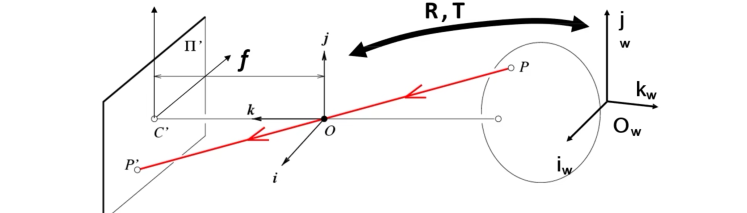
\(O_w\) 为世界坐标系 \(O\)摄像机坐标系,\(C'\)像平面坐标系
齐次坐标系\(P=\left[\begin{matrix}{R}&{T}\\ {0}&{1}\\ \end{matrix}\right]\boldsymbol{P}_{w}\) , \(\begin{bmatrix}x_w\\ y_w\\ z_w\\ 1\end{bmatrix}\) ,即摄像机坐标系是世界坐标系经过一个旋转,再经过一个平移得到的
世界坐标系下\(P_w=R^T(P-T)\)
从世界坐标系到像素坐标系\(P'=K[I\quad0]P=K[I\quad0]\begin{bmatrix}R&T\\ 0&1\end{bmatrix}P_w=K[R\quad T]P_w=MP_w=\left[{\begin{matrix}{m_{1} }\\ {m_{2} }\\ {m_{3} }\end{matrix} }\right]P_{\mathrm{w} }\)
\(\begin{bmatrix}R & T\end{bmatrix}\)称为外参数矩阵,K是内参数,这就是完整的摄像机模型
\(M\) 称为投影矩阵,有11个自由度
摄像机O点坐标为\(-R^TT\)
\(\left[{\begin{matrix}{m_{1} }\\ {m_{2} }\\ {m_{3} }\end{matrix} }\right]P_{\mathrm{w} }\) 是转换为欧式坐标系的写法,\(m_i\) 是一个\(1*4\) 的矩阵

投影变化的性质
- 点投影为点
- 线投影为线
- 近大远小
- 角度不再保持
- 平行线相交
其他摄像机模型
透视投影摄像机
^b240bc
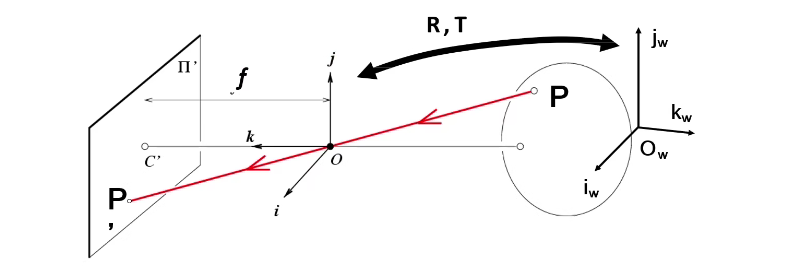
\(P'_{3\times1}=MP_W=K_{3\times3}[R\quad T]_{3\times4}P_{W4\times1}=\begin{bmatrix}m_1\\ m_2\\ m_3\end{bmatrix}P_w=\begin{bmatrix}m_1P_w\\ m_2P_w\\ m_3P_w\end{bmatrix}\stackrel{E}{\longrightarrow}(\dfrac{m_1P_w}{m_3P_w},\dfrac{m_2P_w}{m_3P_w})\quad,M=\begin{bmatrix}m_1\\ m_2\\ m_3\end{bmatrix}\)
弱透视投影摄像机
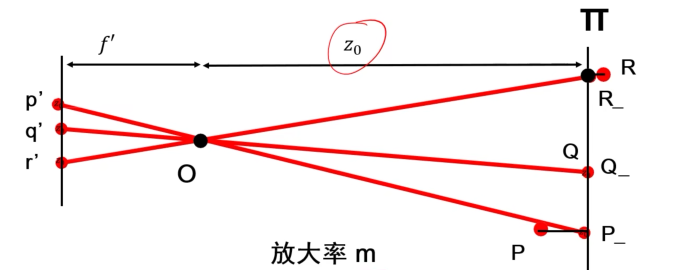
\(\begin{cases}x'=\dfrac{f'}{z}x\\ y'=\dfrac{f'}{z}y\end{cases}\rightarrow\begin{cases}x'=\dfrac{f'}{z_0}x\\ y'=\dfrac{f}{z_0}y\end{cases}\)
从投影(透视)到弱透视\(M=K[RT]=\begin{bmatrix}A_{2\times3}&b_{2\times1}\\ v_{1\times2}&1\end{bmatrix}\quad\to M=\begin{bmatrix}A&b\\ 0&1\end{bmatrix}\quad\)
\(P'=MP_w=\begin{bmatrix}m_1\\ m_2\\ m_3\end{bmatrix}P_w=\begin{bmatrix}m_1P_w\\ m_2P_w\\ 1\end{bmatrix}\stackrel{E}{\longrightarrow}\left(m_{1}P_{W},m_{2}P_{w}\right)\) ,\(m_1,m_2\) 为放大率
\(M=\begin{bmatrix}A&b\\ v&1\end{bmatrix}=\begin{bmatrix}m_1\\ m_2\\ m_3\end{bmatrix}=\begin{bmatrix}&m_1&\\ &m_2&\\ 0&0&0&1\end{bmatrix}\)
正交投影摄像机
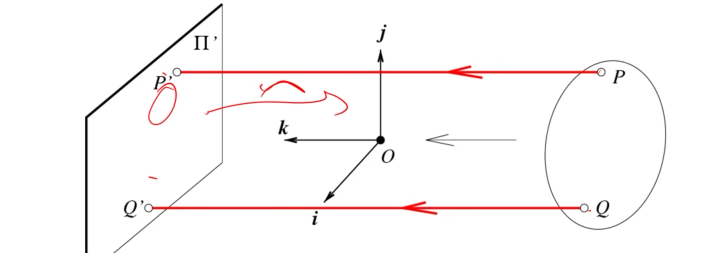
\(\begin{cases}x'=\dfrac{f'}{z}x\\ y'=\dfrac{f'}{z}y\end{cases}\quad\to\quad\begin{cases}x'=x\\ y'=y\end{cases}\)
各种摄像机模型的应用场合
- 正交投影
- 更多应用在建筑设计(AUTOCAD)或者工业设计行业
- 弱透视投影在数学方面更简单
- 当物体较小且较远时准确,常用于图像识别任务
- 透视投影对于3D到2D映射的建模更为准确
- 用于运动恢复结构或SLAM