题解
前言
个人认为官方题解写得最为详细、干净、清楚,如果有意向阅读外文版的题解的话,还是推荐去读一读:
Editorial - AtCoder Regular Contest 117
本文属于转载(?),有一些自己的思考过程,希望有帮助。
题意
有多少个长度为 \(2N\) 的序列 \(A\) 满足:
- 序列\(A\) 包含 \(N\) 个 \(+1\) 和 \(N\) 个 \(-1\)。
- 刚好有 \(K\) 对下标 \(l,r(1\leq l<r\leq 2N)\),满足 \(\sum\limits_{i=l}^{r} = 0\),我们把形如 \([l,r]\) 这样的区间称为“零和区间”。
给出 \(N,K\),求满足条件的序列个数。
\(1\leq N\leq 30,1\leq K\leq N^2\)。
分析
Part 1
我们考虑用最暴力的做法,那就是二进制枚举 \(A\) 的状态。然后枚举 \(l,r\) 采用前缀和相减判断是否为零和区间。
时间复杂度:\(O(2^n)\),预计:34 pts。
Part 2
显然 Part 1 的做法超时,那我们能不能得到一些启发呢?
显然是前缀和。
我们期望得到的是 \(sum_r-sum_{l-1}=0\),实际上,我们也就是想得到 \(sum_r=sum_{l-1}\)。由于原数组为 \(\pm 1\),所以当我们把前缀和数组看做是关于 \(i\) 的函数 \(sum_i\) 的话,得到的图像,必定是每一段都为 45° 的折线图。而起点与终点都将是 \(0\)。
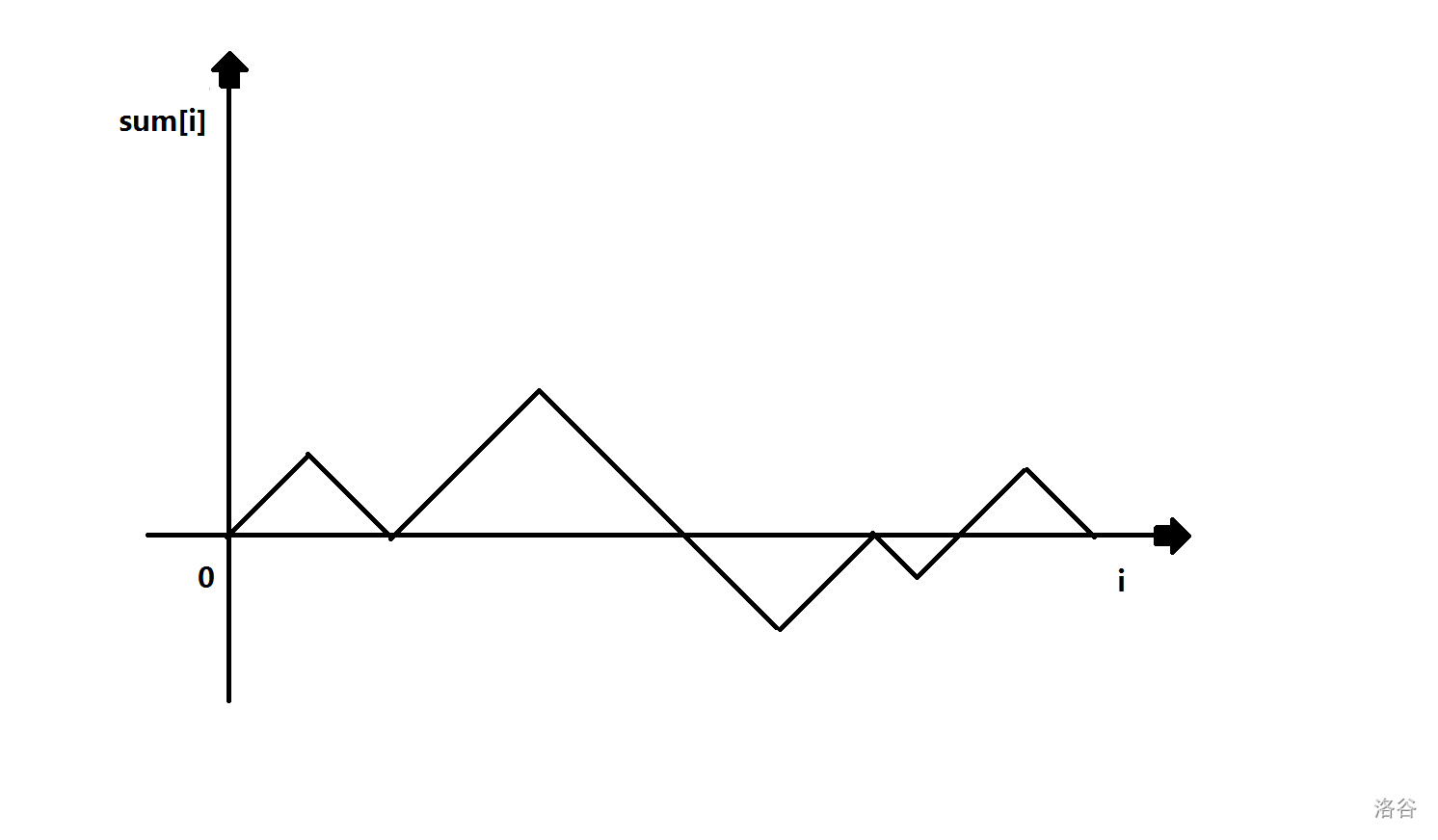
我们可以想象一条 \(y=k\) 的一条横线从上往下扫。我们就可以分别考虑放置所有二维平面上的点了。
我们发现两个相等且“相邻”的元素之前是可以放下一个或多个更小的元素的。“相邻”怎么解释?“相邻”代表着当只考虑当前的元素 \(y\) 与大于 \(y\) 的元素时,如果两个元素 \(y\) 之间没有再多一个元素 时,则称之为“相邻”。我们把“相邻”的元素之间的空隙,称之为“洞”。
如果考虑到当前这个“洞”(下文不再加括号),我们先考虑当前要放的元素都是相同的值。
那就可以自然地想到采用 dp。
设 \(f[x][y][z]\) 表示放了 \(x\) 个元素,得到了 \(y\) 个零和区间,还有 \(z\) 个洞的方案数。
如何转移?设当前放进洞里的元素数量为 \(p\),则转移方程为:
\[f[x][y][z]\to f[x+p][y+C_p^2][p-(z+2)] \]\[\Downarrow \]\[f[x][y][z]\to f[x+p][y+\frac{p\times(p-1)}{2}][p-(z+2)] \]为什么剩下的洞的数量是 \(p-(z+2)\) 呢?因为原来有 \(z\) 个洞,每个洞需要放一个元素,同时最左边与最右边又需要各放一个元素,就共放了 \(z+2\) 个元素。
在此基础上,每多放一个元素,就可以多增加一个洞。自然就是 \(p-(z+2)\)。
值得一提的是,上式并没有采用等号连接,因为方程还需要再乘上一个 \(C_{p-1}^{z+1}\)(读者自证)。所以方程应该是这样:
设 \(x'=x+p,y'=y+\frac{p(p-1)}{2},z'=p-(z+2)\),则
\[f[x'][y'][z']=\sum\limits_{x,y,z} f[x][y][z]\times C_{p-1}^{z+1} \]最后答案需要记录 \(x\) 轴上、下方的贡献,总共就是
\[ans=\sum\limits_{x,y,z} f[x][y][z]\times f[2n-x][k-y][z-1] \]至于为什么是 \(z-1\) 呢?这个显然,请读者联系一下上图思考。(提示,\(x\) 轴下方可以翻转过来相似地考虑。)
到这里就结束了,可以开码了。
时空复杂度:\(O(n^5)\),预计:100 pts。
代码
马蜂有点抽象,将就看看吧(
code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN = 60 + 5, MAXM = 1800 + 5;
int n, m;
int f[MAXN][MAXM][MAXN];
int ans;
int c[2 * MAXN + 5][2 * MAXN + 5];
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 0; i <= 2 * n; i++) {
c[i][0] = 1;
for (int j = 1; j <= i; j++) {
if (j != i)
c[i][j] += c[i - 1][j];
c[i][j] += c[i - 1][j - 1];
}
}
for (int i = 1; i <= n + 1 && i * (i - 1) / 2 <= m; i++) f[i][i * (i - 1) / 2][i - 1] = 1;
for (int i = 1; i <= 2 * n + 1; i++) {
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (f[i][j][k] == 0)
continue;
for (int p = k + 2; i + p <= 2 * n + 1 && p <= n + 1; p++) {
if (j + p * (p - 1) / 2 > m)
break;
f[i + p][j + p * (p - 1) / 2][p - (k + 2)] += f[i][j][k] * c[p - 1][k + 1];
}
}
}
}
ans = f[2 * n + 1][m][0];
for (int i = 0; i <= 2 * n + 1; i++) {
for (int j = 0; j <= m; j++) {
for (int k = 1; k <= n; k++) {
ans += f[i][j][k] * f[2 * n + 1 - i][m - j][k - 1];
}
}
}
printf("%lld\n", ans);
return 0;
}