Link

CF1898 D Absolute Beauty

Question

给出两个长度都为 \(n\) 的数组 \(a,b\) ，我们可以任意选择两个数 \(i,j\) 交换 \(b_i\) 和 \(b_j\) 一次，或者不换

求 \(\sum\limits_{i=1}^n |a_i-b_i|\) 的最大值

Solution

把一个 \(a_i,b_i\) 抽象成一条线段

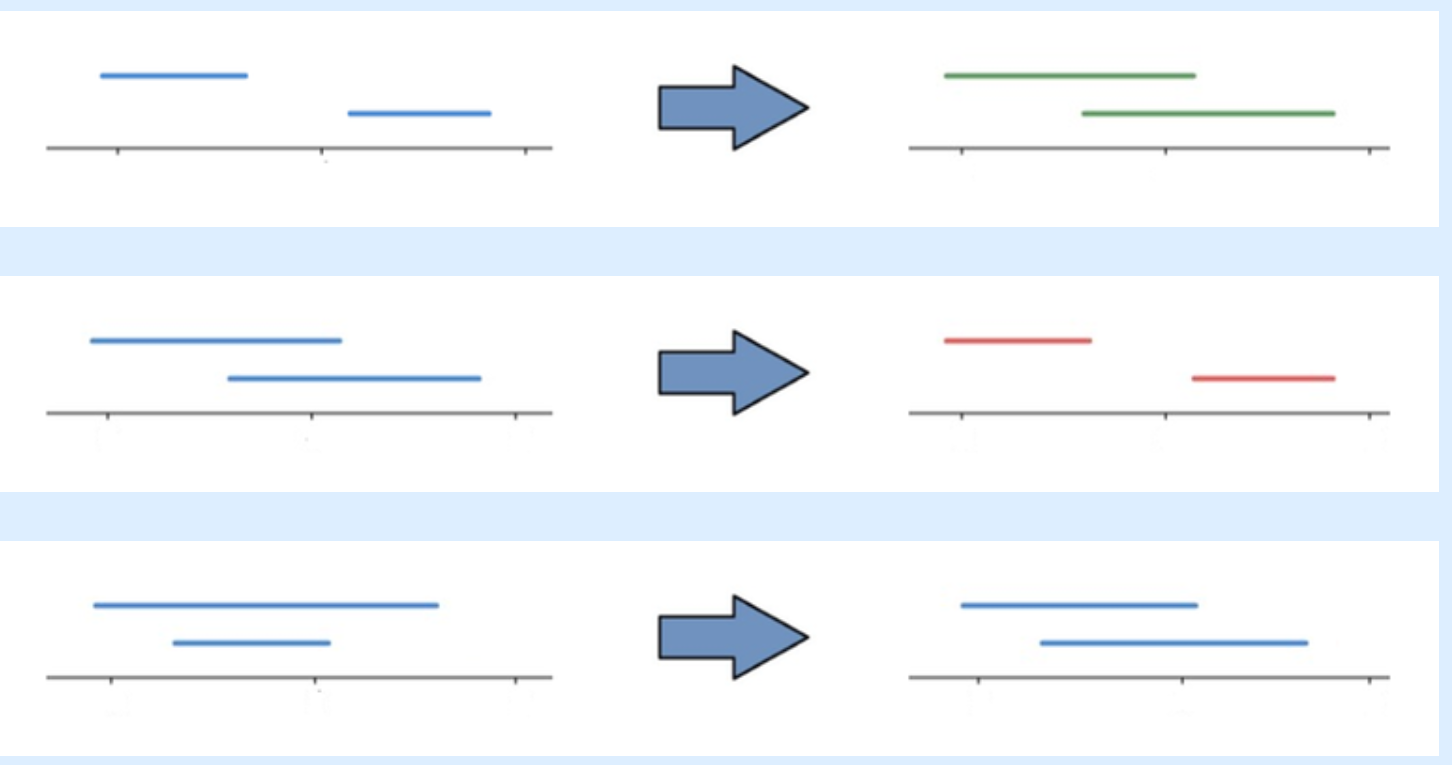
而交换 \(b\) 的操作可以视为交换两个线段的端点

我们发现了一个有趣的性质，就是 \(a_i,b_i\) 可以任意表示左端点或右端点，也就是说，\(a_i,b_i\) 可以随意调换，对这个题的答案没有影响

通过图片可以观察出，第二种情况下，覆盖长度增加了两倍中间的值，也就是说，我们只需要找到最小的右端点和最大的左端点，交换他们就是答案

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=2e5+5;
const LL INF=1ll<<60;
inline int read(){
    int ret=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
    while(ch<='9'&&ch>='0')ret=ret*10+ch-'0',ch=getchar();
    return ret*f;
}
struct Line{
    LL L,R;
}L[maxn];
inline void solve(){
    int N=read();
    LL ans=0;
    for(int i=1;i<=N;i++) L[i].L=read();
    for(int i=1;i<=N;i++) L[i].R=read();
    for(int i=1;i<=N;i++) {
        if(L[i].L>L[i].R) swap(L[i].L,L[i].R);
        ans+=L[i].R-L[i].L;
    }
    LL MaxL=-INF,MinR=INF;
    for(int i=1;i<=N;i++){
        MaxL=max(MaxL,L[i].L);
        MinR=min(MinR,L[i].R);
    }
    printf("%lld\n",ans+max((MaxL-MinR)*2,0ll));
    return ;
}
int main(){
    // freopen("D.in","r",stdin);
    // freopen("D.out","w",stdout);
    int T=read();
    while(T--)solve();
    return 0;
}

Summary

• 对于绝对值函数，可以抽象成线段