Link

CF1898 C Colorful Grid

Question

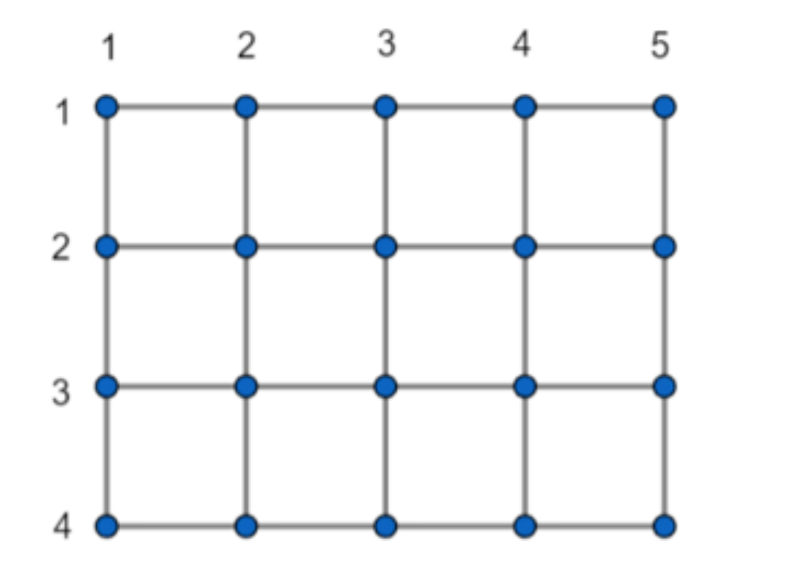
给出一个 \(N\times M\) 的网格图

给每一条边染色(R/B)，需要存在一条长度为 \(K\) 的路径从 \((1,1)\) 到 \((N,M)\)，路径允许重复通过一个节点。

Solution

非常有意思的一道题

先考虑 \(K\) 满足的最小值，显然是 \((N-1)+(M-1)\) ，假设走 上->左 这样的路径

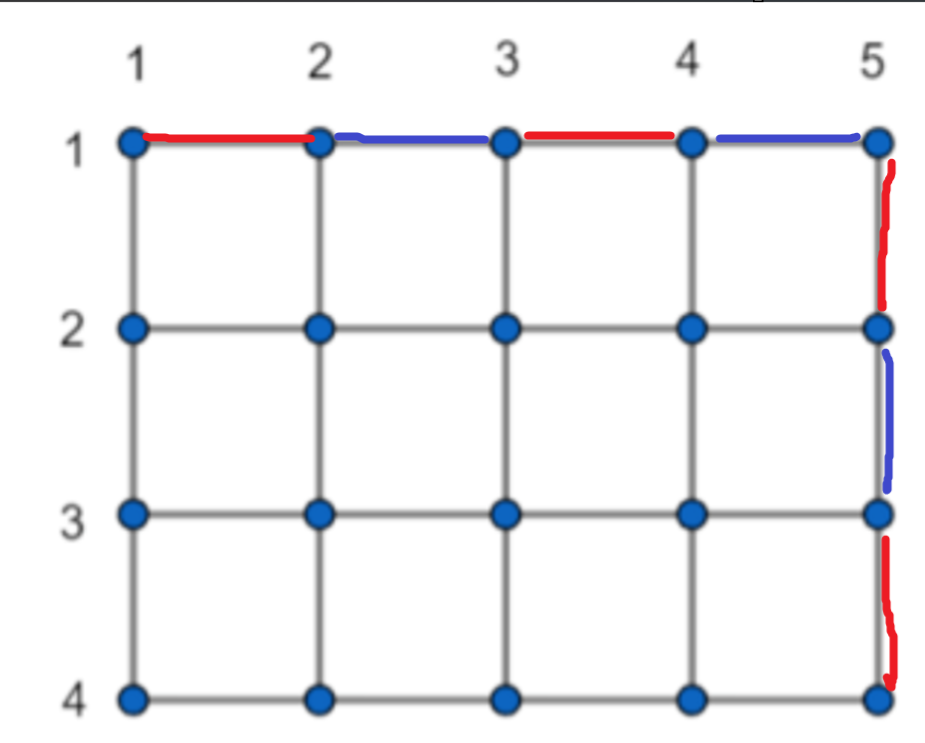
接着思考其他可行的 \(K\) 值，当到终点后，顺着一个格子转几圈显然也成立，所以对于一个可行的 \(K\)， \(K+4c\) 也可行，\(c\) 为任意整数

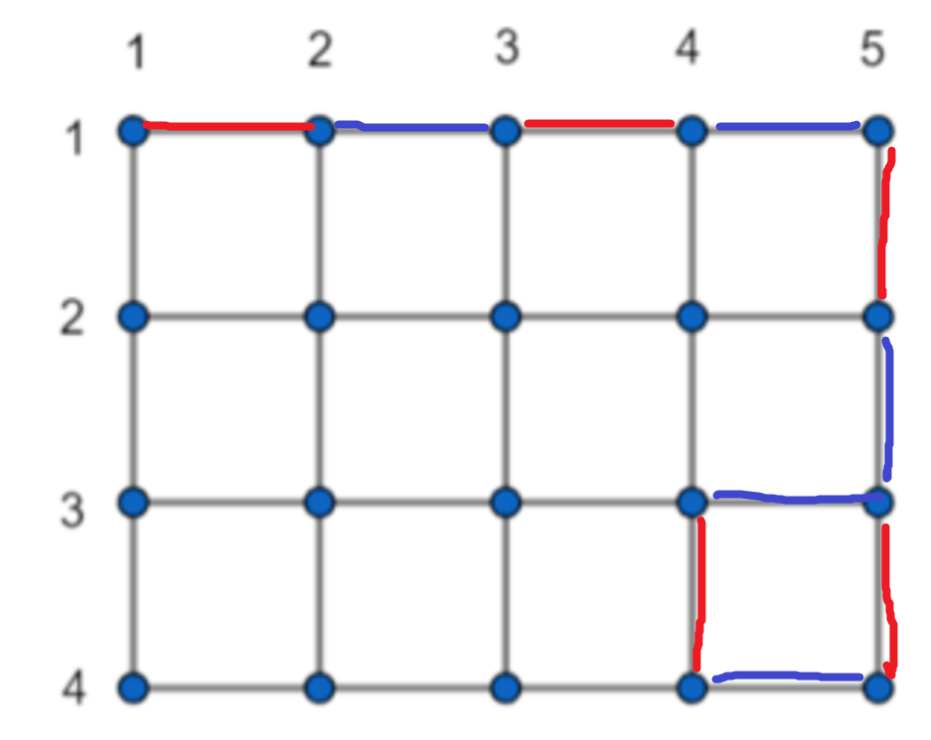
当走在一条直线上，往下走一步，又往上走一步，显然也是成立的，所以对于一个可行的 \(K\) ，\(K+2\) 也成立

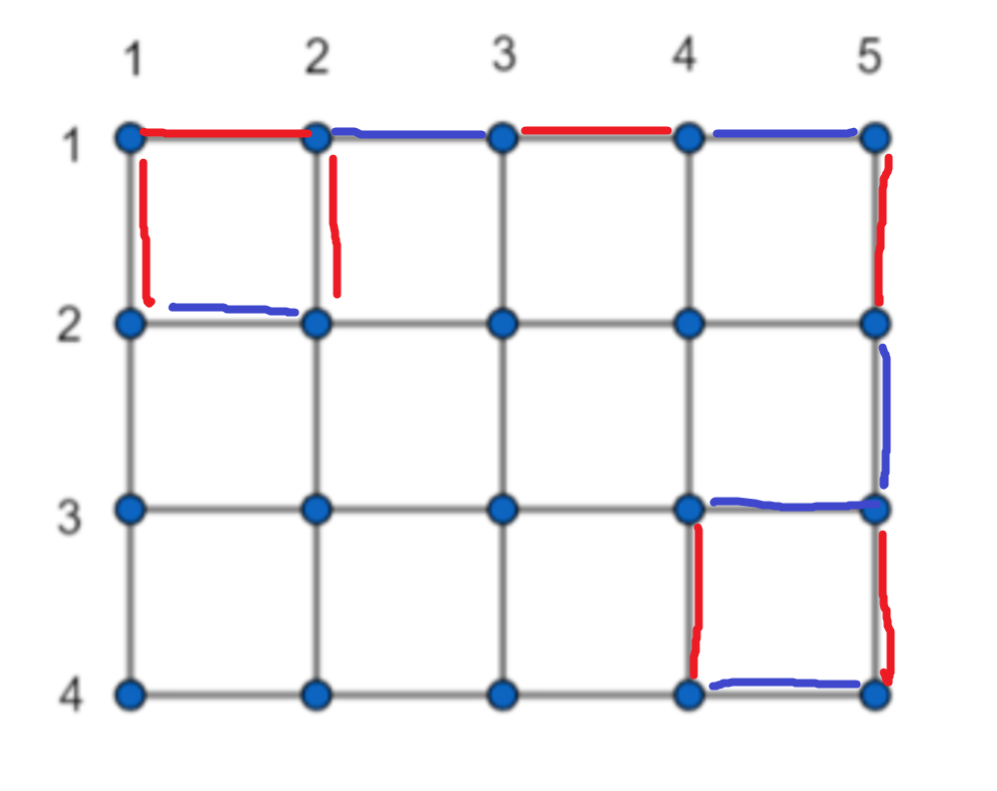
综上，\(K\%((N-1)+(M-1))\) 为 \(0\) 和 \(2\) 时 是 YES 。

Code

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int ret=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
    while(ch<='9'&&ch>='0')ret=ret*10+ch-'0',ch=getchar();
    return ret*f;
}
const int maxn=20;

void solve(){
    int N=read(),M=read(),K=read();
    int lst=K-(N-1)-(M-1);
    if(lst<0||(lst%4!=0&&lst%4!=2)) {printf("NO\n");return;}
    int L[maxn][maxn]={0},C[maxn][maxn]={0};
    int tim=0;
    for(int i=1;i<M;i++) 
        {L[1][i]=tim,tim^=1;}    
    for(int j=1;j<N;j++) 
        {C[j][M]=tim,tim^=1;}
    L[N][M-1]=tim,tim^=1;
    C[N-1][M-1]=tim,tim^=1;
    L[N-1][M-1]=tim,tim^=1;

    tim=0;
    C[1][1]=tim,tim^=1;
    L[2][1]=tim,tim^=1;
    C[1][2]=tim,tim^=1;
    printf("YES\n");
    for(int i=1;i<=N;i++){
        for(int j=1;j<M;j++) printf("%c ",L[i][j]?'B':'R');
        printf("\n");
    }
    for(int i=1;i<N;i++){
        for(int j=1;j<=M;j++) printf("%c ",C[i][j]?'B':'R');
        printf("\n");
    }
}
int main(){
    // freopen("C.in","r",stdin);
    // freopen("C.out","w",stdout);
    int T=read();
    while(T--) solve();
    return 0;
}