Link

CF1899 G Unusual Entertainment

Question

给出一个排列 \(p_i\) 和一棵树，给出 \(Q\) 组询问，每组询问 \([L,R,x]\) 表示求 \(p_L \sim p_R\) 上是否存在 \(p_i\) 在 \(x\) 的字数上。

Solution

这道题确实是一个好题。

我们先考虑一个问题，怎么样才能判断子树，我们给书上的每个节点建立两个时间戳 \(tin[x],tou[x]\) ，对于两个节点 \(u,v\) 如果 \(u\) 在 \(v\) 的子树上，满足 \(tin[v] \le tin[u] \le tou[v]\)。

那么我们设 \(a_i=tin[p_i]\) ，那么这个问题就转化为在 \(a_L \sim a_R\) 上，是否存在一个 \(a_i\) 在 \([tin_x,tou_x]\) 上。

接下来考虑如何解决这个转化以后的问题，观察到 \(p_i\) 是无序的，如果 \(p_i\) 是有序的，那么这个问题就很简单了。

假设 p 数组为 2,5,7,10 ，\(tin_x\) 为 9 \(tou_x\) 为 11，那么使用差分的思想，在 p 数组内二分 \(tin_x\) 和 \(tou_x\) 的位置，如果位置不相同，说明 p 数组中有一个数 \(p_i\) 满足 \(tin_x \le p_i \le tout_x\)，并且，这种方法能让我们得出有几个数满足这个条件。

那么如何让 p 数组有序呢，可以使用归并树，类似于线段树的思想，只不过每个节点都记录了对应排序好的值，例如，当前节点的区间为 \([l,r]\)，那么就可以用一个 vector<int> 来记录 \([l,r]\) 排序好的值，在向上更新的时候归并排序就好了。

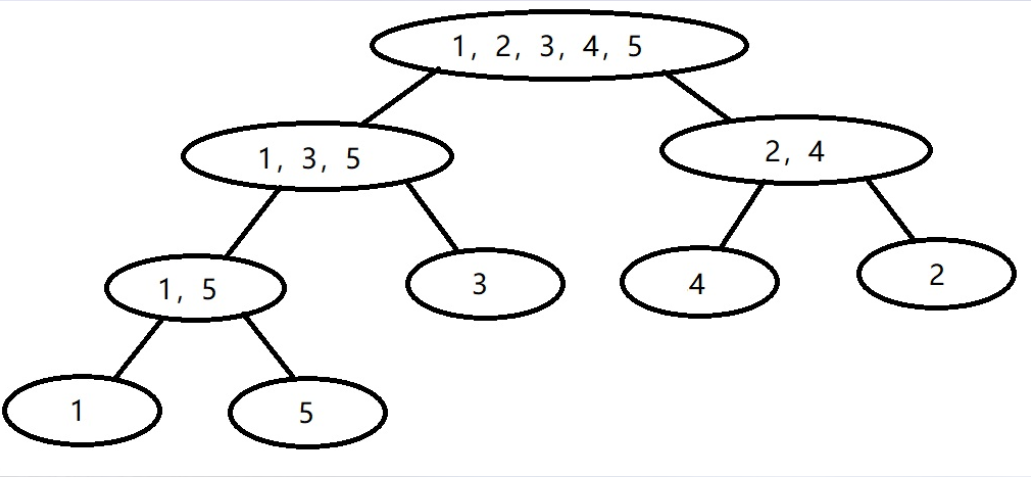
类似于线段树的思想，每一个询问区间 \([L,R]\) 最多被分成 \(log_2N\) 个小区间，然后各个小区间里面二分求解，所以总的时间复杂度是 \(O(Qlog^2N)\)。

Code

#include <bits/stdc++.h>
 
using namespace std;
 
#define sz(x) (int)x.size()
#define all(x) x.begin(), x.end()
 
struct SegmentTree {
    int n;
    vector<vector<int>> tree;
 
    void build(vector<int> &a, int x, int l, int r) {
        if (l + 1 == r) {
            tree[x] = {a[l]};
            return;
        }
 
        int m = (l + r) / 2;
        build(a, 2 * x + 1, l, m);
        build(a, 2 * x + 2, m, r);
        merge(all(tree[2 * x + 1]), all(tree[2 * x + 2]), back_inserter(tree[x]));
    }
 
    SegmentTree(vector<int>& a) : n(a.size()) {
        int SIZE = 1 << (__lg(n) + bool(__builtin_popcount(n) - 1));
        tree.resize(2 * SIZE - 1);
        build(a, 0, 0, n);
    }
 
    int count(int lq, int rq, int mn, int mx, int x, int l, int r) {
        if (rq <= l || r <= lq) return 0;
        if (lq <= l && r <= rq) return lower_bound(all(tree[x]), mx) - lower_bound(all(tree[x]), mn);
 
        int m = (l + r) / 2;
        int a = count(lq, rq, mn, mx, 2 * x + 1, l, m);
        int b = count(lq, rq, mn, mx, 2 * x + 2, m, r);
        return a + b;
    }
 
    int count(int lq, int rq, int mn, int mx) {
        return count(lq, rq, mn, mx, 0, 0, n);
    }
};
 
vector<vector<int>> g;
 
vector<int> tin, tout;
int timer;
void dfs(int v, int p) {
    tin[v] = timer++;
    for (auto u : g[v]) {
        if (u != p) {
            dfs(u, v);
        }
    }
    tout[v] = timer;
}
 
void solve() {
    int n, q;
    cin >> n >> q;
    
    g.assign(n, vector<int>());
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--; v--;
        g[u].push_back(v);
        g[v].push_back(u);
    }
 
    timer = 0;
    tin.resize(n);
    tout.resize(n);
    dfs(0, -1);
    
    vector<int> p(n);
    for (int i = 0; i < n; i++) cin >> p[i];
 
    vector<int> a(n);
    for (int i = 0; i < n; i++) a[i] = tin[p[i] - 1];
    SegmentTree ST(a);
 
    for (int i = 0; i < q; i++) {
        int l, r, x;
        cin >> l >> r >> x;
        l--; x--;
        if (ST.count(l, r, tin[x], tout[x])) {
            cout << "YES\n";
        } else {
            cout << "NO\n";
        }
    }
}
 
int main() {
    int tests;
    cin >> tests;
    while (tests--) {
        solve();
        if(tests > 0) cout << "\n";
    }
    return 0;
}