首页 > 其他分享 >2023年11月第一周题解-------数组

2023年11月第一周题解-------数组

时间：2023-11-05 19:22:04浏览次数：25  
标签：11 ------- int 题解 high ++ low include swap

1. 问题A：LY学长的随机数

解题思路

第一种思路是先去重后排序

第二种思路是先排序再去重

解题方法

暴力遍历

#define  _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#define N 10

void quickSort(int *a, int low, int high);//快速排序 
void swap(int *a, int low, int high);//交换a[low]和a[high]的值 
int* partition(int *a, int low, int high);//把a中low到high的数分类，小于的在左边，等于的在中间，大于的在右边 
int rm(int* nums, int numsSize){//给数组去重
    int k=numsSize,i,j,m;
 
    for(i=0;i<k;i++)
    {
        for(j=i+1;j<k;j++)
        if(nums[i]==nums[j])
        {
            for(m=j+1;m<k;m++)
            {
                nums[m-1]=nums[m];
            }
            k--;
            j=i;
        }
    }
    return k;
}

int main() {
    int n = 0;
    
    scanf("%d", &n);
    
    int *p = (int*)malloc(sizeof(int) * n);
    
    for (int i = 0; i < n; i++) {
        scanf("%d", p + i);
    }
    
    int size = 0;
    
    size = rm(p, n);//O(N^3)
    
    quickSort(p, 0, size - 1);//O(Nlog(N))
    
    printf("%d\n", size);
    
    for(int i = 0; i < size; i++) {
        printf("%d ", p[i]);
    }

    return 0;
}
void quickSort(int *a, int low, int high)
{
	int *p = NULL;//存储等于基准值的左右边界 
	
	if ( low >= high) {//如果只有一个值不用排序就直接结束排序 
		return ;
	}
	
	swap(a, low + rand() % (high - low + 1), high);
	p = partition(a, low, high);
	quickSort(a, low, p[0] - 1);
	quickSort(a, p[1] + 1, high);
	free(p);
}
void swap(int *a, int low, int high)
{
	int t = 0;
	
	t = a[low];
	a[low] = a[high];
	a[high] = t;
}
int* partition(int *a, int low, int high)
{
	int l = low - 1;
	int r = high;
	int i = low;
	int key = a[high];
	while(i < r) {
		if (a[i] < key) {
			swap(a, l + 1, i);
			i++;
			l++;
		}
		else  if ( a[i] > key){
			swap(a, r - 1, i);
			r--;
		}
		else {
			i++;
		}
	}
	swap(a, r, high);
	int *p = (int *)malloc(sizeof(int ) * 2);
	p[0] = l + 1;
	p[1] = r;
	return p;
}

暴力的去找数组中相同的数，找到了就从数组中删除。看rm函数我们可以发现这个方法的时间复杂度为O(N3),复杂度太高了，那么我们思考可不可以优化呢很明显是可以的。

双指针

#define  _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#define N 10

void quickSort(int *a, int low, int high);//快速排序 
void swap(int *a, int low, int high);//交换a[low]和a[high]的值 
int* partition(int *a, int low, int high);//把a中low到high的数分类，小于的在左边，等于的在中间，大于的在右边 
int rm(int* nums, int target, int numsSize){//去重O(N)
	int i, j;//双指针
    for (i = 0, j = 0; i < numsSize; i++){
    	if (nums[i] != target) {
    		nums[j++] = nums[i];
		}
	}
	nums[j] = target;//再把这个数赋值到数组的最后
	
	return j + 1;//返回去重后的数组长度
}

int main() {
    int n;
    
    scanf("%d", &n);
    
    int *p = (int*)malloc(sizeof(int) * n);
    
    for (int i = 0; i < n; i++)
    {
    	scanf("%d", p + i);
	}
	
	int size = n;
	
	for (int i = size - 1; i >= 0; i--) {//O(N)
		size = rm(p, p[i], size);//O(N^2)
	}
	
	quickSort(p, 0, size - 1);//O(NlogN)
	
	printf("%d\n", size);
	
	for (int i = 0; i < size; i++) {
		printf("%d ", p[i]);
	}
	
    return 0;
}
void quickSort(int *a, int low, int high)
{
	int *p = NULL;//存储等于基准值的左右边界 
	
	if ( low >= high) {//如果只有一个值不用排序就直接结束排序 
		return ;
	}
	
	swap(a, low + rand() % (high - low + 1), high);
	p = partition(a, low, high);
	quickSort(a, low, p[0] - 1);
	quickSort(a, p[1] + 1, high);
	free(p);
}
void swap(int *a, int low, int high)
{
	int t = 0;
	
	t = a[low];
	a[low] = a[high];
	a[high] = t;
}
int* partition(int *a, int low, int high)
{
	int l = low - 1;
	int r = high;
	int i = low;
	int key = a[high];
	while(i < r) {
		if (a[i] < key) {
			swap(a, l + 1, i);
			i++;
			l++;
		}
		else  if ( a[i] > key){
			swap(a, r - 1, i);
			r--;
		}
		else {
			i++;
		}
	}
	swap(a, r, high);
	int *p = (int *)malloc(sizeof(int ) * 2);
	p[0] = l + 1;
	p[1] = r;
	return p;
}

这个方法本质是对去重函数的优化，让去重函数的时间复杂度降低到了O(N),所以这个算法的时间复杂度是O(N2)，还是太高了，那么还可不可以优化到O(N)呢？

哈希表

#define  _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#define N 10

void quickSort(int *a, int low, int high);//快速排序 
void swap(int *a, int low, int high);//交换a[low]和a[high]的值 
int* partition(int *a, int low, int high);//把a中low到high的数分类，小于的在左边，等于的在中间，大于的在右边 

int main() {
    int n;
    int hash[10000] = {0};
    int m = 0;
    
    scanf("%d", &n);
    
    int *p = (int*)malloc(sizeof(int) * n);
    
    for (int i = 0; i < n; i++)
    {
    	int t = 0;
    	scanf("%d", &t);
    	if (hash[t] == 0) {//如果是0代表不在哈希表中，是第一次出现放进数组中
    		p[m++] = t;
		}
    	hash[t]++;
	}
	
	int size = m;
	
	quickSort(p, 0, size - 1);//O(NlogN)
	
	printf("%d\n", size);
	
	for (int i = 0; i < size; i++) {
		printf("%d ", p[i]);
	}
	
    return 0;
}
void quickSort(int *a, int low, int high)
{
	int *p = NULL;//存储等于基准值的左右边界 
	
	if ( low >= high) {//如果只有一个值不用排序就直接结束排序 
		return ;
	}
	
	swap(a, low + rand() % (high - low + 1), high);
	p = partition(a, low, high);
	quickSort(a, low, p[0] - 1);
	quickSort(a, p[1] + 1, high);
	free(p);
}
void swap(int *a, int low, int high)
{
	int t = 0;
	
	t = a[low];
	a[low] = a[high];
	a[high] = t;
}
int* partition(int *a, int low, int high)
{
	int l = low - 1;
	int r = high;
	int i = low;
	int key = a[high];
	while(i < r) {
		if (a[i] < key) {
			swap(a, l + 1, i);
			i++;
			l++;
		}
		else  if ( a[i] > key){
			swap(a, r - 1, i);
			r--;
		}
		else {
			i++;
		}
	}
	swap(a, r, high);
	int *p = (int *)malloc(sizeof(int ) * 2);
	p[0] = l + 1;
	p[1] = r;
	return p;
}

利用哈希表来帮我们去重，每次输入就判断key有没有再哈希表中，如果输入的数在哈希表中代表是重复的数，因此不把它放进我们的数组中。这样当输入结束时我们数组中的数一定是没有重复的。那么我们就只要排序了。这样我们的时间复杂度O(NlogN)就已经很好了。当然这个哈希表的实现不是很聪明，如果数据大了就不行。

2. 问题B：开灯问题

解题思路

  1. 用一个数组来模拟灯的状态
  2. 刚开始灯都是关着的
  3. 让每个人去关他对应的灯
  4. 当所有人都做完的时候
  5. 检查还有那些灯开着，并打印

解题方法

从人的角度出发

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#include <stdbool.h>

int main(int argc,char *argv[])
{
   int n =  0, k = 0;
   
   scanf("%d%d", &n, &k);//n代表有几盏灯，k代表有几个人 
   
   //0代表灯是关着的，1代表灯是开着的 
   bool p[100] = {0}; 
   
   for ( int i = 1; i <= k; i++) {
       for (int j = 0; j < n; j++) {
           if ( (j + 1) % i == 0) {//把是第i个人倍数的灯给打开或者关上 
               p[j] = !p[j];//或者异或1 
           }
       }
   }
   
   for ( int i = 0; i < n; i++) {
       if ( p[i] == 1) {//如果是1代表是开着的，打印 
           printf("%d ", i + 1);
       }
   }
   
	return 0;
}

3. 问题C:LY不会用数组

解题思路

  1. 把输入的数的每一位都存放到数组当中
  2. 给数组用选择法从小到大排序
  3. 打印数组

解题方法

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>

int main(int argc,char *argv[])
{
   int m = 0;
   
   scanf("%d", &m);//输入m的值 
   
   int size = 100;
   int *p = (int*)malloc(sizeof(int) * size);//开辟一个数组 
   
   //把每一位的数字取出来 
	for ( int i = 0; i < size; i++)  {
		p[i] = m % 10;
		m /= 10;
	}
	
	//选择法排序 
	for (int i = 0; i < size - 1; i++) {
		int min = i;
		for ( int j = i + 1; j < size; j++) {
			if ( p[min] > p[j])	 {
				min = j;
			}
		}
		if ( min != i) {//如果要交换 
			p[min] ^= p[i];
			p[i] ^= p[min];
			p[min] ^= p[i];
		}
	}
	
	//打印结果 
	for ( int i = 0; i < size; i++)  {
		printf("%d ", p[i]);
	}
   
	return 0;
}

4. 问题D：级数求和

解题思路

  1. 观察这个数列发现它的分子都是1，分母是正整数
  2. 用循环来求和，当Sn大于k时结束循环
  3. 打印n - 1

解题方法

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>

int main(int argc, char *argv[])
{
   int k = 0;
   
   scanf("%d", &k);
   
  double sum = 0;//float精度不够 
  int i = 1;
  
    for ( i = 1; sum <= (double)k; i++ ) 
    {
       sum += 1.0 / i;
    }
   
   printf("%d", i - 1);//循环结束时i多加了1
	return 0;
}

易错点

  1. Sn的值可能会超出float的精度范围，所以在写小数点的题时要注意数据的精度是否满足要求
  2. 当循环结束时，i还会加1，所以我们输出的是i - 1的值

5. 问题E：判断升序

解题思路

  1. 如果一个数组是升序，那么它们相邻两个元素的大小必定是前面小，而后面大
  2. 如果是前面大，后面小就一定不是升序，类似冒泡的过程

解题方法

#include <stdio.h>

int main()
{
    int n = 0;
    
    scanf("%d", &n);
    
    int *p = (int*)malloc(sizeof(int) * n);
    
    for (int i = 0; i < n; i++){
        scanf("%d", p + i);
    }
    
    int i = 0;
    
    for (; i < n - 1; i++) {
        if ( p[i] > p[i + 1]) {
            break;
        }
    }
    
    if (i >= n - 1) {
        printf("YES");
    }
    else {
        printf("NO");
    }
    
    return 0;
}

6. 问题F：行排序

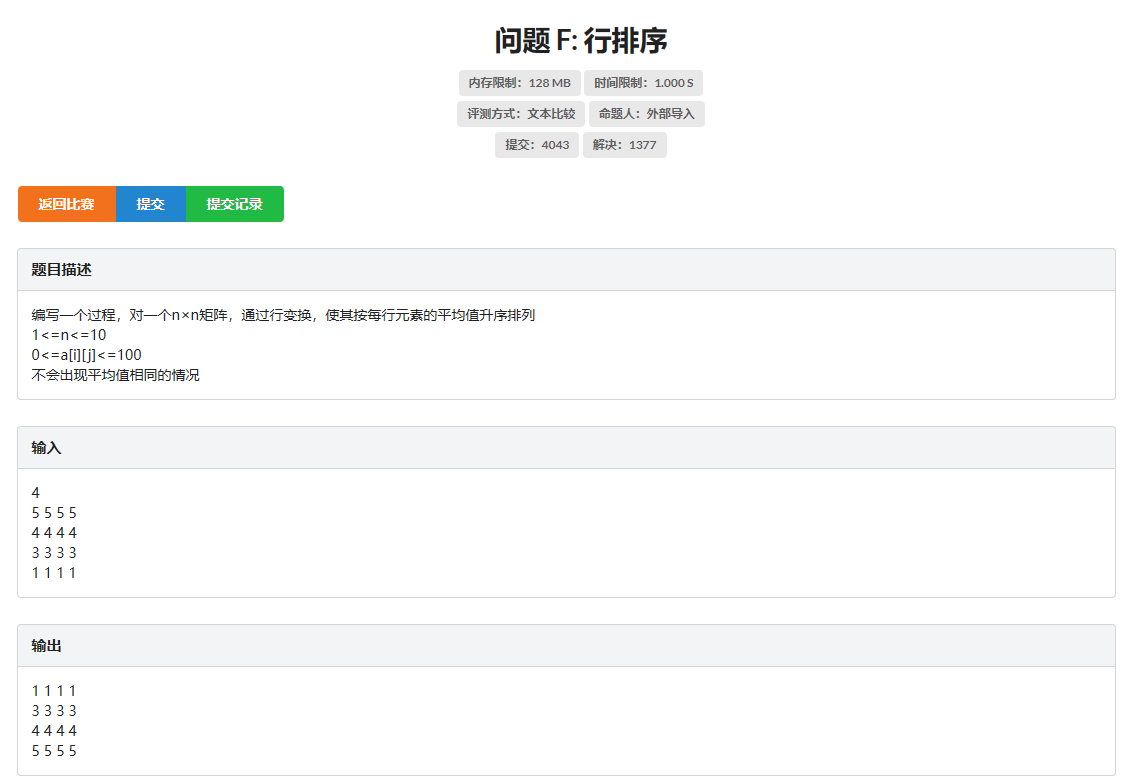
解题思路

  1. 算出各行的平均值
  2. 按各行的平均值排序
  3. 打印排序之后的数组

解题方法

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>

int main(int argc, char *argv[])
{
	int n = 0;
	
	scanf("%d", &n);
	
	int *p = (int*)malloc(sizeof(int) * n * n);//开辟一个n*n的一维数组来模拟二维数组 
	
	//赋值
	for (int i = 0; i < n; i++)
		for ( int j = 0; j < n; j++) {
			scanf("%d", p + i * n + j); 
		}
	
	float average[n];//存放各行的平均值 
	
	//计算各行的平均值 
	for (int i = 0; i < n; i++){
		float sum = 0;
		for ( int j = 0; j < n; j++) {
				sum += p[i * n + j];
		}
		average[i] = sum / n;
	}
	//用选择排序对各行的平均值进行排序		
	for ( int i = 0; i < n - 1; i++) {
		int min = i;
		for ( int j = i + 1; j < n; j++) {
			if ( average[min] > average[j]) {
			    min = j;
			}
		}
		
		if ( min != i) {
			//把最小的一行和第i行进行交换 
		    for ( int m = 0; m < n; m++) {
		        p[i * n + m] ^= p[min * n + m];
		        p[min * n + m] ^= p[i * n + m];
		        p[i * n + m] ^= p[min * n + m];
		    }
		    //最小的平均值和第i个平均值进行交换 
		    float t = 0.0;
		    t = average[i];
		    average[i] = average[min];
		    average[min] = t;
		}
	}
	
	//打印结果 
	for ( int i = 0; i < n; i++){
	    for (int j = 0; j < n; j++)
	        printf("%d ", p[i * n + j]);
	    putchar('\n');
	}
	    
	return 0;
}

7. 问题G：摘陶陶

解题思路

  1. 题目要求摘取的顺序按照输入的“苹果够到的最大高度”的顺序来摘
  2. 所以我们给苹果的高度和陶陶的高度排个序
  3. 然后给每个苹果找一个更它最接近的陶陶
  4. 只要陶陶的高度不为0，我们就可以摘，摘了之后m的值减1
  5. 当遍历完整个苹果的数组之后打印m的值

解题方法

#define  _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <time.h>
#include <stdbool.h>
#define ll long long
#define sc scanf
#define pr printf

void quickSort(int *a, int low, int high);
void swap(int *a, int low, int high);//交换a[low]和a[high]的值 
int* partition(int *a, int low, int high);//把a中low到high的数分类，小于的在左边，等于的在中间，大于的在右边

int main(int argc, char *argv[]) 
{
	int n,m;
	
	sc("%d%d", &n, &m);//输入苹果和陶陶的值
	
	int *apple = (int*)malloc(sizeof(int) * n);//开辟存放苹果高度的数组
	int *tao = (int*)malloc(sizeof(int) * m);//开辟存放陶陶高度的数组

    //输入苹果的高度
	for (int i = 0; i < n; i++)
	{
		sc("%d", apple + i);
	}

     //输入陶陶的高度
	for (int i = 0; i < m; i++)
	{
		sc("%d", tao + i);
	}

    //给苹果和陶陶的高度排序
	quickSort(tao, 0, m - 1);
	quickSort(apple, 0, n - 1);

    //给每个苹果找一个可以摘到的陶陶
	for (int i = n - 1; i >= 0; i--)
	{
		for (int j = m - 1; j >= 0; j--)
		{
			if (tao[j] != 0 && apple[i] > tao[j])//如果陶陶的高度不为0且苹果可以摘到陶陶
			{
				m--;//陶陶的数量减1
				tao[j] = 300;//设置为最大的高度，下一循环就不会摘到相同的陶陶
				break;//因为一个苹果只能摘一个陶陶所以跳出，去看下一个苹果
			}
		}
	}
	
	printf("%d", m);//打印剩下的陶陶
	
    return 0;
}
void quickSort(int *a, int low, int high)
{
	int *p = NULL;//存储等于基准值的左右边界 
	
	if ( low >= high) {//如果只有一个值不用排序就直接结束排序 
		return ;
	}
	
	swap(a, low + rand() % (high - low + 1), high);
	p = partition(a, low, high);
	quickSort(a, low, p[0] - 1);
	quickSort(a, p[1] + 1, high);
	free(p);
}
void swap(int *a, int low, int high)
{
	int t = 0;
	
	t = a[low];
	a[low] = a[high];
	a[high] = t;
}
int* partition(int *a, int low, int high)
{
	int l = low - 1;
	int r = high;
	int i = low;
	int key = a[high];
	while(i < r) {
		if (a[i] < key) {
			swap(a, l + 1, i);
			i++;
			l++;
		}
		else  if ( a[i] > key){
			swap(a, r - 1, i);
			r--;
		}
		else {
			i++;
		}
	}
	swap(a, r, high);
	int *p = (int *)malloc(sizeof(int ) * 2);
	p[0] = l + 1;
	p[1] = r;
	return p;
}

标签：11,-------,int,题解,high,++,low,include,swap
From： https://www.cnblogs.com/lwj1239/p/17810921.html

相关文章

  • Rockchip RK3399 - DRM encoder、connector基础知识
    3.1.3structdrm_connectorlinux内核使用structdrm_connector来表示一个连接器，用于连接编码器和显示设备。3.1.3structdrm_encoderlinux内核使用structdrm_encoder来表示一个编码器，用于连接CRT控制器和显示设备。3.2structdrm_devicelinux内核使用structdrm_device来......
  • 2023年11月第一周第二次总结
    1.动态规划在我看来动态规划就是用一种缓存机制来保存之前求解的答案，如果要再次用到已经求解过的答案就直接把缓存里面的答案给他而不必再次求解，也就是用空间换取时间那么要解决动态规划问题，最好按照以下步骤来求解用暴力递归来求解问题能用记忆化搜索就先用记忆化搜索......
  • 电子公文系统--确定分工
    电子公文系统三--确定分工一、规格需求说明书的修改在引言方面，我们增加了电子公文系统的使用说明；在功能方面，我们在表达方面有所欠缺，本次采用分层叙述，更加的条理清楚，在功能实现有所欠缺，部分功能没有考虑到。更改之后的规格需求说明书网址：规格需求说明书二、代码规范和编码1.代......
  • 11月3日前端需要学习的知识、自闭合标签、meta标签、div标签
    目录前端需要学习的知识生成的网页类型静态网页动态网页网页的架构c/s架构b/s架构浏览器的特别用法第一种结合python来使用第二种将文件拖入浏览器里面(这就符合渲染了)重点HTML首先!DOCTYPEhtml其次就是html到/html还有就是head到/head的内部最后就是body到/body总结其它的标签......
  • CSP-S2023总结
    CSP-S2023总结T1简单模拟，我因为对题目的理解错误丢了分，这是很不应该的。T2DP，我因为对dp不太熟练，同时对题意同样理解有误，导致暴力分只有10分。T3大模拟，我在看题之后并没有计划在这上面花太多时间，再加上T1，T2失误导致的时间紧张，我没有在这题上得分。T4算是思维题，我没有对它进行充......
  • Rockchip RK3399 - DRM HDMI驱动程序
    ----------------------------------------------------------------------------------------------------------------------------开发板：NanoPC-T4开发板eMMC：16GBLPDDR3：4GB显示屏：15.6英寸HDMI接口显示屏u-boot：2023.04linux：6.3----------------------------------......
  • CF1196B
    题意：n个数，分割成k个部分，使得每份和都为奇数做法：一个序列的和的奇偶性和偶数没关系，所以只需要考虑奇数的个数现在考虑两个问题：1.如果奇数的个数小于最终要求的k,那么就无法完成分类（即是如果一个数一块也不行）2.如果奇数的个数，记为cnt，cnt的奇偶性和k的奇偶性不同，例如cnt为3，k为2......
  • AI正在改变人类社会 - 内容行业的衰落
    现在的AI技术，每天都在进化。我有一种感觉，普通人大概没意识到，它马上就要改变人类社会了。历史上，这种事一再发生。在你不知不觉中，某些大事件悄悄酝酿，突然就冲击到了你的生活，将你的人生全部打乱，你却毫无准备。首当其冲，受到AI冲击的将是内容行业。我们以后消费的内容，绝大部分将都......
  • 资料分析-特殊考点
    一、拉动增长和增量贡献率公式例题2007年前三季度，A市完成工业总产值15777.56亿元，比去年同期增长16.2%。六个重点发展工业行业是本市工业增长的主要拉动力，前三季度共完成工业总产值10282.8亿元，比去年同期增长19.3%。2007年前三季度，六个重点发展工业行业拉动全市工......
  • 基于移动端的个人博客系统的设计与实现-计算机毕业设计源码+LW文档
    摘要博客系统是能够让网民记录分享和学习的一个网站，在博客中我们可以发表文章对感兴趣的事情进行讨论。而基于移动端的个人博客系统的设计是就为了迎合广大用户需求创建的一个界面简洁、有定向内容、业务逻辑简单易操作的博客系统。本文以博客系统的设计与实现为例，提出了利用And......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99