前言
本题解内容均摘自我的 Tarjan 学习笔记 。
解法
Tarjan 与无向图
无向图与割点(割顶)
-
在一个无向图中,不存在横叉边(因为边是双向的)。
-
一个无向图中,可能不止存在一个割点。
-
割点(割顶):在一个无向图中,若删除节点 \(x\) 以及所有与 \(x\) 相关联的边之后,图将会被分成两个或者两个以上不相连的子图,那么称 \(x\) 为这个图的割点(割顶)。
-
判定法则:
当遍历到一个节点 \(x\) 时,这个点为割点的情况有两种:- 该节点为根节点且子节点的个数大于 \(1\)(易知此时对于 \(x\) 的任意一个子节点 \(y\) 都有 \(dfn_x<low_y\)),则删掉这个节点 \(x\) 后必将导致子节点不连通,即该节点 \(x\) 为图的一个割点。
- 该节点不为根节点,且存在一个子节点 \(y\) 使得 \(dfn_x \le low_y\)(子节点 \(y\) 可回溯到的最早节点不早于 \(x\) 点,即子节点 \(y\) 无法回到 \(x\) 的祖先节点),则删掉这个节点 \(x\) 后必将导致 \(x\) 的父节点与 \(x\) 的子节点不连通,即该节点 \(x\) 为图的一个割点。
- 若不存在一个子节点 \(y\) 使得 \(dfn_x \le low_y\),说明子节点 \(y\) 能绕行其他边到达比 \(x\) 更早访问的节点,\(x\) 就不是本图的割点,即环内的点割不掉。
-
应用:如图,节点 \((0,4,5,6,7,11)\) 为割点。

无向图与双连通分量
- 若一个无向连通图不存在割点,则称它为点双连通图。
- 无向图中极大的点双连通子图叫点双连通分量,即 v-DCC。
- 在一张连通的无向图中,对于两个点 \(x\) 和 \(y\),如果删去哪个点(只能删去一个,且不能删去 \(x\) 和 \(y\) 自己)都不能使它们不连通,我们就说 \(x\) 和 \(y\) 点双连通。
点双连通分量
- 点双连通分量
-
若某个点为孤立点,则它自己单独构成一个 v-DCC。
-
除了孤立点之外,点双连通分量的大小至少为 \(2\)。
-
性质
-
点双连通分量之间以割点连接,且两个点双连通分量之间有且只有一个割点。
-
证明:若两个点双连通分量之间共用两个点,则删除其中任意一个点,所有点依旧连通。如图
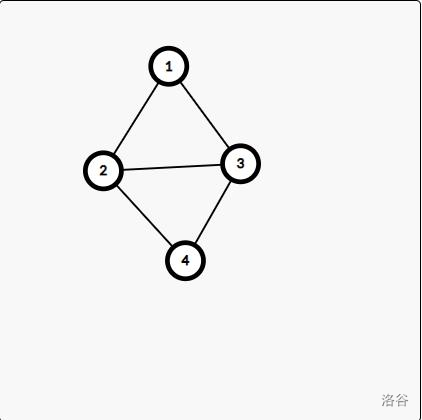
-
-
每一个割点可任意属于多个点双连通分量,因此求点双连通分量时,可能包含重复的点。
-
每一个割点都在至少两个点双连通分量中。
- 证明:在一个非点双连通图中,删去割点后图会不连通,故割点至少连接着图的两部分。但是因为点双连通图中不存在割点,所以这两部分肯定不在同一个点双连通分量中。因此割点至少存在于两个点双连通分量中。
-
只有一条边连通的两个点也是一个点双连通分量。如图
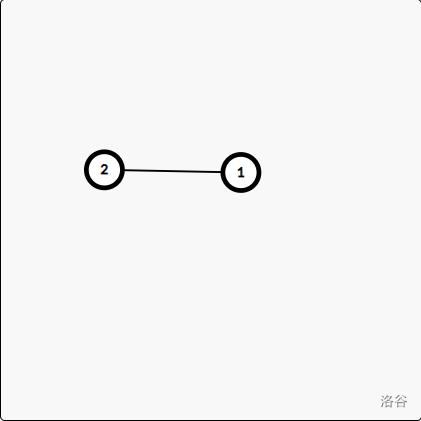
-
除了上一条中的情况外,其他的点双连通分量都满足任意两点间都存在不少于两条点不重复路径。
-
任意一个不是割点的点都只存在于一个点双连通分量中。
-
点双连通不具有传递性,如图,\((1,3)\) 点双连通,\((1,7)\) 点双连通,但是 \((3,7)\) 不点双连通。
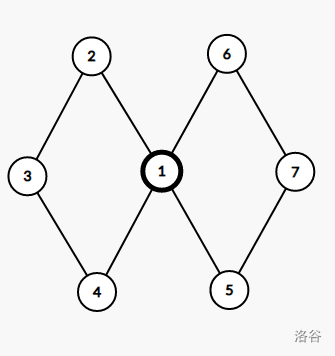
-
-
应用:如图,存在 \((1,2,3),(3,4),(4,5,6)\) 这三个点双连通分量。

-
算法
- 用一个栈存点,若遍历回到 \(x\) 时,发现割点判定法则 \(dfn_x \le low_y\) 成立,则从栈中弹出节点,直到 \(y\) 被弹出。那么,刚才弹出的节点和 \(x\) 一起构成一个 v-DCC。
-
例题
- luogu P8435 【模板】点双连通分量
- 事实上在求割点的同时,同时可以顺便求出点双连通分量,维护一个栈在求割点的途中若有 \(dfn_x>low_y\),则将 \((x,y)\) 入栈;而当 \(dfn_x \le low_y\) 时,将栈中所有在 \((x,y)\) 之上的边全部取出,这些边所连接的点与 \(x\) 构成了一个点双连通分量,显然割点是可以属于多个点双连通分量的。
- 每当新搜到一个节点时,将其压入栈中。
- 当发现 \(x\) 的子节点 \(y\) 不能通过其他方式到达 \(x\) 的祖先,但可以到达 \(x\)(即 \(dfn_x \le low_y\) 成立),则弹出栈顶元素直到 \(y\) 弹出。
- 弹出的所有元素组成的集合 \(E\) 加上 \(x\),则为一个点双连通分量。
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to; }e[4000001]; vector<int>v_dcc[4000001]; stack<int>s; int head[4000001],dfn[4000001],low[4000001],cnt=0,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x,int fa) { int i,k=0; if(x==fa&&head[x]==0)//孤立点判定 { ans++; v_dcc[ans].push_back(x); } tot++; dfn[x]=low[x]=tot; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to,fa); low[x]=min(low[x],low[e[i].to]); if(low[e[i].to]>=dfn[x]) { ans++; v_dcc[ans].push_back(x); while(e[i].to!=k)//弹栈时不能弹出割点,因为割点属于多个点双连通分量 { k=s.top(); v_dcc[ans].push_back(k); s.pop(); } } } else { low[x]=min(low[x],dfn[e[i].to]); } } } int main() { int n,m,i,j,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; if(u!=v)//重边会影响结果,记得特判 { add(u,v); add(v,u); } } for(i=1;i<=n;i++) { if(dfn[i]==0)//注意图可能不连通 { tarjan(i,i); } } cout<<ans<<endl; for(i=1;i<=ans;i++) { cout<<v_dcc[i].size()<<" "; for(j=0;j<v_dcc[i].size();j++) { cout<<v_dcc[i][j]<<" "; } cout<<endl; } return 0; }
- luogu B3610 [图论与代数结构 801] 无向图的块
- 此题中的块即为大小不为 \(1\) 的点双连通分量,故不需要判断孤立点了。
- 再按字典序排序一下就行。
#include<bits/stdc++.h> using namespace std; #define ll long long #define endl '\n' struct node { int next,to; }e[4000001]; vector<int>v_dcc[4000001]; stack<int>s; int head[4000001],dfn[4000001],low[4000001],cnt=0,tot=0,ans=0; void add(int u,int v) { cnt++; e[cnt].next=head[u]; e[cnt].to=v; head[u]=cnt; } void tarjan(int x,int fa) { int i,k=0; tot++; dfn[x]=low[x]=tot; s.push(x); for(i=head[x];i!=0;i=e[i].next) { if(dfn[e[i].to]==0) { tarjan(e[i].to,fa); low[x]=min(low[x],low[e[i].to]); if(low[e[i].to]>=dfn[x]) { ans++; v_dcc[ans].push_back(x); while(e[i].to!=k) { k=s.top(); v_dcc[ans].push_back(k); s.pop(); } } } else { low[x]=min(low[x],dfn[e[i].to]); } } } bool cmp(vector<int> x,vector<int> y) { for(int i=0;i<min(x.size(),y.size());i++) { if(x[i]!=y[i]) { return x[i]<y[i]; } } return x.size()<y.size(); } int main() { int n,m,i,j,u,v; cin>>n>>m; for(i=1;i<=m;i++) { cin>>u>>v; if(u!=v) { add(u,v); add(v,u); } } for(i=1;i<=n;i++) { if(dfn[i]==0) { tarjan(i,i); } } cout<<ans<<endl; for(i=1;i<=ans;i++) { sort(v_dcc[i].begin(),v_dcc[i].end()); } sort(v_dcc+1,v_dcc+1+ans,cmp); for(i=1;i<=ans;i++) { for(j=0;j<v_dcc[i].size();j++) { cout<<v_dcc[i][j]<<" "; } cout<<endl; } return 0; }
- luogu P8435 【模板】点双连通分量
-