CF1025F Disjoint Triangles

虽然我不懂计算几何，但是两个三角形互相进入，感觉很涩啊！ —— By 【】

考虑两个互不相交的三角形，寻找一个方式能够不重不漏地统计它们。

容易发现两条不交的线段 \(A_1A_2,B_1B_2\) 之间，必然存在一条直线将 \(A_1A_2,B_1B_2\) 分在直线两端，且与 \(A_1A_2,B_1B_2\) 无交。证明的话，随意将 \(A_1A_2\) 或者 \(B_1B_2\) 线段向对方平移一小段即可。我们发现三角形也存在这样的性质，也就是两个不交的三角形之间必然存在一条直线把它们分到直线两侧，证明同理。

事实上这样的直线有无限条，拎出任意一条这样的直线 \(l\) 进行旋转，发现最后这条直线 \(l'\) 会过两个三角形至少 \(2\) 个顶点，且这样的直线 \(l'\) 只有 \(2\) 条（一条顺时针旋转，一条逆时针旋转），如图：

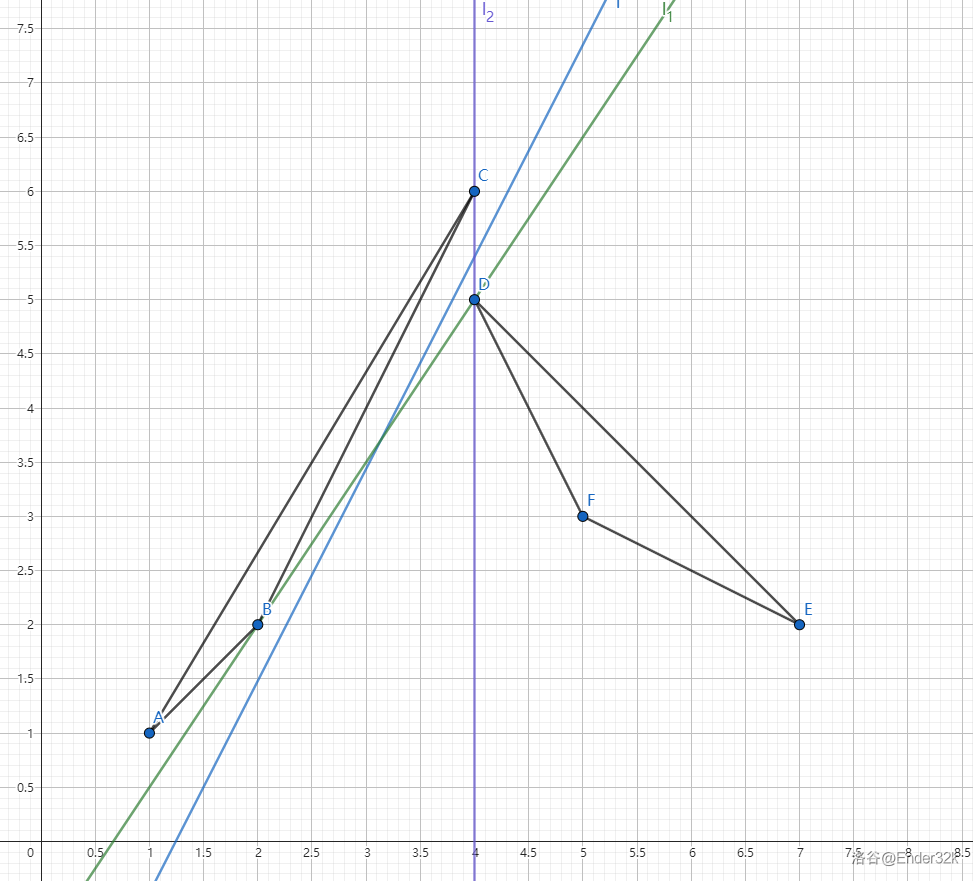
我们可以找到一条两个三角形之间的蓝色直线 \(l\)，顺时针旋转得到直线 \(l_1:BD\)，逆时针旋转得到直线 \(l_2:CD\)。

于是我们就可以枚举 \(l_1,l_2\) 了，具体地：

• 枚举直线 \(l\) 的一个端点 \(P_x\)，将 \(P_x\) 当作坐标原点，对所有向量 \(\overrightarrow{P_xP_y}(y\in \{1,2,\cdots ,x-1,x+1,\cdots ,n\})\) 进行极角排序。
• 对于一条直线 \(P_xP_y\)，考虑统计以 \(P_xP_y\) 作为 \(l_1/l_2\) 的三角形对。设在 \(P_xP_y\) 上方的点的个数为 \(c\)，那么合法的三角形对数为 \(2\dbinom{c}{2}\dbinom{n-2-c}{2}\)（乘 \(2\) 是因为同一边的两个点既可以连 \(P_x\) 也可以连 \(P_y\)）。
• 由于已经进行极角排序，所以顺序枚举所有 \(P_xP_y\)，然后双指针就可以动态维护 \(c\)，统计答案即可。

最后每个三角形对被 \(l_1\) 算了一遍，被 \(l_2\) 也算了一遍。所以答案要除以 \(2\)。

复杂度 \(O(n^2\log n)\)。

// Problem: F. Disjoint Triangles
// Contest: Codeforces - Codeforces Round 505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final)
// URL: https://codeforces.com/problemset/problem/1025/F
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
#define pb emplace_back
#define mt make_tuple
#define mp make_pair
#define fi first
#define se second

using namespace std;
typedef double db;
typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int> tu;
bool Mbe;

const int N = 2e3 + 200;
const db Pi = acos(-1);

struct vec {
	int x, y;
	vec () { }
	vec (int _x, int _y) : x(_x), y(_y) { }
	vec operator + (const vec &rh) const { return vec(x + rh.x, y + rh.y); }
	vec operator - (const vec &rh) const { return vec(x - rh.x, y - rh.y); }
	vec operator - () const { return vec(-x, -y); }
	db arc() { return atan2(y, x); }
} a[N], b[N];
int n;
db d[N];

int f(int x) { return x * (x - 1) / 2; }
ll calc(int x) {
	vector<int> dn, up;
	for (int i = 1; i <= n; i++) {
		if (i == x) continue;
		b[i] = a[i] - a[x], d[i] = b[i].arc();
		if (d[i] <= 0) dn.pb(i);
		else up.pb(i);
	}
	ll res = 0;
	sort(dn.begin(), dn.end(), [](int &x, int &y) { return d[x] < d[y]; });
	sort(up.begin(), up.end(), [](int &x, int &y) { return d[x] < d[y]; });
	for (int i = 0, j = 0, ct = up.size(); i < dn.size(); i++) {
		while (j < up.size() && d[up[j]] <= Pi + d[dn[i]]) j++, ct--;
		if (i) ct++; res += 1ll * f(ct) * f(n - 2 - ct);
	}
	return res;
}

void solve() {
	cin >> n;
	for (int i = 1, x, y; i <= n; i++)
		cin >> x >> y, a[i] = vec(x, y);
	ll res = 0;
	for (int i = 1; i <= n; i++) res += calc(i);
	cout << res << '\n';
}

bool Med;
int main() {
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cerr << (&Mbe - &Med) / 1048576.0 << " MB\n";
	#ifdef FILE
		freopen("1.in", "r", stdin);
		freopen("1.out", "w", stdout);
	#endif
	int T = 1;
	// cin >> T;
	while (T--) solve();
	cerr << (int)(1e3 * clock() / CLOCKS_PER_SEC) << " ms\n";
	return 0;
}