卡特兰数 Catalan 数列

引入

有一个无限大的栈，进栈的顺序为 \(1,2,\cdots,n\)，求有多少种不同的出栈序列。

设 \(h[n]\) 为 \(n\) 个数的出栈序列方案数。

可以这样想 \(k\) 是最后一个出栈的数，那么比 \(k\) 早进栈早出栈的有 \(k-1\) 个，方案数也就是 \(h[k-1]\)。同理比 \(k\) 晚进栈早出栈的方案数就是 \(h[n-k]\)，那么 \(k\) 作为最后一个出栈的数贡献的方案数为 \(h[k-1]h[n-k]\)。

由于 \(1\) 到 \(n\) 中任何一个数都可以成为 \(k\)，那么 \(h[n]\) 的方案数就是 \(h[n]=\sum_{i=1}^n h[i-1]h[n-i]\)。

\(h\) 就是卡特兰数列。

应用问题

• 1.有 \(2n\) 个人排队买票，票 \(5\) 元一张。有 \(n\) 个人有 \(5\) 元钞票，另外 \(n\) 个人有 \(10\) 元钞票，售票处没有其它钞票，求有多少种排队顺序不会使售票处无法找零。

  分析：每一个 \(10\) 元的钞票都需要一个 \(5\) 元的钞票，不妨把 \(5\) 元看成进栈 \(10\) 元看成出栈，每一种出栈序列对应一种排队方案，问题变为引入问题，答案为 \(h[n]\)。

• 2.学校在坐标 \((n,n)\) 处，每天彬彬上学会从 \((0,0)\) 出发，向 \(x\) 轴正方向走 \(n\) 步，向 \(y\) 轴正方向走 \(n\) 步，求不穿过（可以碰到）\((n,n)\) 与 \((0,0)\) 对角线（即直线 \(y=x\)）的路径数（只走直线 \(y=x\) 下方）。

  分析：如果想不穿过对角线那么可以移动看做进栈和出栈。如上题，一种出栈序列对应一种路径方案，答案为 \(h[n]\)。

总结：对于一些问题，可以转换成不同出栈序列的问题，那么便可以由卡特兰数得到。

• 3.有一个 \(n\) 条边的凸多边形，用直线连接对角线，使该多边形分为多个三角形，每条直线不相交，问有多少种划分方法。

  分析：我们先将多边形顺序编号 \(p_1,p_2,\cdots,p_n\)，选择基边 \(p_1p_n\)，再任选一个点 \(p_k\ (2\leq k \leq n-1)\)，连接 \(p_1p_k,p_np_k\)，这样（除连接的三角形外）将多边形重新分为了一个 \(k\) 边型和 \(n-k+1\) 边型，那么设 \(f[n]\) 为 \(n\) 边型的答案，有 \(f[n]=\sum_{i=1}^n h[i-1]h[n-i]\)。这正是卡特兰数的递推公式。

• 4.圆环上有 \(2n\) 个点，求点成对连接，线段不相交的方案数。

  分析：和上述一样，选择后点对后会分为两部分，将两部分独立处理即可。

总结：如果一个问题可以通过枚举来分为两部分，通过乘法和加法原理得到相同的递推式，那么也是卡特兰数列。在做题中，我们可以先设 \(dp\) 在推式子，得出 \(dp\) 的递推公式，再来判断卡特兰数；或者先看能否分为两部分，再推式子。

公式

使用应用问题 \(2\) 推导：

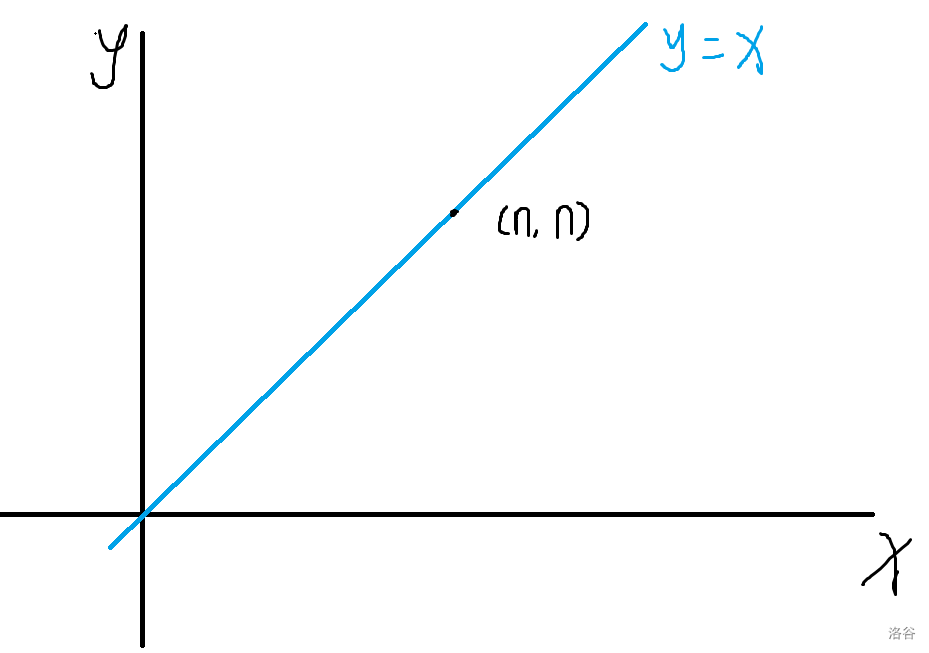
先不管不管对角线限制，从 \((0,0)\) 到 \((n,n)\) 的路径数为 \(C_{2n}^n\)。

在减去穿过对角的路径数，即减去触碰到 \(y=x+1\) 的直线的路径数。

把一条路径碰到 \(y=x+1\) 之前的路径以 \(y=x+1\) 为对称轴翻转，发现每次的起点都变成 \((-1,1)\)。

图中黄线为原触碰 \(y=x+1\) 的路径，灰色为关于 \(y=x+1\) 翻折的部分。

那么不合法线段的选择数就是从 \((-1,1)\) 走到 \((n,n)\) 的方案数。（无论怎么走都会触碰红线）

那么合法的方案数就是 \(总方案数-不合法方案数\)，即 \(h[n]=C_{2n}^n-c_{2n}^{n-1}\)。

化简后变得到了 \(h[n]\) 的递推式，\(h[n]=C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}\)。