标签：attraction 512D 题解样例 int Fox she 根树 Travelling

Fox And Travelling

题面翻译

给定一张 $n$ 个点 $m$ 条边的无向图。
一个点只有当与它直接相连的点中最多只有一个点未被选择过时才可被选择。
询问对于每个 $k \in [0,n]$，有序选择 $k$ 个点的方案数。
$n \le 100$，$m \le \frac{n(n-1)}2$，答案对 $10^9+9$ 取模。

题目描述

Fox Ciel is going to travel to New Foxland during this summer.

New Foxland has $ n $ attractions that are linked by $ m $ undirected roads. Two attractions are called adjacent if they are linked by a road. Fox Ciel has $ k $ days to visit this city and each day she will visit exactly one attraction.

There is one important rule in New Foxland: you can't visit an attraction if it has more than one adjacent attraction that you haven't visited yet.

At the beginning Fox Ciel haven't visited any attraction. During her travelling she may move aribtrarly between attraction. After visiting attraction $ a $ , she may travel to any attraction $ b $ satisfying conditions above that hasn't been visited yet, even if it is not reachable from $ a $ by using the roads (Ciel uses boat for travelling between attractions, so it is possible).

She wants to know how many different travelling plans she can make. Calculate this number modulo $ 10^{9}+9 $ for every $ k $ from $ 0 $ to $ n $ since she hasn't decided for how many days she is visiting New Foxland.

输入格式

First line contains two integers: $ n $ , $ m $ ( $ 1<=n<=100 $ , 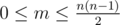), the number of attractions and number of undirected roads.

Then next $ m $ lines each contain two integers $ a_{i} $ and $ b_{i} $ ( $ 1<=a_{i},b_{i}<=n $ and $ a_{i}≠b_{i} $ ), describing a road. There is no more than one road connecting each pair of attractions.

输出格式

Output $ n+1 $ integer: the number of possible travelling plans modulo $ 10^{9}+9 $ for all $ k $ from $ 0 $ to $ n $ .

样例 #1

样例输入 #1

3 2
1 2
2 3

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

样例 #4

样例输入 #4

13 0

样例输出 #4

提示

In the first sample test for $ k=3 $ there are 4 travelling plans: $ {1,2,3},{1,3,2},{3,1,2},{3,2,1} $ .

In the second sample test Ciel can't visit any attraction in the first day, so for $ k>0 $ the answer is $ 0 $ .

In the third sample test Foxlands look like this:

题目

给定一张 n 个点 m 条边的无向图。一个点只有当与它直接相连的点中最多只有一个点未被遍历过时才可被遍历。询问对于每个 k ∈ [0, n]，遍历 k 个点的方案数。约束条件如下：

n ≤ 100
m ≤ (n-1)^2
答案对 10^9 + 9 取模

题解

首先，在环中的点一定不会被遍历。

用类似拓扑排序的过程可以把环上的点全部扔掉，剩下的点会构成若干个有根树和无根树，其中有根树的根是树中唯一与环中的点相连的点。

每棵树求出答案后，01 背包合并即可，中间只需要乘上一个组合数。

对于有根树，设 fi,j 为 i 的子树中选 j 个的方案数，那么就是树上背包，同样需要乘上一个组合数。

对于无根树，以树中每个点为根做一次有根树的树上背包，这样会发现每种选择 i 个点的方案会被多算 s-i 次，其中 s 为这棵无根树的大小，那么除掉即可。

总时间复杂度 O(n^3)，其中背包经过了上下界优化，原理简单来说就是「每对点只会在 LCA 处合并一次」。

、

const int N = 107;
int n, m, d[N], w[N], b[N], s[N], S;
vi e[N];
modint p[N], v[N], vp[N], f[N][N], ans[N];

inline modint C(int a, int b) {
    return p[a] * vp[b] * vp[a-b];
}

void dfs(int x, int o, int &s) {
    b[x] = o, ++s;
    for (ui i = 0; i < e[x].size(); i++) {
        int y = e[x][i];
        if (!d[y] && !b[y]) dfs(y, o, s);
    }
}

void dp(int x, int fa) {
    s[x] = 1, f[x][0] = 1;
    for (ui i = 0; i < e[x].size(); i++) {
        int y = e[x][i];
        if (b[x] != b[y] || y == fa) continue;
        dp(y, x);
        for (int j = 0; j < s[y]; j++) f[x][s[x]+j] = 0;
        for (int j = s[x] - 1; ~j; j--)
            for (int k = 1; k <= s[y]; k++)
                f[x][j+k] += f[x][j] * f[y][k] * C(j + k, j);
        s[x] += s[y];
    }
    f[x][s[x]] = f[x][s[x]-1];
}

void get(int x) {
    dp(x, 0);
    for (int i = 0; i <= s[x]; i++) f[0][i] += f[x][i];
}

int main() {
    rd(n), rd(m);
    p[0] = v[0] = 1;
    for (int i = 1; i <= n; i++) p[i] = p[i-1] * i;
    vp[n] = p[n] ^ -1;
    for (int i = n; i; i--) v[i] = p[i-1] * vp[i], vp[i-1] = vp[i] * i;
    for (int i = 1, x, y; i <= m; i++) rd(x), rd(y), e[x].pb(y), e[y].pb(x), ++d[x], ++d[y];
    queue<int> q;
    for (int i = 1; i <= n; i++) if (d[i] <= 1) w[i] = 1, q.push(i);
    while (q.size()) {
        int x = q.front();
        q.pop();
        for (ui i = 0; i < e[x].size(); i++) {
            int y = e[x][i];
            if (--d[y] <= 1 && !w[y]) w[y] = 1, q.push(y);
        }
    }
    for (int i = 1; i <= n; i++) if (d[i] == 1) dfs(i, i, s[i]);
    for (int i = 1; i <= n; i++) if (!d[i] && !b[i]) dfs(i, i, s[i]);
    ans[0] = 1;
    for (int i = 1; i <= n; i++)
        if (i == b[i]) {
            int o = s[i];
            if (d[i] == 1) get(i);
            else {
                for (int j = 1; j <= n; j++)
                    if (b[j] == i) get(j);
                for (int j = 0; j <= o; j++) f[0][j] *= v[o-j];
            }
            for (int j = S; ~j; j--)
                for (int k = 1; k <= o; k++)
                    ans[j+k] += ans[j] * f[0][k] * C(j + k, j);
            for (int j = 0; j <= o; j++) f[0][j] = 0;
            S += o;
        }
    for (int i = 0; i <= n; i++) print(ans[i]);
    return 0;
}

思路：https://www.luogu.com.cn/blog/xht37/solution-cf512d

标签：attraction,512D,题解,样例,int,Fox,she,根树,Travelling
From： https://www.cnblogs.com/Serein-KarBlog/p/17762884.html

Codeforces 512D. Fox And Travelling 题解