1.介绍:
manacher算法用于求解回文子串问题,可以求出以一个串中每一点为中心的最长回文半径,相当于可以求出所有回文子串
2.引入:
假如要求出一个串所有长度为奇数的回文子串,暴力怎么做?
枚举以每个点为回文中心,向两侧扩展,分别比较a[p+i]与a[p-i]
时间复杂度 O(n^2)
我们考虑优化,我们可以利用已经求解出的回文子串的信息
- 举例:a a b c b a b c
考虑回文中心在i之前的、最右端最远的一个回文子串
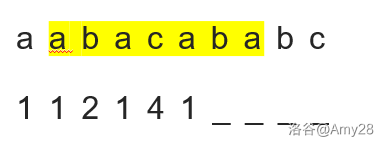
可以看出,在求解第7位b的回文半径时,我们是可以利用到第3位b的数据的
- 当然,有的时候需要注意一下

此时就要注意,不能直接利用3,而是要与最远的那个回文子串进行一个比较
因此,我们只需要记下来当前右端最远的回文子串,就可以先利用之前的信息跳过一部分试验
当然,在利用过后,还需要继续用暴力的方法拓展
对了,现在只求出了所有长度为奇数的回文子串,那么长度为偶数的怎么办?
在每两个字符之间插入特殊字符即可
例如aabbaa -> #a#a#b#b#a#a#
Code
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
#define maxn 11000010
int cnt;
int len;
char s[maxn],s_[maxn*2];
int f[maxn*2];
void make()
{
cnt=2;
s_[0]='^';
s_[1]='$';
for(int i=0;i<len;i++)
{
s_[cnt++]=s[i];
s_[cnt++]='$';
}
s[cnt]='&';
}//世界第一甜
void Manacher()
{
int mid=0,ans=0,ma=0;
for(int i=1;i<=(len*2+1);i++)
{
if(ma>i)
{
f[i]=min(ma-i,f[mid*2-i]);
}
else
{
f[i]=1;
}
while(s_[i-f[i]]==s_[i+f[i]])
{
f[i]++;
}
if(ma<(i+f[i]))
{
ma=i+f[i];
mid=i;
}
ans=max(ans,f[i]);
}
printf("%d\n",ans-1);
return;
}//华锐李泽言
int main()
{
scanf("%s",s);
len=strlen(s);
make();
Manacher();
return 0;
}