关于算法
折半搜索,又称 meet in the middle 算法。
顾名思义,就是将整个搜索的过程分成两个部分分别进行搜索,然后再将两个部分搜索出来的答案进行合并,得到最终的答案。
dfs 搜索算法一般都是指数级别的,那么我们假如每次 dfs 时都有两种决策,那么我们执行 dfs 算法的时间复杂度为 \(O(2^n)\),如果 \(n\) 再稍微大一点时,就会导致超时,那么这个时候我们就会采取折半搜索。
我们来看一下下面两张图。
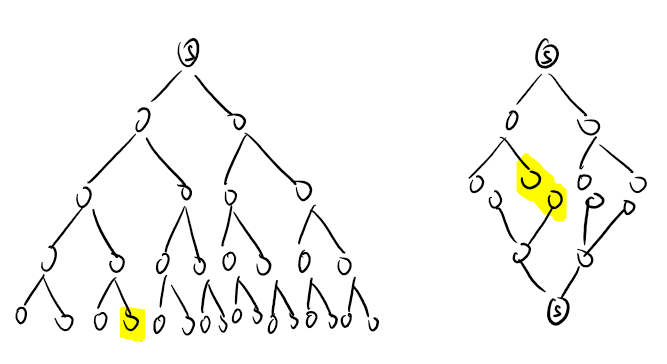
很容易发现,左边这一张图是普通的只执行 \(1\) 次的搜索树,而右边这张图则是从两个不同的点分别出发搜索产生的搜索树。
显然,左边这一个搜索树随着层数的增加,每一层的节点数成指数级增长,最终会在最后一层的某一个节点上产生答案。(假设黄色部分表示最终答案。)
而右边的折半搜索产生的搜索树,恰巧就可以避免随着层数的不断增加导致节点数大规模增长,当第二次搜索完毕之后,和第一次搜索出来的结果进行合并操作,得到最终的答案。
那么这个时候我们的折半搜索的时间复杂度就会优化为 \(O(2^{n/2})\),再加上我们合并答案的复杂度。可见相比普通的 dfs 搜索,折半搜索起到了很大的优化作用。
例题
这道题乍一看可以用背包做,但 \(1 \leq M \leq 10^{18}\),\(dp\) 数组开不了这么打,显然只能用搜索来解决。
但, \(1 \leq N \leq 40\),对于普通搜索来讲 \(O(2^n)\) 的时间复杂度还是跑不了这么大的数据,那么我们考虑折半搜索。
以 \(N \div 2\) 为界限,先搜索前面一半,并且把前面一半的数据打表储存下来(这里储存的不是方案数,而是每种方案所花的钱,原因看下面合并),再搜索后面一半,搜索完毕后与前一半合并,记得得到最终答案。
对于折半搜索来讲,难点一般都在如何合并上,对于这一道题,显然,当我们后一半搜索完毕后,我们可以对前一半的所有结果(前一半每种方案所花的钱)进行从小到大排序,再二分查找,我们看前一半中的方案所花的钱,加上当前花的钱,超不超过 \(M\),若不超过,则当钱花的钱可以和前一半所有合法的数,组成一种方案。
代码实现:
#include <bits/stdc++.h>
#define int long long
const int N = 105;
using namespace std;
inline int read(){
int r = 0,w = 1;
char c = getchar();
while (c < '0' || c > '9'){
if (c == '-'){
w = -1;
}
c = getchar();
}
while (c >= '0' && c <= '9'){
r = (r << 3) + (r << 1) + (c ^ 48);
c = getchar();
}
return r * w;
}
int n,m,arr[N],half,cnt = 0,v[1 << 24];
int ans = 0;
void dfs1(int pos,int s){
if (pos == half + 1){
cnt++;
v[cnt] = s;
return;
}
if (1ll * s + 1ll * arr[pos] <= m){
dfs1(pos + 1,1ll * s + 1ll * arr[pos]);
}
dfs1(pos + 1,s);
}
void dfs2(int pos,int s){
if (pos == n + 1){ // 合并。
ans += upper_bound(v + 1,v + cnt + 1,m - s) - v - 1; // 二分查找。
return;
}
if (1ll * s + 1ll * arr[pos] <= m){
dfs2(pos + 1,1ll * s + 1ll * arr[pos]);
}
dfs2(pos + 1,s);
}
signed main(){
n = read(),m = read();
for (int i = 1;i <= n;i++){
arr[i] = read();
}
half = n >> 1;
dfs1(1,0);
sort(v + 1,v + cnt + 1);
dfs2(half + 1,0);
printf("%lld",ans);
return 0;
}
更多练习:
CF1006F Xor-Paths
CF888E Maximum Subsequence
AcWing 171.送礼物