P3373 【模板】线段树 2

【模板】线段树 2

如题，已知一个数列，你需要进行下面三种操作：

• 将某区间每一个数乘上 \(x\)；
• 将某区间每一个数加上 \(x\)；
• 求出某区间每一个数的和。

输入格式

第一行包含三个整数 \(n,q,m\)，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 \(n\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。

接下来 \(q\) 行每行包含若干个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数乘上 \(k\)

操作 \(2\)： 格式：2 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)

操作 \(3\)： 格式：3 x y 含义：输出区间 \([x,y]\) 内每个数的和对 \(m\) 取模所得的结果

输出格式

输出包含若干行整数，即为所有操作 \(3\) 的结果。

样例输入 #1

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

样例输出 #1

17
2

提示

【数据范围】

对于 \(30\%\) 的数据：\(n \le 8\)，\(q \le 10\)。
对于 \(70\%\) 的数据：$n \le 10^3 \(，\)q \le 10^4$。
对于 \(100\%\) 的数据：\(1 \le n \le 10^5\)，\(1 \le q \le 10^5\)。

除样例外，\(m = 571373\)。

（数据已经过加强 ^_）

样例说明：

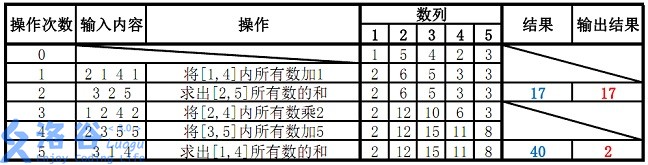
故输出应为 \(17\)、\(2\)（\(40 \bmod 38 = 2\)）。

解题思路

那么这道题有些颠覆了我对懒标记的认识，首先加和乘混在一起肯定要注意次序，那我们就以先加再乘为例，原\(a_1,a_2,a_3,\dots,a_n\)
​
变为\(a_1+t,a_2+t,a_3+t,\dots,a_n+t\)，乘上\(x\)后变为\(a_1x+tx,a_2x+tx,a_3x+tx,\dots,a_nx+tx\),那可以发现这是一个乘法分配律的过程，那么对于加的懒标记不仅要加上\(t\)，而且要乘\(x\),而对于乘的懒标记则要乘上\(x\)，所以说

#include <bits/stdc++.h>

using namespace std;
const int N = 1000010;

int a[N]; // 原数组
int n, m, p;

// 线段树模板
#define int long long
#define ls u << 1
#define rs u << 1 | 1
#define mid ((l + r) >> 1)

struct Node {
    int l, r;
    int sum;
    int mu, add;
} tr[N];

void pushup(int u) {
    tr[u].sum = (tr[ls].sum + tr[rs].sum) % p;
}

void build(int u, int l, int r) {
    tr[u].l = l, tr[u].r = r, tr[u].mu = 1;

    if (l == r) {
        tr[u].sum = a[l];
        return;
    }
    build(ls, l, mid), build(rs, mid + 1, r);
    pushup(u);
}

void pushdown(int u) {
    if (tr[u].add == 0 && tr[u].mu == 1) return; // 默认懒标记

    int &mu = tr[u].mu, &add = tr[u].add; // 此时的add懒标记，已经处理过了

    tr[ls].sum = (mu * tr[ls].sum % p + (tr[ls].r - tr[ls].l + 1) * add % p) % p;
    tr[rs].sum = (mu * tr[rs].sum % p + (tr[rs].r - tr[rs].l + 1) * add % p) % p;

    tr[ls].mu = tr[ls].mu * mu % p;
    tr[rs].mu = tr[rs].mu * mu % p;

    tr[ls].add = (tr[ls].add * mu % p + add) % p;
    tr[rs].add = (tr[rs].add * mu % p + add) % p;

    mu = 1, add = 0; // 清空懒标记
}

void add(int u, int L, int R, int v) {
    int l = tr[u].l, r = tr[u].r;
    if (l >= L && r <= R) {
        tr[u].add = (tr[u].add + v) % p;
        tr[u].sum = (tr[u].sum + v * (tr[u].r - tr[u].l + 1) % p) % p;
        return;
    }
    if (l > R || r < L) return;
    pushdown(u);
    add(ls, L, R, v), add(rs, L, R, v);
    pushup(u);
}

void mu(int u, int L, int R, int v) {
    int l = tr[u].l, r = tr[u].r;
    if (l >= L && r <= R) {
        tr[u].add = tr[u].add * v % p; // 比较重要的一步,add要在这里乘上v,因为后面可能要加其他的数而那些数其实是不用乘k的
        tr[u].mu = tr[u].mu * v % p;
        tr[u].sum = tr[u].sum * v % p;
        return;
    }
    if (l > R || r < L) return;
    pushdown(u);
    mu(ls, L, R, v), mu(rs, L, R, v);
    pushup(u);
}

int query(int u, int L, int R) {
    int l = tr[u].l, r = tr[u].r;
    if (l >= L && r <= R) return tr[u].sum;
    if (l > R || r < L) return 0;
    pushdown(u);
    return (query(ls, L, R) + query(rs, L, R)) % p;
}

signed main() {
// 文件输入输出
#ifndef ONLINE_JUDGE
    freopen("P3373.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m >> p;
    for (int i = 1; i <= n; i++) cin >> a[i];

    build(1, 1, n);

    while (m--) {
        int op, l, r;
        cin >> op >> l >> r;
        if (op == 1) {
            int k;
            cin >> k;
            mu(1, l, r, k);
        } else if (op == 2) {
            int k;
            cin >> k;
            add(1, l, r, k);
        } else
            printf("%lld\n", query(1, l, r));
    }
    return 0;
}