首页 > 其他分享 >回溯（backstracking）

回溯（backstracking）

时间：2023-08-29 12:45:35浏览次数：30  
标签：arr return int list backstracking 回溯 new backtracking

回溯（抽象成树型结构、一般无返回值backtracking）

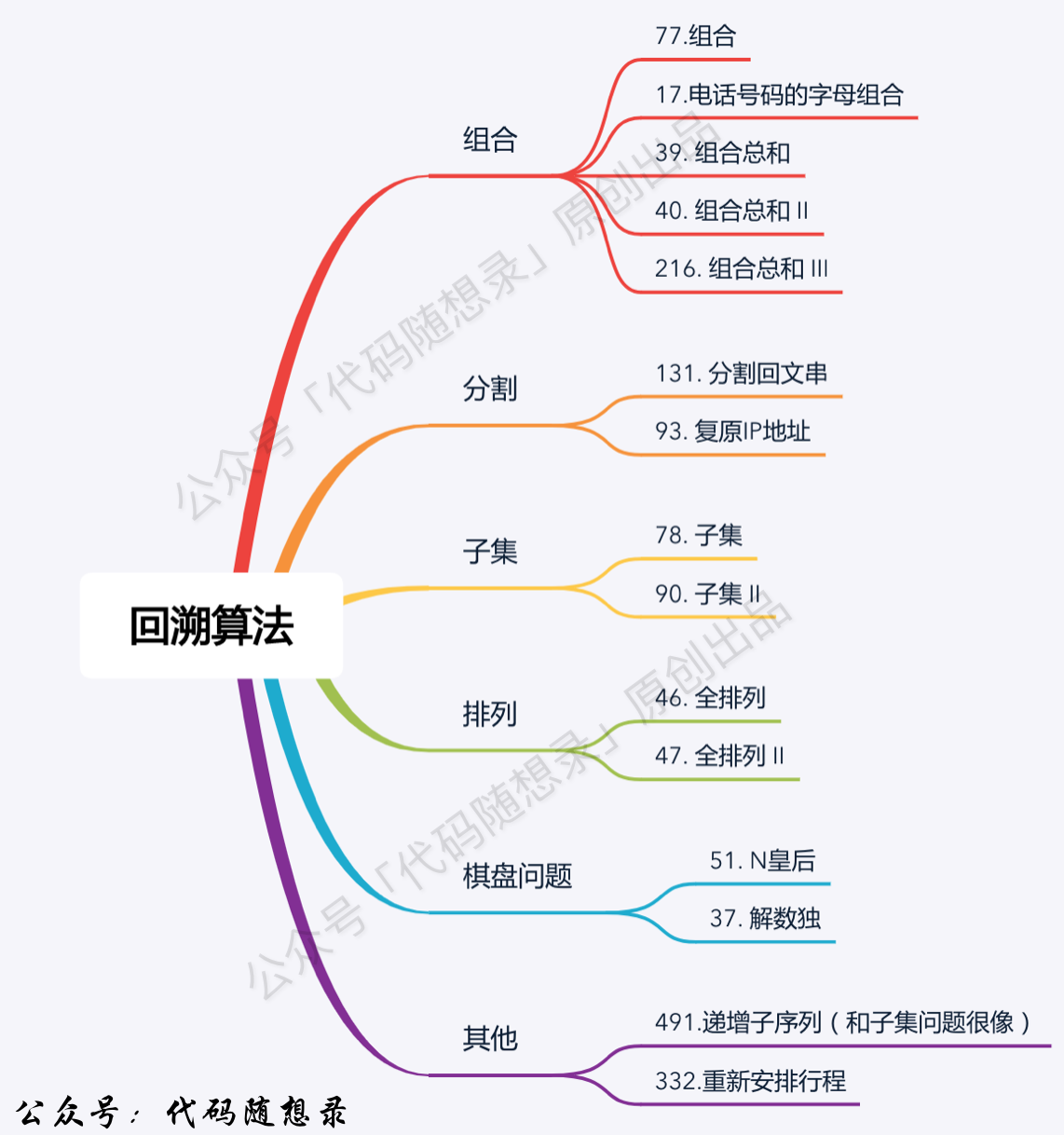
回溯算法大纲

1. 理论基础

回溯 和递归相辅相成

  • 一般递归函数下面的部分就是回溯的逻辑
  • 默认是纯暴力（后续可以剪枝）

应用：

  • 组合【没有顺序】
  • 切割
  • 子集
  • 排列【有顺序】
  • 棋盘
    • N 皇后
    • 解数独

回溯法都可以抽象为一个树型结构

  • 树的宽度：集合大小
  • 树的深度：递归深度

回溯模板

void backtracking(参数){
	if(终止条件){
		收集结果	# 通常在叶子节点
		return;
	}
	for(集合元素集){
		处理节点;
		backracking(路径、选择列表);	# 递归
		回溯，撤销处理结果
	}
}

回溯三部曲：

  1. 递归函数参数、返回值
  2. 确定终止条件
  3. 单层递归逻辑

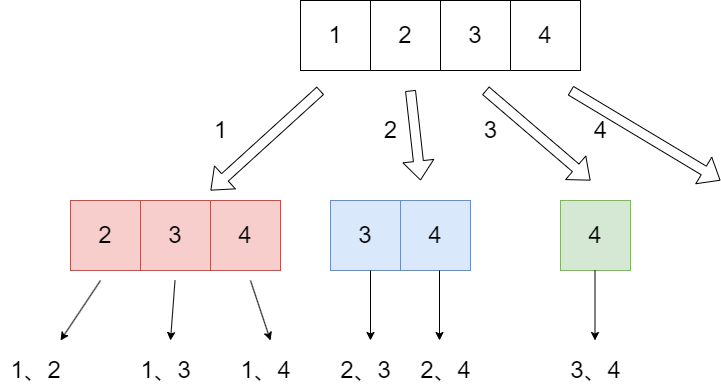
77. 组合（没有顺序）

注意：这里 k：递归的层数

ccdd

class Solution {
	List<Integer> temp =  new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
		backtracking(1, n, k);
		return res;
    }

    public void backtracking(int start, int n, int k){
    	if (k == 0){	//	到叶子节点了
    		res.add(new ArrayList<>(temp));
			return;
		}
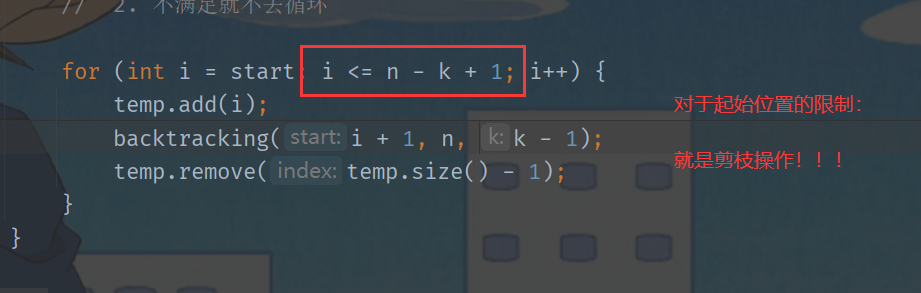
		//	注意：如果是取出第一个节点的话：i 的极限是：n - k + 1
        //	随着 temp 增大，i 的极限也会向右推进
        
		for (int i = start; i <= n - k + 1; i++) {	// i：1 -> 3【n - k + 1】
			temp.add(i);
			backtracking(i + 1, n, k - 1);
			temp.remove(temp.size() - 1);	//	回溯
		}
	}
}

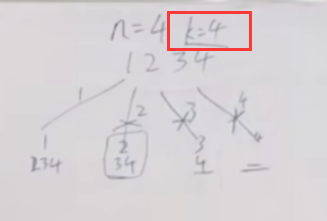
组合问题剪枝

如果早就直到达不成要求的话，就提前终止

image-20230825115653144

image-20230825123405401

216. 组合总和Ⅲ【在一个集合中求解（利用 start 避免得到重复的组合）】

注意：⭐

我们每次都要存储list 内的临时值

否则，最后

  • 由于 list 最后一定是 null
  • 而 list 是引用类型
  • 所以res 中存放的也只是 null

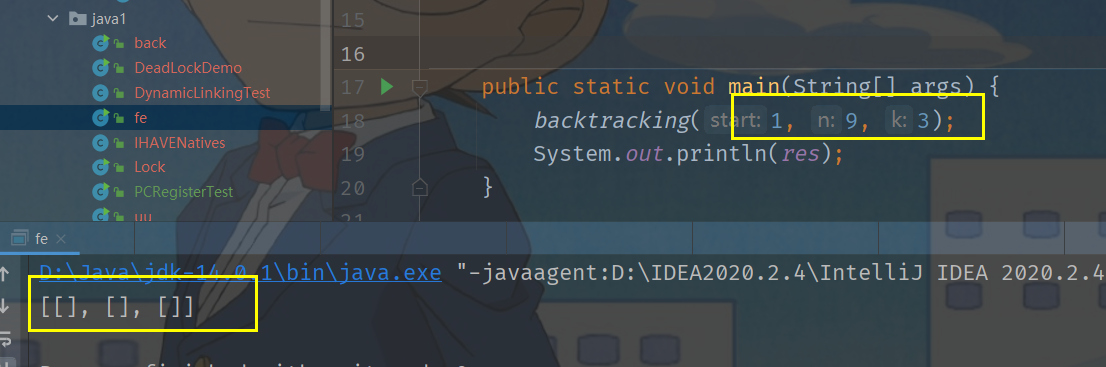
验证下：

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

# 如果猜的没错的话，res 中有三个 null

image-20230825160207794

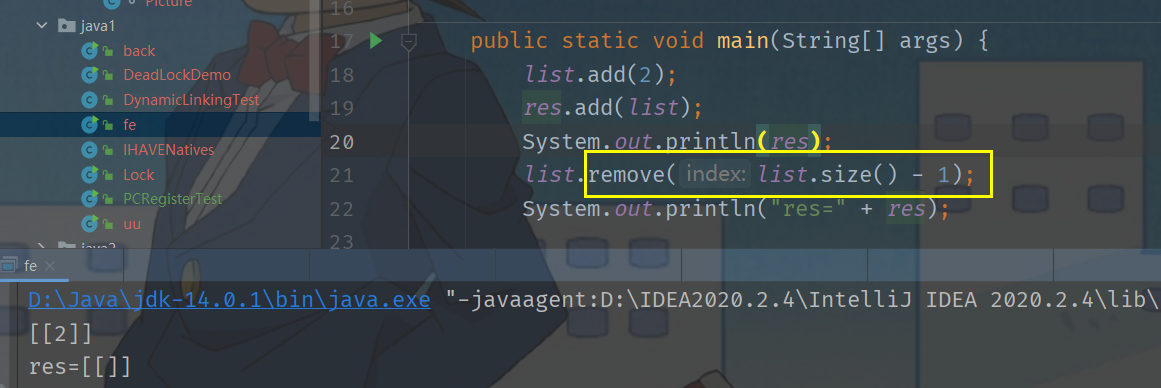
// 理解：不能直接写 res.add(list)
//	1. list 是引用类型
//	2. 由于对于list 的操作，每次都在添加后，马上清除
//	   所以如果仅仅存放 list的话只有 null
res.add(new ArrayList<>(list));

再次验证：

image-20230825160621976

class Solution {
	List<List<Integer>> res = new ArrayList<>();
	List<Integer> list = new ArrayList<>();
	//	相加和为n 的 k 个数
	public List<List<Integer>> combinationSum3(int k, int n) {
		int sum = 0;
		for (int i = 1; i <= 9; i++) {
			sum += i;
		}
		if (n > sum){
			return res;
		}
		backtracking(1, n, k);
		return res;
	}
	public void backtracking(int start, int n, int k){
		if (n == 0 && k == 0){
			res.add((new ArrayList<>(list)));
			return;
		}
		if (k == 0){
			return;
		}

		//	如果当前值 > n
		for (int i = start; i <= 9 - k + 1; i++) {	//	确定起始位置
			list.add(i);
			backtracking(i + 1, n - i, k - 1);
			list.remove(list.size() - 1);
		}
	}
}

17. 电话号码的字母组合【2个集合，无需 start】

class Solution {
	List<String> list = new ArrayList<>();
	Map<Integer, String> map = new HashMap<>();
	StringBuilder sb = new StringBuilder();
	public List<String> letterCombinations(String digits) {
		if (digits.length() == 0){
			return list;
		}
		map.put(2, "abc");
		map.put(3, "def");
		map.put(4, "ghi");
		map.put(5, "jkl");
		map.put(6, "mno");
		map.put(7, "pqrs");
		map.put(8, "tuv");
		map.put(9, "wxyz");
		backtracking(digits, 0);
		return list;
	}

	public void backtracking(String str, int index){
		if (index == str.length()){	//	指向末尾才真正结束
			list.add(sb.toString());
			return;
		}

		int temp = Integer.parseInt(str.charAt(index)+"");
		String s = map.get(temp);	//	第一个数字对应的字符串
		for (int j = 0; j < s.length(); j++) {
			sb.append(s.charAt(j));
			backtracking(str, index + 1);
			sb.delete(sb.length() - 1, sb.length());
		}
	}
}

39. 组合总和

可以重复选取

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
		backtrack(candidates, 0, target);
		return res;
	}

    public void backtrack(int[] arr, int start, int target){
    	if (target < 0){
    		return;
		}

    	if (target == 0){
			res.add(new ArrayList<>(list));
    		return;
		}
		for (int i = start; i < arr.length; i++) {
			list.add(arr[i]);
			backtrack(arr, i,target - arr[i]);	//	由于元素可以重复取，所以 这里 i 不加一了就
			list.remove(list.size() - 1);
		}
	}
}

40. 组合总和Ⅱ【组合去重，先排序，如果和上一个相同就右移】

如果用 Set 的话，底层是红黑树，效率较低！！！

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    	Arrays.sort(candidates);
		backtracking(candidates, 0, target);
		return res;
	}

	public void backtracking(int[] arr, int start, int target){
    	if (target < 0){
    		return;
		}
    	if (target == 0){
    		res.add(new ArrayList<>(list));
			return;
		}

		for (int i = start; i < arr.length; i++) {
			list.add(arr[i]);
			backtracking(arr, i + 1, target - arr[i]);
			list.remove(list.size() - 1);
			while (i < arr.length - 1 && arr[i + 1] == arr[i]){	//	如果下一步和当初选择的一致，那么跳过即可！！！
				i++;
			}
		}
	}
}

131. 分割回文串

对应的树型结构【和组合类似】

class Solution {
	List<String> list = new ArrayList<>();
	List<List<String>> res = new ArrayList<>();

    public List<List<String>> partition(String s) {
		backtracking(s, 0);
		return res;
	}

	public void backtracking(String str, int index){
    	if (index == str.length()){
    		res.add(new ArrayList<>(list));
    		return;
		}
		for (int i = index; i < str.length(); i++) {	//	注意 index 是定制
			String substring = str.substring(index, i + 1);
			if (isReverse(substring)) {
				list.add(str.substring(index, i + 1));
			}else{
				continue;
			}
			backtracking(str, i + 1);	//	在 str 的 i + 1 位置处继续递归
			list.remove(list.size() - 1);
		}
	}

	public boolean isReverse(String str){
    	int l = 0;
    	int r = str.length() - 1;
    	while (l < r){
    		if (str.charAt(l) != str.charAt(r)){
    			return false;
			}
    		l++;
    		r--;
		}
		return true;
	}
}

93. 复原 IP 地址

class Solution {
	StringBuilder sb = new StringBuilder();
	List<String> list = new ArrayList<>();
    public List<String> restoreIpAddresses(String s) {
		backtracking(s, 0, 4);
		System.out.println(list);
		return list;
	}

    public void backtracking(String str, int startIndex, int k){
    	if (startIndex == str.length() && k == 0){
    		list.add(sb.substring(0, sb.length() - 1));	//	取出末尾 .
    		return;
		}

		for (int i = startIndex; i < str.length(); i++) {
			String substring = str.substring(startIndex, i + 1);
			int len = substring.length();	//	添加字符串的长度
			if (isValid(substring)){
				sb.append(substring).append(".");
			}else {
				continue;
			}
			backtracking(str, i + 1, k - 1);
			sb.delete(sb.length() - len - 1, sb.length());
		}
	}

	public boolean isValid(String str){
		char[] chars = str.toCharArray();
		for (char aChar : chars) {
			if (!Character.isDigit(aChar)){
				return false;
			}
		}

		if (str.length() > 3) {
			return false;
		}
		int i = Integer.parseInt(str);
    	if (i < 0 || i > 255){
    		return false;
		}
		return (i + "").equals(str);	//	不含前导 0
	}
}

78. 子集【收集全部结果】

注意：这里不能提前 return

因为第一次 list 为 []，如果 return了，后面的代码不会运行

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
		backtracking(nums, 0);
		return res;
	}

	public void backtracking(int[] arr, int startIndex){
    	if (startIndex <= arr.length){
    		res.add(new ArrayList<>(list));	//	第一次 就收集到了 []
		}
		for (int i = startIndex; i < arr.length; i++) {
			list.add(arr[i]);
			backtracking(arr, i + 1);
			list.remove(list.size() - 1);
		}
	}
}

image-20230828111429674

90. 子集Ⅱ【先排序，后去重】

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
		Arrays.sort(nums);
    	backtracking(nums, 0);
    	return res;
    }
	public void backtracking(int[] arr, int startIndex){
		if (startIndex <= arr.length){
			res.add(new ArrayList<>(list));	//	第一次 就收集到了 []
		}
		for (int i = startIndex; i < arr.length; i++) {
			list.add(arr[i]);
			backtracking(arr, i + 1);
			list.remove(list.size() - 1);
			while (i < arr.length - 1 && arr[i + 1] == arr[i]){
				i++;
			}
		}
	}
}

491. 递增子序列

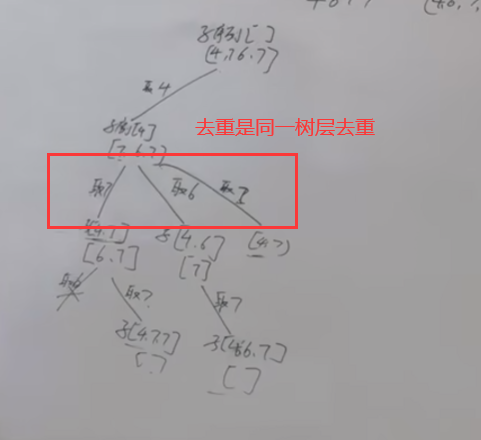
image-20230828153559054

但是同一树枝上是可以重复取的，其实也没有重复取，它取的是不同的元素，仅仅是不同的元素数值相同而已

前面的 7 下的所有分支，一定包含了后面的 7 的所有分支

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();

	public List<List<Integer>> findSubsequences(int[] nums) {
		backtracking(nums, 0);
		return res;
    }

	public void backtracking(int[] arr, int startIndex){
		if (startIndex <= arr.length && list.size() >= 2){
			res.add(new ArrayList<>(list));	//	第一次 就收集到了 []
		}
		Set<Integer> set = new HashSet<>();	//	每一层都用 set 去重
		for (int i = startIndex; i < arr.length; i++) {
			if (isMore(arr[i]) && set.add(arr[i])){
				list.add(arr[i]);
			}else {
				continue;
			}
			backtracking(arr, i + 1);
			list.remove(list.size() - 1);
		}
	}

	public boolean isMore(int num){
    	if (list.size() == 0){
    		return true;
		}
		Integer integer = list.get(list.size() - 1);
    	return (num - integer) >= 0;
	}
}

46. 全排列【强调元素顺序】

看下排列和组合的区别？？？

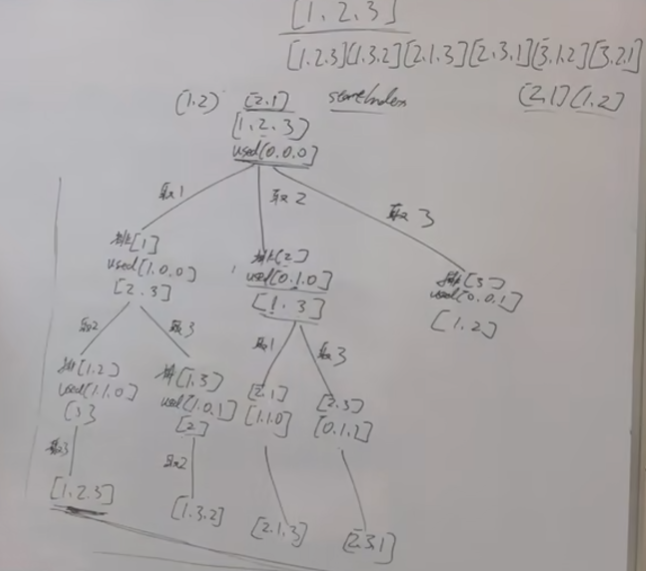
image-20230828193556279

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();
	int[] used;

	public List<List<Integer>> permute(int[] nums) {
		used = new int[nums.length];
		backtracking(nums);
		return res;
    }

    public void backtracking(int[] arr){
		if (list.size() == arr.length){
    		res.add(new ArrayList<>(list));
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			if (used[i] != 1) {
				list.add(arr[i]);
				used[i] += 1;
			}else {
				continue;
			}
			backtracking(arr);
			list.remove(list.size() - 1);
			used[i] = 0; //	回溯
		}
	}
}

47. 全排列Ⅱ（有重复的）

class Solution {
	List<Integer> list = new ArrayList<>();
	List<List<Integer>> res = new ArrayList<>();
	int[] used;

	public List<List<Integer>> permuteUnique(int[] nums) {
		used = new int[nums.length];
		Arrays.sort(nums);	//	先排序
		backtracking(nums);
		return res;
    }

	public void backtracking(int[] arr){
		if (list.size() == arr.length){
			res.add(new ArrayList<>(list));
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			if (used[i] != 1) {
				list.add(arr[i]);
				used[i] += 1;
			}else {
				continue;
			}
			backtracking(arr);
			list.remove(list.size() - 1);
			used[i] = 0; //	回溯
			while (i < arr.length - 1 && arr[i + 1] == arr[i]){
				i++;
			}
		}
	}
}

标签：arr,return,int,list,backstracking,回溯,new,backtracking
From： https://www.cnblogs.com/aclq/p/17664449.html

相关文章

  • LeetCode题库77.组合——dfs典型解法，递归+回溯+剪枝
     classSolution:defcombine(self,n:int,k:int):nums=[x+1forxinrange(n)]res,ans=[],[]defdfs(nums:list[int]):iflen(ans)==k:ans_copy=ans.copy()#复制，避免ans数组改变使res跟着改变......
  • 【LeetCode回溯算法#12】二叉树的直径，树形dp的前置内容（使用dfs）
    二叉树的直径给你一棵二叉树的根节点，返回该树的直径。二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点root。两节点之间路径的长度由它们之间边数表示。示例1：输入：root=[1,2,3,4,5]输出：3解释：3，取路径[4,2,1,3]或......
  • [代码随想录]Day26-回溯算法part06
    题目：332.重新安排行程思路：其实这里已经是图的部分了，回溯应该也可以。Hierholzer算法解决欧拉问题代码：funcfindItinerary(tickets[][]string)[]string{var(m=map[string][]string{}res[]string)for_,ticket:=rangeticket......
  • [代码随想录]Day25-回溯算法part05
    题目：491.递增子序列思路：核心问题——同层去重，这一题不能够重新排序因此不可以用i>index&&nums[i]==nums[i-1]来去重，而是每一层开一个map来判断该数是否出现过代码：var(res[][]intpath[]int)funcfindSubsequences(nums[]int)[][]int{res=make(......
  • [代码随想录]Day24-回溯算法part04
    题目：93.复原IP地址思路：函数参数：参数就一个stirng，path先收集ip地址的四个部分，最后存入res中时拼接成一个string,因此path和res都是[]string类型终止条件：当path有了ip的四个部分就终止；当然只有完全的把字符串遍历了才会存入res单层逻辑：先取1-3位，判断是不是0-255内的数并且没......
  • 利用PCRE回溯次数限制绕过安全限制
    第一部分：正则表达式和回溯基础1、正则表达式概述正则表达式是一种用于匹配字符串模式的工具。其在文本搜索、数据验证等方面具有强大的应用。在匹配的过程中，会使用有限状态自动机的概念，包括确定性有限状态自动机（DFA）和非确定性有限状态自动机（NFA）。2、回溯的过程正则引擎使用回......
  • [代码随想录]Day22-回溯算法part02
    题目：216.组合总和III思路：多加一个记录和的参数，还有一个起始位置的参数(不重复就得加)结束条件是个数到了k：如果此时sum==n那就说明答案正确如果此时sum!=n那就直接返回剪枝的话：如果之后的和大于n那就没必要继续遍历了代码：varres[][]int//答案varpath[]int......
  • [代码随想录]Day21-回溯算法part01
    题目：77.组合思路：回溯就是dfs的一个特殊情况也就是递归的一种情况，值得注意的一点：要记得深拷贝，不然最后全是空代码：varres[][]intvarpath[]intfunccombine(nint,kint)[][]int{res=[][]int{}path=make([]int,0,k)Combine(n,1,k,0)ret......
  • 基础算法之搜索与回溯算法C++
    1、组合的输出【题目描述】排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r≤n)，我们可以简单地将n个元素理解为自然数1，2，…，n，从中任取r个数。现要求你用递归的方法输出所有组合。例如n＝5，r＝3，所有组合为：12312412513413514523......
  • [算法考研笔记]mm算法随笔[成绩划分][回溯0-1][得分][字段和][聪明小偷][股票买卖]
    mm算法随笔学习笔记（回溯算法）回溯<---->递归1.递归的下面就是回溯的过程回溯法是一个纯暴力的搜索、有的时候暴力求解都没有办法，用回溯可以解决。回溯法解决的问题：组合问题如：1234两两组合切割问题如：一个字符串有多少个切割方式，或者切割出来是回文子集问题：1......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99