首页 > 编程语言 >[算法考研笔记]mm算法随笔[成绩划分][回溯0-1][得分][字段和][聪明小偷][股票买卖]

[算法考研笔记]mm算法随笔[成绩划分][回溯0-1][得分][字段和][聪明小偷][股票买卖]

时间：2023-08-13 11:11:05浏览次数：38  
标签：arr mm max price int 算法 include dp 考研

mm算法随笔

学习笔记（回溯算法）

  1. 回溯 <---->递归1.递归的下面就是回溯的过程

  2. 回溯法是一个 纯暴力的 搜索、有的时候暴力求解都没有办法，用回溯可以解决。

  3. 回溯法解决的问题：

    • 组合问题 如：1234 两两组合
    • 切割问题 如：一个字符串有多少个切割方式 ，或者切割出来是回文
    • 子集问题 ： 1 2 3 4 的子集
    • 排列问题（强调顺序），组合不强调顺序
    • 棋盘问题：n皇后 解数独

  4. 所有回溯法可抽象成树形结构，n叉树

  5. 5. void  backtracking(参数)
{

	if(终止条件)	{

		收集结果 //叶子结点,放入结果集

		return;

	}
	//单层搜索
	
	for(集合的元素集，类似子节点的个数)

	{

		处理结点

		递归函数	 //一层一层往下

		回溯操作	//相当于撤销

	（撤销处理结点12， 2撤销 ，13 撤销3， 14）

	}
	return;
}

所有的回溯法都可以抽象成这样的n叉树

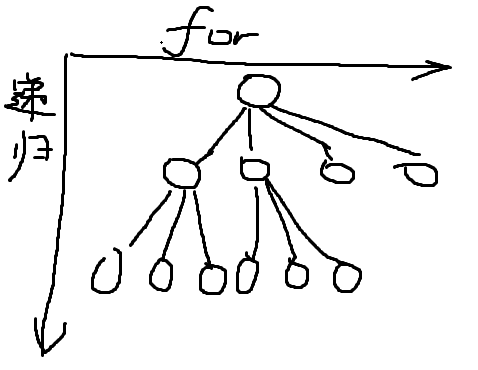
image-20230802114921519

其实回溯算法就是通过递归来控制有多少层for循环

类似1,2,3,4的长度为2的子集
	可以用	for(i=1;i<size;i++){
		for(j=i+1;j<size;j++){}
	}
	得出
1-10的长度为3的
	可以嵌套3层
	for(i=1;i<size;i++){
		for(j=i+1;j<size;j++){
			for(z=j+1;z<size;z++){}
		}
	}
但是如果要100个数找50的
就不可能
for(){
	for(){
		for(){
			for....

所以回溯算法通过递归控制for的层数

回溯法和分支限界的区别

方法 回溯法 分支限界
对解空间树的搜索 深度优先 广度优先或者最小耗费优先
存储结点的常用数据结构 堆栈 队列优先队列
结点存储特性 活结点的所有可行子节点被遍历后才弹出 每个结点只有一次成为活接点
常用应用的最优解 找出满足约束条件的所有解 找出满足约束条件的一个解或特定解

算法题目随笔

1.成绩划分问题

给你⼀组学⽣的成绩(整型)，要求将其划分成若⼲个集合。每⼀集合内学⽣相邻分数不超过x,你有k个学⽣（分数任 意）可以插⼊到这组成绩中。问最少可以将此组成绩划分成多少个集合。（例如x=3,{3,6,7,9,15,18,19}可以划 分成两个集合(3,6,7,9),(15,18,19)）。

#include<iostream>
#include<algorithm>
#define maxn 100
using namespace std;

int x,k;
int num[maxn];

bool cmp(int a,int b){
	return a<b;
}

int main(){
	cin>>x>>k;
	for(int i=0;i<k;i++){
		cin>>num[i];
	}
	sort(num,num+k,cmp);
	
	for(int i=0;i<k;i++){
		cout<<num[i]<<" ";
		if(num[i] + x < num[i+1] && i<k-1){
			cout<<endl;
		}
	}
	return 0;
}

我感觉不是很对，因为没有用到算法，纯粹是排序加上划分界限。

晚点听课吧

、、、、、、

还真是先排序 （√）

方便分割集合

划分好集合后

\((3,6,7,9)和(15,18,19)\)

再如果k=2的话

两个任意的分数 可以把两个数组串起来

\((15 - 9 -1 )/3 = 1\)

为了确保15和9之间 每个数之间可以为3，所以还要\(15-9-1\)

\((15-9)/3 = 2需要两个，但是真的需要来两个吗？\)

\(3,6,7,9,12,15,18,19\)

满足

所以要用\((15-9-1)/3\)

把这样的断点全部放入一个temp数组

再对temp数组排序，看看中间的缝隙能插入多少来保证插入的最少

//预留更新后的代码
#include <iostream>
#include <algorithm>
using namespace std;
const int Maxn=1e3+7;
int n;
int x;//最大差值不超过x
int arr[Maxn];
int InsertTime[Maxn];//插入次数
int cnt;//分组
int k;//允许插入的学生数
int ans=1;
void fun()
	{
	sort(arr+1,arr+1+n);//从小到大排序
	for(int i=1;i<n;i++)
	{
		if(arr[i+1]-arr[i]>x)
		 {
			InsertTime[++cnt]=(arr[i+1]-arr[i]-1)/x;
		 }
	}
	sort(InsertTime+1,InsertTime+1+cnt);//对插入数组进行排序
	for(int i=1;i<=cnt;i++)//优先对断点处需要少的插入数据进行插入 才能使最后分组最少
	{
		if(k>=InsertTime[i])
		{
			k-=InsertTime[i];
		}
		else
		{
			ans=cnt-i+2;
			break;
		}
	}
}
int main()
{
	cin>>n>>x>>k;
	for(int i=1;i<=n;i++)
		cin>>arr[i];
	void fun();
	cout<<"ans="<<ans<<endl;
	return 0;
}

2.⽤回溯法解决0-1背包问题(加上剪枝操作)

#include<iostream>
#include<algorithm>
#define maxn 100
using namespace std;

int n;
int w,v;
int c;
int bestp = 0;
int cw=0,cv=0;

struct good{
	int w;
	int v;
	int ischosen;
};
good goods[maxn];
bool cmp(good a,good b){
	return a.v/a.w>b.v/b.w;
}

int bound(int t){
	int cleft = c-cw;	//剩余重量 
	int b = cv;	//当前价值
	while(t <= n && goods[t].w <= cleft){
		cleft -=goods[t].w;
		b += goods[t].v;
		t++;
	} 
	if(t<=n){
		b+=goods[t].v/goods[t].w*cleft;
	}
	return b;
}

void backtrack(int t){
	if(t > n){
		goods[t].ischosen = 1;
		bestp = cv;
	}
	if(cw + goods[t].w <= c){	//左子树 
		cw+=goods[t].w;
		cv+=goods[t].v;
		backtrack(t+1);
		cw-=goods[t].w;
		cv-=goods[t].v;
	}
	if(bound(t+1)>bestp){
		backtrack(t+1);
	}
}

int main(){
	cin>>n>>c;
	for(int i=0;i<n;i++){
		cin>>goods[i].w>>goods[i].v;
	}
	sort(goods,goods+n,cmp);
	backtrack(0);
	cout<<bestp;
	return 0;
}

剪枝函数约束函数就是利用了贪心算法里的那个bound / up 上限

想明白左子树是1 是选取 ;右子树是0是，不选取

设计backtrack()

  • t>n 符合要求，ischosen=1,更新bestp
  • 左分支展开 cw + goods[t].w <= c
  • 右分支处理 用限界函数判断要不要生成（因为是0 所以是不装 w和p不用更新）直接用该孩子结点当根节点往下

3.迷宫问题

给你⼀个m⾏n列的迷宫。问你是否可以从起始位置⾛到结束位置(⼈只能按照上下左右四个⽅向位移，并且迷宫有些位 置有墙不能进⼊)。

使用分支限界法+巧用queue!

#include<iostream>
#include<algorithm>
#include<queue> 
#define maxn 100
using namespace std;

int m,n;
int x,y;	//起始点 
int tx,ty;	//终止点 
int arr[maxn][maxn];
int move[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};	//上下左右 

struct node{
	int x;
	int y;
	int step;
};

bool legal(node a){
	if(a.x<1 || a.y<1 || a.x>m || a.y>n)	//越界 
		return false;
	if(arr[a.x][a.y]==1)	//已走过 
		return false;
	return true;
} 

void bfs(){
	queue <node> que;
	node now,next;
	now.x = x;
	now.y = y;
	now.step = 0;	//初始化根节点
	que.push(now);
	while(!que.empty()){
		now = que.front();
		que.pop();
		if(now.x == tx && now.y == ty){	//找到了 
			cout<<"success:"<<now.step<<endl; 
			return ;
		}
		for(int i=0;i<4;i++){	//结点的四方向依次入队 
			next.x = now.x + move[i][0];
			next.y = now.y + move[i][1];
			next.step = now.step + 1;
			
			if(legal(next)){	//如果可以走，用step打上标记 
				que.push(next);	//可以走，则压入
				arr[next.x][next.y] = 1; //做标记防重复 
			} 
		}
	}
}

int main(){
	cin>>m>>n;
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			cin>>arr[i][j];
		}
	}
	cin>>x>>y>>tx>>ty;
	bfs();
	return 0;
}

这个我还是不熟悉

看的答案 跟着答案敲的代码

要找一条路，就用分支限界

设计利用bfs()和队列；

关注子节点是如何生成的：\(在这题里就是上下左右\)，代表依次入队

熟悉#include

关键是熟悉while(!queue.empty())的使用

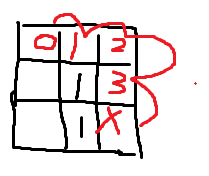
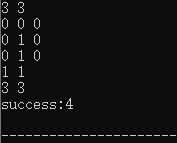
使用方法：image-20230808161836429image-20230808162132903

得分

有⼀队玩家站成⼀列，每位玩家都有⾎量，每位玩家都只能挑战站在他后⾯的所有的玩家，如果他的⾎量⽐他后⾯的 某位玩家⾎量⾼，则他获胜，他能打败的玩家个数也就是他的得分。请设计⾼效的算法求出所有玩家的分和

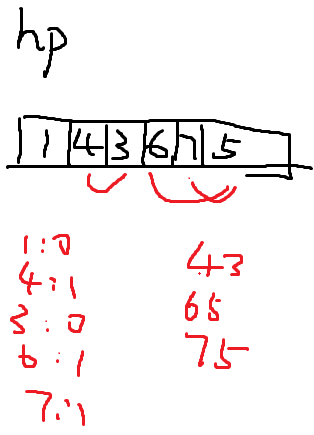
image-20230808162343425

其实就是一个逆序问题

逆序长度为2，找出所有长度为2的逆序个数

排列或者组合用回溯

两个for循环是不是结束了？？？

在count 是一个全局变量，并且它的名字和 C++ 标准库中的一个函数名称冲突了。

注意在c++使用的时候避免使用名为count的变量

回溯实现失败代码,感觉没啥问题但是没法实现

#include<iostream>
#include<algorithm>
#include<stack>
#define maxn 100
using namespace std;

int result=0;
int n;
int num[maxn];
stack <int> st;

void backtrack(int t){
	if(num[t] > st.top() && st.size() == 1){
		result += 1;
		return ;
	}
	for(int i=t;i<n;i++){
		st.push(num[t]);
		backtrack(t+1);
		st.pop();
	}
}

int main(){
	cin >> n;
	for(int i=0;i<n;i++){
		cin>>num[i];
	}
	backtrack(0);
	cout<<result;
	
	return 0;
}

用分治递归？？

先跳过，实在不行用两层for遍历得了（朴素方法，枚举）复杂度n方

逆序对问题

使用分治法

分成左右两边

//
int n;
int arr[Maxn]; //原数组，下标从1到n
int tep[Maxn];
int ans;
void msort(int l,int r)
{
	if(l==r)
		return;
	int mid=(l+r)/2;
	//划分
	msort(l,mid);
	msort(mid+1,r);
	//合并
	int i=l; //指向左半段的开始
	int j=mid+1 //指向右半段的开始
	int k=l; //指向临时数组的开始
	while(i<=mid&&j<=r)
	{
		if(arr[i]<=arr[j])
			tep[k++]=arr[i++];
		else
		{
			tep[k++]=arr[j++];
			ans+=(mid-i+1); //对于arr[j]来说， 左半段的后mid-i+1个元素都?于arr[j]，逆序对增加mid-i+1对
		}
	}
	while(i<=mid)
		tep[k++]=arr[i++];
	while(j<=r)
		tep[k++]=arr[j++];
	for(i=l;i<=r;i++)
		arr[i]=tep[i];
}

最⼤⼦段和分治法

对于数组arr[1.2.3….n]，在数组的任意连续段连续的⼦数组，求和的值最⼤是多少，请⽤分治法。

输⼊：第⼀⾏ n 表示数组⻓度为n

第⼆⾏输⼊n个数字

输出：最⼤⼦段和⻓度

输⼊： 6

​ -1 2 -1 3 -2 1

输出： 4

定名了使用分治法

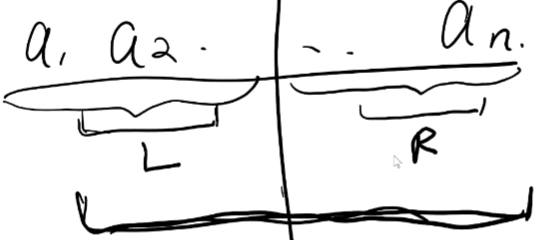
image-20230808171731026

image-20230808171744236

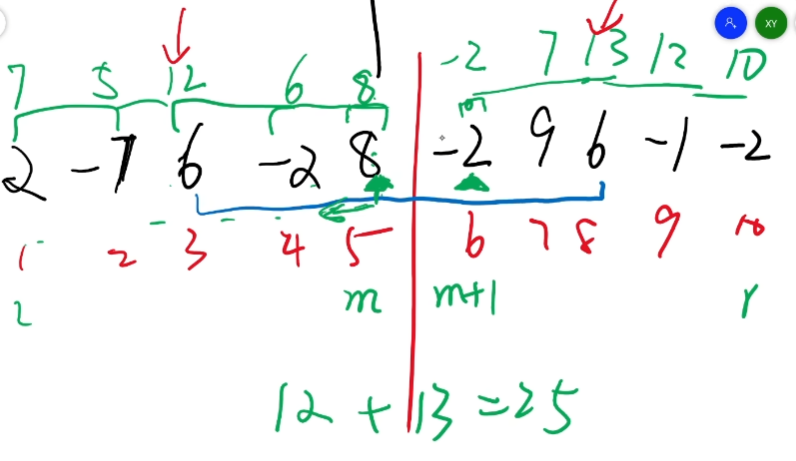
image-20230808171952714

中间一分为2，m往左看，m+1往右看，然后中间一加起来就是最大的25

分治递归的伪代码：

MaxSubSum(A,left,right)
	if |A| == 1 : return A
	mid = (left+right) / 2
	leftsum = MaxSubSum(A,left,mid)
	rightsum = MaxSubSum(A,mid+1,right)

代码实现

#include<iostream>
#include<algorithm>
#include<cmath>
#define maxn 100
using namespace std;

int n;
int arr[maxn];

//找到l-r的横跨左右的最大字段和 
int f(int l,int r){
	int m = (l+r)/2;
	int sumL=0,ansL=arr[m];
	int sumR=0,ansR=arr[m+1];
	for(int i=m;i>l;i--){	//站中间往左看 
		sumL+=arr[i];
		ansL = max(ansL,sumL);
	}
	for(int i=m+1;i<r;i++){	//站中间往右看 
		sumR+=arr[i];
		ansR = max(ansR,sumR);
	}
	return ansL+ansR;
}


int Maxsum(int l,int r){
	if(l==r) return arr[l];
	else{
		int m = (l+r)/2;
		int L = Maxsum(l,m);
		int R =	Maxsum(m+1,r);
		int LR = f(l,r);
		return max(max(L,R),LR);
	}
}


int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>arr[i];
	}
	cout<<Maxsum(0,n-1);
	
	return 0;
}

运行结果：

image-20230808173733470

复杂度\(三重循环：O(n^3),二重循环O(n^2),分治法O(nlogn),动态规划O(n)[一重循环]\)

聪明的小偷

典型动态规划

用已知态、递归基，不断利用已知态推导未知态！

已知态如何转化为未知态的就是利用的状态转移方程

像斐波那契数列的状态转移方程就是\(dp[n] = dp[n-1] + dp[n+2]\)

小偷问题就是

如果你只有一间房image-20230808175834176那就直接偷

如果你有两间房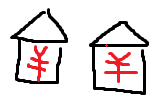image-20230808175911332偷两个中最大的金额

三间房的时候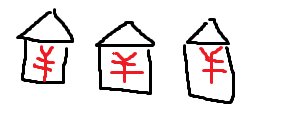image-20230808180025845就可以开始对问题进行分解

偷第一间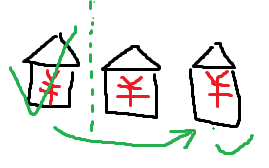image-20230808180205253则第三间也可以偷

不偷第二间则范围又缩小到两间房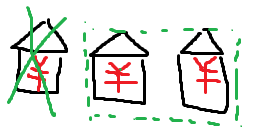image-20230808180347736

通过这种方法，不断用已知的推出未知的，即可完成动态规划的目标

我们假设从后往前开始偷。

从最右端开始逐步迭代这张表

所以循环从n-3项开始，从尾偷到头

所以最大的应该就是arr[0]。

动态规划的思考步骤

  • 明确状态定义，即dp[n]代表什么
  • 确定初始已知态（从简单开始分析）偷一间？偷两间？
  • 确定状态转移方程
  • dp[n] = max(dp[n+1],dp[n+2] + nums[n])

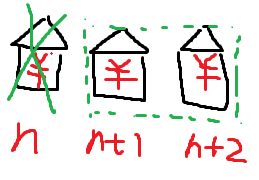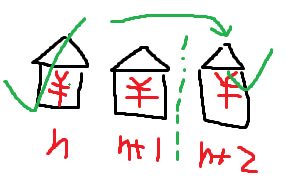
1.image-202308082048021022.image-20230808204839746

就是以上两种情况的最大值

完整代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#define maxn 100
using namespace std;

int n;
int arr[maxn]; 
int steal(int arr[]){
	int dp[n];
	dp[n-1] = arr[n-1];	//末尾的 只有一间房的情况
	if(n > 1) dp[n-2] = max(arr[n-1],arr[n-2]);	//两间房 取最大的偷
	for(int i=n-3;i>=0;i--){
		dp[i] = max(dp[i+1],arr[i] + dp[i+2]);
	} 
	return dp[0];
}

int main(){
	cin >> n;
	for(int i=0;i<n;i++){
		cin>>arr[i];
	}
	cout<<steal(arr);
	return 0;
}

买卖股票最佳时机

给定⼀个数组 prices ，其中 prices[i] 是⼀⽀给定股票第 i 天的价格。设计⼀个算法来计算你所能获取的最 ⼤利润。你可以尽可能地完成更多的交易（多次买卖⼀⽀股票）。注意：你不能同时参与多笔交易（你必须在再次购 买前出售掉之前的股票)

只能买卖一次

\(例如数组[7,1,5,3,6,4]\)

\(结果是5。是第二天买入1 在第5天卖出\)

思路1：大不了两次for循环 \(O(n^2)\)

思路2：动态规划

dp[i][0] 持有股票最大的现金，
dp[i][1] 不持有这支股票的最大现金
【7,1,5,3,6,4】
找dp[n-1][0]
dp[n-1][1]

找递推公式：
前面不变，保持持有股票 dp[i-1][0]
第i天买入了，开始持有了 -price[i]
dp[i][0] = max(dp[i-1][0],  0 -price[i] )	//记住这个0-

前一天是不持有的状态 dp[i-1][1]
第i天卖了 说明前面一天持有！ dp[i-1][0]+price[i]
dp[i][1] = max(dp[i-1][1] , dp[i-1][0]+price[i])


dp[0][0] = -price[0]	//第一天买入
dp[0][1] = 0			//第一天不买入

遍历顺序，根据0的状态往后推
for(i=1;iu<len;i++)
	....
最后找 max(dp[n-1][0] , dp[n-1][1])
其实结果就是 dp[n-1][1] //因为算的是手头的现金 最后一天不管多少钱必卖

打印dp[]

可以多次买卖

\(数组[7,1,5,3,6,4]\)

可以用贪心 但是适用性不高

买卖多次和买卖一次

\(不持有的dp的max是一样的\)

  • 前一天就不持有
  • 当天卖出 + 前一天的现金

这一点和买卖一次思路一致

区别在于dp [i] [0]

即持有的dp，因为买卖多次，第i天我们手头上的现金可能是非0的（前面倒卖的利润）

dp = max(

  • 前一天就持有 dp[i-1] [0]

  • 前一天不持有股票的状态 - price[i] dp[i-1] [1] - price[0]

    )

#include<iostream>
#include<algorithm>
#include<cmath>
#define maxn 100
using namespace std;

int arr[maxn];
int dp[maxn][2];
int result;
int n;

void buysell(){
	dp[0][0] = -arr[0];
	dp[0][1] = 0;
	for(int i=1;i<n;i++){
		dp[i][0] = max(dp[i-1][0] , dp[i-1][1] - arr[i]);
		dp[i][1] = max(dp[i-1][1] , dp[i-1][0] + arr[i]);
	}
	result = dp[n-1][1];
}

int main(){
	cin >> n;
	for(int i=0;i<n;i++){
		cin>>arr[i];
	}
	buysell();
	
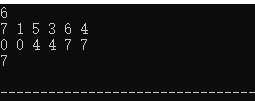
	for(int i=0;i<n;i++){
		cout<<dp[i][1]<<" ";
	}
	
	
	
	cout<<endl<<result<<endl;
	
	return 0;
}

结果分析：

  • 1买5卖 赚4
  • 3买6卖 赚3
  • 一共赚7

image-20230809114817336

限定买卖至多买卖2次

\([3,3,5,0,0,3,1,4]\)

输出6 = 3-0 + 4-1

不要心乱，抓住小方面

  • 明确dp含义
  • 递推公式
  • 初始化
  • 遍历顺序
dp[i][0]	不操作	0
dp[i][1]	第一次持有
dp[i][2]	第一次卖出，不持有	//可能是延续状态，不一定当天
dp[i][3]	第二次持有
dp[i][4]	第二次不持有

//递推公式
dp[i][0] = dp[i-1][0]
dp[i][1] = max(dp[i-1][1] , dp[i-1][0] - price[i])	//延续前一天or当天买入
dp[i][2] = max(dp[i-1][2] , dp[i-1][1] + price[i])	//延续or 当天卖出
dp[i][3] = max(dp[i-1][3] , dp[i-1][2] - price[i])	
dp[i][4] = max(dp[i-1][4] , dp[i-1][3] + price[i])

//初始化
dp[0][0] = 0
dp[0][1] = -price[0]
dp[0][2] = 0
dp[0][3] = -price[0]
dp[0][4] = 0

//遍历循环
for(i=1;i<len;i++)

//输出
max? dp[i][2] dp[i][4]
其实不必
第二次卖出一定是最大值 如果你第一次卖出一件事最大值，再买再卖不影响


### 至多买卖k次

询问最大收入是多少

$[3,3,5,0,0,3,1,4]$

你买卖两次你就列到dp[i] [4]了

有k次的话  dp[i] [2k]

dp数组大小 dp [price.size] [2k+1]

用j （j每次+2） 来控制循环
max( ,)

for(j=0; j<2k ; j+=2)
dp[i][j+1] = max(dp[i-1][j+1] , dp[i-1][j] - price[i])
dp[i][j+2] = max(dp[i-1][j+2] , dp[i-1][j+1] + price[i])

//初始化
dp[0][0] = 0
dp[0][1] = -price[0]
dp[0][2] = 0
dp[0][奇数] = -price[0]
dp[0][偶数] = 0

for(j=1;j<2*k;j+=2)
dp[0][j] = -price[0]




### 股票买卖的最佳时期（含冷冻期）

例子$[1, 2, 3, 0, 2]$

​		买 卖 冷 买 卖

（你卖的后面一天是冷冻期、不许买卖）

输出3

//dp含义
dp[i][0] 持有股票的状态
dp[i][1] 保持卖出股票的状态 //将之前的拆分成 不持有 和 当天卖
dp[i][2] 具体卖出股票的状态 //确定卖的一天，才能知道卖的后一天的冷冻
dp[i][3] 冷冻期

//递推公式
dp[i][0] 延续dp[i-1][0]
买入股票 dp[i-1][3] - price[i] //前一天冷冻期
dp[i-1][1] - price[i] //前一天不是冷冻期，一直没有卖
dp[i][1] 前一天保持dp[i-1][1]
前一天是冷冻期 dp[i-1][3]
dp[i][2] = 前一天持有，当天卖 dp[i-1][0] + price[i]

dp[i][3] 冷冻期的前一天必定是卖出了股票
dp[i-1][2]

//初始化
dp[0][0] = -price[0]
dp[0][1] = 0
dp[0][2] = 0

//遍历顺序
for(i=1;i<len;i++)
````
//输出结果是
dp[pricesize-1][1]
[2]
[3]
这三者中的最大值




### 买卖股票最佳时期（含手续费）

例子$[1,3,2,8,4,9]$

手续费=2

输出8  =  5+3

唯一一个区别就是手续费

==利润小于手续费就不去买了呀==

和买卖2的区别

dp[i][0] 持有
dp[i][1] 不持有

//递推公式
dp[i][0] = max (
延续 dp[i-1][0],
dp[i-1][1] - price[i])
dp[i][1] = max(
延续 dp[i-1][1],
dp[i-1][0] + price[i] (利润) - fee(手续费)
)


### 买卖股票最佳时机问题

总结：

问题1：买卖1次

问题2：买卖多次

问题3：至多2次 列出两次的全部状态

问题4：至多买卖k次 抽象化、泛指

问题5： 含冷冻期 把卖出的状态拆分成两个

问题6：含手续费 和问题2差别不大

标签：arr,mm,max,price,int,算法,include,dp,考研
From： https://www.cnblogs.com/jinwan/p/17626290.html

相关文章

  • 前端开发工程师需要掌握哪些算法？
    一个程序员一生中可能会邂逅各种各样的算法，但总有那么几种，是作为一个程序员一定会遇见且大概率需要掌握的算法。作为一名前端开发工程师，今天就通过这个话题和文章来聊聊前端开发工程师需要掌握的算法有哪些呢。......
  • 基于GMM高斯混合模型的语音信息身份识别算法的matlab仿真
    1.算法理论概述一、引言     语音信息身份识别是指通过声音信号对个体进行身份识别的过程。目前，语音信息身份识别已经成为语音处理领域的一个热门研究方向。在语音信息身份识别中，高斯混合模型（GMM）是一种被广泛应用的方法。本文将详细介绍基于GMM的语音信息身份识别算法的实......
  • 算法——初级排序算法之快速排序
    介绍快速排序可以说是应用最广泛的排序算法了，主要是因为实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。快速排序是一种基于分治思想的排序算法。它将一个数组分成两个子数组，将两部分独立地排序。原理设置两个变量low、high，排序开始时：low=0，hig......
  • acwing 116.飞行员兄弟 (算法竞赛进阶指南 p48 t1 ) 题解
    原题链接https://www.acwing.com/problem/content/description/118/题目描述“飞行员兄弟”这个游戏，需要玩家顺利的打开一个拥有16个把手的冰箱。已知每个把手可以处于以下两种状态之一：打开或关闭。只有当所有把手都打开时，冰箱才会打开。把手可以表示为一个4х4的矩阵，您可以......
  • 算法——初级排序算法之归并排序
    介绍将两个有序的数组归并成一个更大的有序数组，这种算法叫归并排序特点优点：能够保证将任意长度为N的数组排序所需时间和NlogN成正比缺点：所需的额外空间和N成正比1、**原地归并**实现归并的一种直截了当的办法是将两个不同的有序数组归并到每三个数组中，两个数组中的元素......
  • Linux 共享内存mmap,进程通信
    @TOC前言进程间通信是操作系统中重要的概念之一，使得不同的进程可以相互交换数据和进行协作。其中，共享内存是一种高效的进程间通信机制，而内存映射（mmap）是实现共享内存的一种常见方法。一、存储映射I/O存储映射I/O是一个磁盘文件与存储空间中的一个缓冲区相映射。于是，当从缓冲......
  • 压缩算法
    思路因为这个字符串可以被多层压缩，所以我们要找到最里层的中括号。刚开始的思路是利用栈，从前往后找，遇到'['的时候，将元素入栈，遇到']'的时候，让元素出栈，计算出解压后的字符串，然后继续往后遍历，一直到栈为空。但是编码的过程中发现这种办法太过复杂。后来发现，只要从后往前遍历，找到的......
  • 【BP回归预测】基于粒子群算法优化BP神经网络实现数据回归预测附matlab代码
    ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。......
  • 2023-08-12：用go语言写算法。实验室需要配制一种溶液，现在研究员面前有n种该物质的溶液，
    2023-08-12：用go语言写算法。实验室需要配制一种溶液，现在研究员面前有n种该物质的溶液，每一种有无限多瓶，第i种的溶液体积为v[i]，里面含有w[i]单位的该物质，研究员每次可以选择一瓶溶液，将其倒入另外一瓶（假设瓶子的容量无限），即可以看作将两个瓶子内的溶液合并，此时合并的溶液体积和物质含量......
  • 【总结】排序算法的时间复杂度和空间复杂度
    排序算法的时间复杂度和空间复杂度最好时间复杂度最坏时间复杂度平均时间复杂度空间复杂度是否为稳定排序是否为原地排序冒泡排序$O(n)$初始数组正序$O(n^2)$初始数组逆序$O(n^2)$$O(1)$原地使用数组，无额外内存开销是是插入排序是是选择排序$O(n......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99