标签：存储 应用题 元素 矩阵 三角区 数组 对角线 数据结构

数据结构应用题

数组应用题

数组的存储结构

一维数组

A[0...n-1]为例，存储关系

\[LOC(ai)=LOC(a0)+(i)×L(0≤i＜n) \]

L是每个数组元素所占存储单元

多维数组

对于多维数组，有两种映射方法：按行优先和按列优先。

以二维数组为例，按行优先存储的基本思想是：先行后列。
先存储行号较小的元素，行号相等先存储列号较小的元素。
设二维数组行下标与列下标的范围分别为

\[[l1,h1],[l2,h2] \]

，则存储结构关系式为：

\[LOC(a i,j ​ )=LOC(a l 1 ​ ,l 2 ​ ​ )+[(i−l 1 ​ )×(h 2 ​ −l 2 ​ +1)+(j−l 2 ​ )]×L \]

若l1 l2均为0，则上式变成

\[LOC(a i,j ​ )=LOC(a 0,0 ​ )+[i×(h 2 ​ +1)+j)]×L \]

矩阵压缩存储

压缩存储：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。其目的是为了节省存储空间。

特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。常见的特殊矩阵有对称矩阵、上（下）三角矩阵、对角矩阵等。

对称矩阵

任意一个n阶方阵A的任意元素aij=aji,则称为一个对称矩阵。
对于n nn阶方阵，其中的元素可以划分为3个部分，即上三角区、主对角线和下三角区。
对称矩阵上下三角区元素相同，因此存放在一维数组

\[B[n(n+1)/2] \]

中，及aij存放在bk中，只存放主对角线和下三角区（或上三角区）

采用行优先存储，存放主对角线和下三角区

若数组下标从0开始，则在数组B中的下标为

\[k=1+2+3+...+(i-1)+(j-1)=i(i-1)/2+j-1 \]

因此元素下标对应关系

若存放主对角线和上三角区

\[k = n + ( n − 1 ) + . . . + ( n − i + 2 ) + ( j − i ) = ( i − 1 ) ( 2 n − i + 2 ) / 2 + j − i \]

三角矩阵

除了对角线外和上/下三角区，其余的元素都相同

压缩策略：按行优先原则，将三角区和主对角线元素存入一维数组，并在最后一个位置存放常量C

下三角：

上三角：

三对角矩阵

\[∣i−j∣>1时，有Aij=0,呈带状 \]

存储策略：只存储主对角线及其上、下两侧次对角线上的元素外，其他零元素一律不存储。

需要用一个一维数组B 来存储三对角矩阵中位于三对角线上的元素。同样要区分两种存储方式：即行优先方式和列优先方式。

行优先：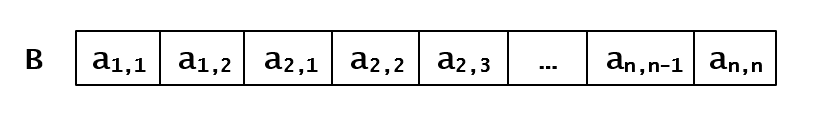

那么数组B中，位于Aij（i<=j)，前边的元素个数为

\[k = 2 + 3 ( i − 2 ) + j − i + 1 = 2 i + j − 3 （数组下标从0开始） \]

于是有对于i的求法，详细如下

\[\begin{align} &前i-1行有3(i-1)+1个元素\\ &前i行共有3i-1个元素\\ &B数组下标为k的元素是第k+1个\\ &3(i-1)+1<k+1<=3i-1\\ &即3(i-1)+1<=k<3i-1\\ &i=⌊(k+1)/3+1⌋ \end{align} \]

标签：存储,应用题,元素,矩阵,三角区,数组,对角线,数据结构
From： https://www.cnblogs.com/cs-gzh/p/16748417.html