模拟退火算法应用举例
这是一篇笔记,是对于B站up主马少平的视频(第四篇 如何用随机方法求解组合优化问题(七))的学习与记录。
旅行商问题
一个商人要访问 \(n\) 个城市,每个城市访问一次,并且只能访问一次,最后再回到出发城市。
问如何规划才能使得行走的路径长度最短。
旅行商问题的解空间非常大,难以使用穷举法进行求解。
- 10城市:\(10!=3628800\)
- 20城市:\(20!\approx 2.43\times 10^{18}\)
在已知模拟退火算法的基本框架,以及需要确定的参数的情况下,为了解决实际问题,我们需要将实际问题,转换并抽离出我们需要的参数。
指标函数
\[f(\pi_1,\cdots,\pi_n)=\sum\limits_{i=1}^nd_{\pi_i\pi_{i+1}}\quad\quad \pi_{n+1}=\pi_1 \]其中 \((\pi_1,\cdots,\pi_n)\) 是表示路径的序列,\(\pi_i\) 表示第 \(i\) 个访问的城市,\(d_{\pi_i\pi_i+1}\) 是路径中相邻两个城市的距离。
新解的产生
逆序交换法
- 当前解
- 交换后
即 \(\pi_u\) 和 \(\pi_v\) 这两个城市之间的路径进行逆序, \(\pi_u\) 和 \(\pi_v\) 不变。
指标函数差
当新解是较好的解时,百分之百接受;当新解是较差的解时,则按概率接受:
\[P_{i\Rightarrow j}(t)=e^{-\frac{f(j)-f(i)}{t}}=e^{-\frac{\Delta f}{t}} \]为了计算接受概率,需要先计算指标函数差 \(f(j)-f(i)\)。
需要注意的是,这里并不需要完全计算出两个解的总路径长度再做差。
由于我们使用的是逆序交换法,两个解之间的差别只存在于逆序区间的交界处。
当前解:\((\pi_1,\cdots,\pi_u,\pi_{u+1},\cdots,\pi_{v-1},\pi_v,\cdots,\pi_n)\)
交换后:\((\pi_1,\cdots,\pi_u,\pi_{v-1},\cdots,\pi_{u+1},\pi_v,\cdots,\pi_n)\)
因此,有:
\[\begin{align*} \Delta f &= f(j) - f(i) \\ &= (d_{\pi_u\pi_{v-1}}+d_{\pi_{u+1}\pi_v})-(d_{\pi_u\pi_{u+1}}+d_{\pi_{v-1}\pi_v}) \end{align*} \]故从解 \(i\) 到解 \(j\) 的接受概率:
\[P_{i\Rightarrow j}(t)= \begin{cases} 1 & if \ \Delta f\le 0 \\ e^{-\frac{\Delta f}{t}} & else \end{cases} \]参数确定
- 初始温度:\(t_0=200\)
- 温度衰减系数:\(\alpha=0.95\),\(t_{k+1}=\alpha t_k\)
- 每个温度下的迭代次数:\(100n\),\(n\) 为城市数
- 算法结束条件:无变化控制法(相邻两个温度下结果相等)
代码实现
测试数据
这里提供了 10 个城市的 xy 坐标。
A 0.4000 0.4439
B 0.2439 0.1463
C 0.1707 0.2293
D 0.2293 0.7610
E 0.5171 0.9414
F 0.8732 0.6536
G 0.6878 0.5219
H 0.8488 0.3609
I 0.6683 0.2536
J 0.6195 0.2634
City class
定义 City 类,方便后续操作。
class City:
def __init__(self, name: str, x: float, y: float):
self.name = name
self.x = x
self.y = y
def __repr__(self):
return f"{self.name} {self.x} {self.y}"
def __str__(self):
return f"{self.name} {self.x} {self.y}"
def distance(self, other: 'City'):
d = ((self.x - other.x)*(self.x - other.x)
+ (self.y - other.y)*(self.y - other.y))**0.5
return d
读取数据
假设上面的测试数据保存在10.txt文件中。这里用一个函数来读取文件数据,并转换为 City 列表。
def read_data(path: str):
data: list[City] = []
with open(path, 'r', encoding='utf-8') as f:
for line in f.readlines():
information = line.replace('\n', '').split(' ')
data.append(City(name=information[0], x=float(information[1]), y=float(information[2])))
return data
生成随机序列
为了随机地生成一个初始解,使用一个数值列表表示旅行商的城市访问顺序:
def gen_random_seq(length: int)->list[int]:
sequence = list(range(length))
random.shuffle(sequence)
return sequence
实现对序列片段的逆序交换
为了生成邻居解,需要实现逆序交换,函数需要传入:原序列、逆序区间的起始下标、结束下标。
def reverse_seq(sequence: list[int], start_idx: int, end_idx: int)->list[int]:
assert start_idx <= end_idx
i = start_idx
j = end_idx
while i<j:
sequence[i], sequence[j] = sequence[j], sequence[i]
i += 1
j -= 1
return sequence
生成邻居解
根据传入的原序列,使用逆序交换法生成邻居解,逆序区间是随机的。
这里生成两个端点a,b之后,进行逆序,但是逆序操作并不包含这两个端点。
因为类似于[0,...,9]和[9,...,0]这两个序列在旅行商问题中是一样的,路线是首尾相接的环。
def gen_near_seq(sequence:list[int])->(list[int], int, int):
n = len(sequence)
a = math.floor(random.random()*n)
b = math.floor(random.random()*n)
start_idx, end_idx = (a, b) if a<b else (b, a)
# 除去区间端点
if end_idx - start_idx > 1:
start_idx += 1
end_idx -= 1
return reverse_seq(sequence, start_idx, end_idx), start_idx, end_idx
指标函数
根据序列和城市列表,计算路径的总长度。
def valuate(sequence: list[int], cities: list[City])->float:
total: float = 0
length = len(cities)
for idx in range(length):
curr_city = cities[sequence[idx]]
next_city = cities[sequence[(idx+1)%length]]
d = curr_city.distance(next_city)
total += d
return total
最终实现
根据上面已经编写好的函数,开始结合算法解决问题。
数据读取
# 文件的路径根据实际情况进行填写
cities = read_data('./dataset/10.txt')
超参数设置
# 初始温度
t = 200
# 温度递减速率
alpha = 0.95
# 问题规模(10个城市)
n = 10
# 同一温度的迭代次数
iteration_times = 100 * n
生成随机序列
随机地生成当前的序列和它的指标:curr_seq和curr_val;
初始化最优解的序列和指标:best_seq和best_val.
curr_seq: list[int] = gen_random_seq(n)
curr_val: float = valuate(curr_seq, cities)
best_seq: list[int] = list()
best_val: float = float('inf')
内外循环
while curr_val != best_val:
i = 0
while i < iteration_times:
i += 1
# 生成相邻解
new_seq, start_idx, end_idx = gen_near_seq(curr_seq)
new_val = valuate(new_seq, cities)
# 是否接受解
if new_val <= curr_val:
curr_seq, curr_val = new_seq, new_val
else:
if random.random() < math.e ** ((curr_val - new_val) / t):
curr_seq, curr_val = new_seq, new_val
# 记录当前温度的最优解
if curr_val < best_val:
best_seq, best_val = curr_seq, curr_val
t *= alpha
运行结果与相关图像
上述 10 个城市的案例,最终结果为
best_val: 2.6906706370094136
通过在上面代码的循环中嵌入“导出数据到csv文件”的操作(这里没有给出代码),然后结合pandas和matplotlib等库,可以绘制出下面图像:
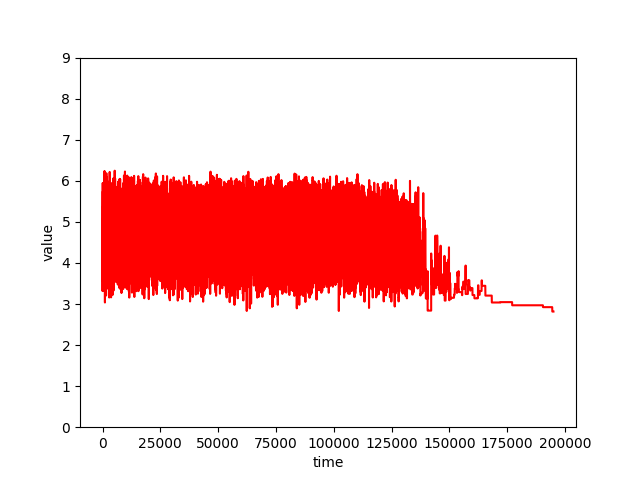
这个图像的横坐标是迭代次数,纵坐标是指标(即路径长度)。
上图的横坐标数据中,每一个温度记录10000个数据,直到最终满足外循环的结束条件。
可以看到,随着温度的下降,波动在变小,并最终收敛到最优解。
前段区间的波动一致,是因为指标本身存在上下界,即十个城市的坐标确认后,最优解和最差解是固定的。
通过减少数据导出频率(提高运行速度),并且将温度的数值进行等比例缩小。将温度和指标绘制到下面这幅图:
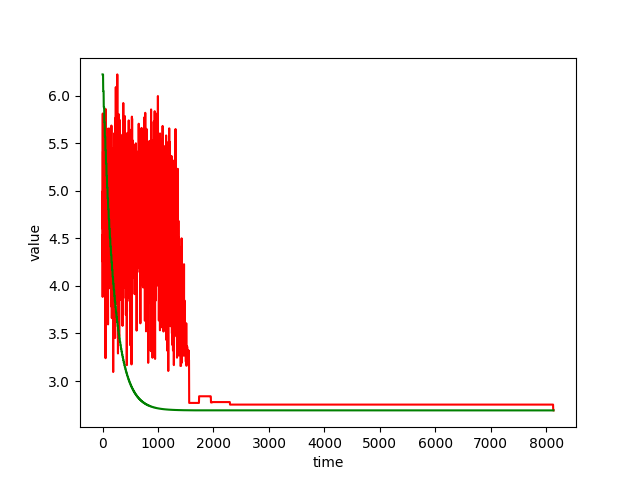
可以更直观地看出温度和指标波动的关系。
标签:seq,idx,求解,int,self,cdots,随机,pi,优化 From: https://www.cnblogs.com/feixianxing/p/combinatorial-problem-random-method-solution-7.html