上一章介绍的KF及其衍生物都在处理容易用参数描述的概率分布(主要是高斯),对于参数化的分布,上述方法能给出解析形式的估计;对于非线性的运动模型与测量模型,上述方法通过线性化等方式也能给出近似的解析估计。但现实中的分布显然还有很多是不容易用参数描述的,且大多数也不是线性模型,这时候想给解析解也比较困难,于是就又有人提出了能提供数值形式估计的贝叶斯滤波器,其中两个便是:直方图滤波和粒子滤波。
直方图滤波
概述:直方图滤波将状态空间分割成了个数有限且离散的子空间(也就是讨论的随机变量值域的一个子集),并在各个离散的子空间中使用均匀分布代替原分布。当原始的状态空间中的元素本来个数就有限时,这个滤波方法也称为离散贝叶斯滤波(Discrete Bayes Filters);当原始的状态空间连续的时候,这个滤波方法则称为直方图滤波(Histogram Filters)。
离散贝叶斯滤波
算法伪代码:
\[\begin{aligned} 1:\quad&\textbf{Algorithm Discrete\_Bayes\_filter(}\{p_{k,t-1}\},u_t,z_t\textbf{):}\\ 2:\quad&\quad \text{for all}\ k\ \text{do}\\ 3:\quad&\quad\quad\bar p_{k,t}=\sum\limits_ip(x_{k,t}|u_t,x_{i,t-1})p_{i,t-1}\\ 4:\quad&\quad\quad p_{k,t}=\eta p(z_t|X_t=x_k)\bar p_{k,t}\\ 5:\quad&\quad \text{endfor}\\ 6:\quad&\quad\text{return}\ \{p_{k,t}\} \end{aligned} \]- 因为状态空间中的元素个数本来就有限,所以离散贝叶斯直接对每个可能的状态做贝叶斯滤波。
- \(\bar p_{k,t}\)多半不是概率,因为此时没有做归一化,不过因为在第4行做了归一化所以\(p_{k,t}\)是概率。
直方图滤波
-
后验估计算法:按照上文所说,直方图滤波将连续的状态空间分解成若干子空间,并在各个子空间上用均匀分布代替原分布。类比离散贝叶斯滤波,直方图滤波中的\(p_{k,t}\)用概率密度再第\(k\)个子空间的积分替代,\(x_{k,t}\)用第\(k\)个子空间上状态变量的均值替代,在各个子空间大小相等的条件下,替代后即可利用离散贝叶斯滤波来进行后验估计。
-
这个算法貌似就是用离散化的卷积运算,代替了原来不好求得连续概率分布的卷积运算,和不好求曲线包围的面积,就把它切成一个个矩形再求和一个道理。
-
对于状态空间是全空间得分布来说显然也没法拆成有限的“格子”,这个时候应该就只有寄希望于过程中密度函数会一直集中于切过格子的地方了。
-
-
分解状态空间的方法:最先想到的肯定就是把比较可能取到的状态空间均分,但这样做有一个显然的问题就是精度和计算速度的冲突会很大,想要高精度就要尽可能细分,而细分肯定就会算的很慢。一个改进的方法称为密度树(Density Tree),它先按粗糙的分法做后验估计,然后对于后验估计概率大的区域再做细分,这样可以避免把计算资源浪费在概率小、对结果影响不大的区域上。这时要注意的一点是因为各个区域的大小\(|\mathbf x_{k,t}|\)不一致了,所以需要将离散贝叶斯滤波的第3行做一个修正(具体推导还是看书4.1.3节)。
\[p_{k,t}=\sum\limits_i|\mathbf x_{k,t}|p(x_{k,t}|u_t,x_{i,t-1})p_{i,t-1} \]
静态状态变量的二值贝叶斯滤波
在这种情况下,需要从传感器数据估计一些不随时间变化的、且只有两种取值的量,比如要知道某个地方是否有一面墙。在构建栅格地图(Occupancy Grid Maps)时也经常需要讨论这一问题。
-
因为讨论的是静态变量,所以不用考虑控制量\(u\)的影响,只用考虑新的测量值\(z\)对估计的影响
-
对数机率比(Log Odds Ratio)来:假设待讨论的状态是\(x\),为了将\(0\sim1\)的范围扩大以方便讨论,常用对数几率比来讨论状态发生的可能性,其定义和图像如下:
\[l(x):=log\frac{p(x)}{1-p(x)} \]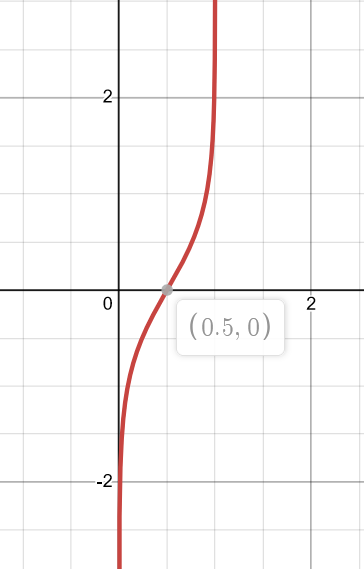
根据对数几率比的定义,不难求出估计:
\[l_t=\frac{\operatorname{bel}_t(x)}{1-\operatorname{bel}_t(x)}\\ \Rightarrow \operatorname{bel}_t(x)=1-\frac{1}{1+\exp(l_t)} \]所以能求出使用测量值\(z_t\)更新\(l_t(x)\)的迭代公式就好了。书上4.2节给出了推导,结论是:
\[l_t=l_{t-1}+\log\frac{p(x\mid z_t)}{1-p(x\mid z_t)}-\log\frac{p(x)}{1-p(x)} \]粒子滤波
粒子滤波同样是求估计的数值解的方法,不同于直方图滤波中类似微积分的思路,粒子滤波使用的是概率的思路。基本算法如下:
\[\begin{aligned} 1:\quad&\textbf{Algorithm Particle\_filter(}\mathcal X_{t-1},u_t,z_t\textbf{):}\\ 2:\quad&\quad\bar{\mathcal X}_{t}=\mathcal X_{t}=\emptyset\\ 3:\quad&\quad\text{for}\ m=1\ \text{to}\ M\ \text{do}\\ 4:\quad&\quad\quad\text{sample}\ x_t{[m]}\sim p(x_t\mid u_t,x_{t-1}^{[m]})\\ 5:\quad&\quad\quad w_t^{[m]}=p(z_t\mid x_t^{[m]})\\ 6:\quad&\quad\quad \bar{\mathcal X}_{t}=\bar{\mathcal X}_{t}+\langle x_t^{[m]},w_t^{[m]}\rangle\\ 7:\quad&\quad \text{endfor}\\ 8:\quad&\quad\text{for}\ m=1\ \text{to}\ M\ \text{do}\\ 9:\quad&\quad\quad\text{draw}\ i\ \text{with probability}\propto w_t^{[i]}\\ 10:\quad&\quad\quad\text{add}\ x_t^{[i]}\ \text{to}\ \mathcal X_t\\ 11:\quad&\quad \text{endfor}\\ 12:\quad&\quad\text{return}\ \mathcal X_t \end{aligned} \]- 输入:上一个时刻的粒子集合\(\mathcal X_{t-1}\)(一个“粒子”对应一个随机生成的状态),控制量\(u_t\),测量值\(z_t\)。
- 第6行的尖括号只是说把\(x_t^{[m]}\)和\(w_t^{[m]}\)打包成了一个元素,然后放入了\(\bar{\mathcal X}_t\)。
- 第9行的“draw”是抽取的意思(相对熟悉的是drawer (n.)抽屉),\(8\sim11\)行(也被称为重采样(resampling)或重要性采样(importance sampling))说的是按照\(\omega_t\)的大小,从\(\mathcal{\bar X}_t\)中抽取\(M\)次\(x_t\)到\(\mathcal X_t\),注意这是会“放回的”的抽取,所以\(\mathcal X_t\)中的元素很可能有不少一样的。
在实现粒子滤波时,要注意一下几个方面
-
从粒子集中恢复概率密度函数:有几种方法
- 高斯:直接用所有粒子求均值方差进行估计
- k-means聚类:To be continued
- 直方图:把状态空间切块,然后按落入子空间的粒子数画直方图
- 核密度估计(Kernel Density Estimation):To be continued
-
重采样导致粒子多样性下降
因为\(8\sim11\)行的重采样正比于权重\(w_t^{[m]}\)且又放回,这就导致高概率的粒子可能会被多次筛出而低概率的粒子可能根本筛不出,粒子的多样性低了,估计也就不会太准确。典型的解决思路有二:
-
降低重采样的频率
-
采用low variance sampling算法:示意如图

假设有\(M\)个粒子,该算法首先把各个粒子的\(w_t^{[m]}\)排在一起,其和为1,也即上图中的矩形框从一头到另外一头是1。开始时生成一个范围在\(0\sim1/M\)的随机数\(r\),它指向之前排好的\(w_t^{m}\)序列并得到第一个采样值,然后往后每隔\(1/M\)再采一次,即可得到新的序列。
该算法既保证了粒子被选出来的概率与权重正相关,又避免了因为筛出权重大的粒子太多次而影响多样性。
-
-
粒子滤波失效:因为是基于概率的算法,所以也会按概率失效。粒子越多出现失效的可能也就会越小。