(十五)MIT公开课雷达系统工程之杂波抑制(多普勒处理)

0 写在前面

岁月静好是片刻，一地鸡毛是日常，即使世界偶尔薄凉，内心也要繁华似锦，浅浅喜，静静爱，深深懂得，淡淡释怀，望远处的是风景，看近处的才是人生，唯愿此生，岁月无恙；只言温暖，不语悲伤。——杨绛

1 基本介绍

问题：不仅仅是地杂波。一个陷波为零的多普勒滤波器不能充分抑制雨杂波。

MTI对消器的问题：通常，它们一次处理几个（2-5）个脉冲，所以如果滤波器的输入为8-10个脉冲，那么几乎不可能像你所能的那样对它们进行整形：2脉冲MTI消除器在多普勒空间中非常宽。使用8-10个脉冲的一组通带多普勒滤波器）可以被构造为具有：零多普勒陷波抑制地面杂波；一组通带滤波器，可以检测是否有雨杂波。在20世纪70年代中期之前，还没有对同时对出现的地面和雨水杂波进行成本效益高的脉冲多普勒解决方案的技术。

2 问题视角

Utility of Burst Waveforms for Clutter Rejection：这些样本可以通过一组通带滤波器进行线性处理：检测多普勒速度范围内的目标，同时抑制低旁瓣杂波；如果带通滤波器的频率足够窄，则可以测量通过它们的目标的多普勒速度。

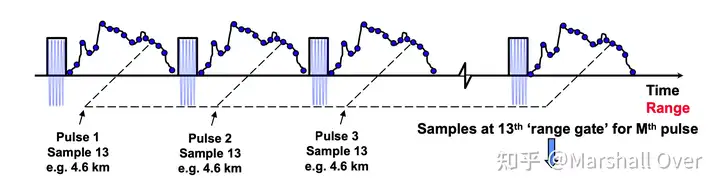
Impact of Moore’s Law of Radar Processing：

3 脉冲多普勒处理技术

3.1 脉冲多普勒处理

脉冲多普勒处理波形回顾:

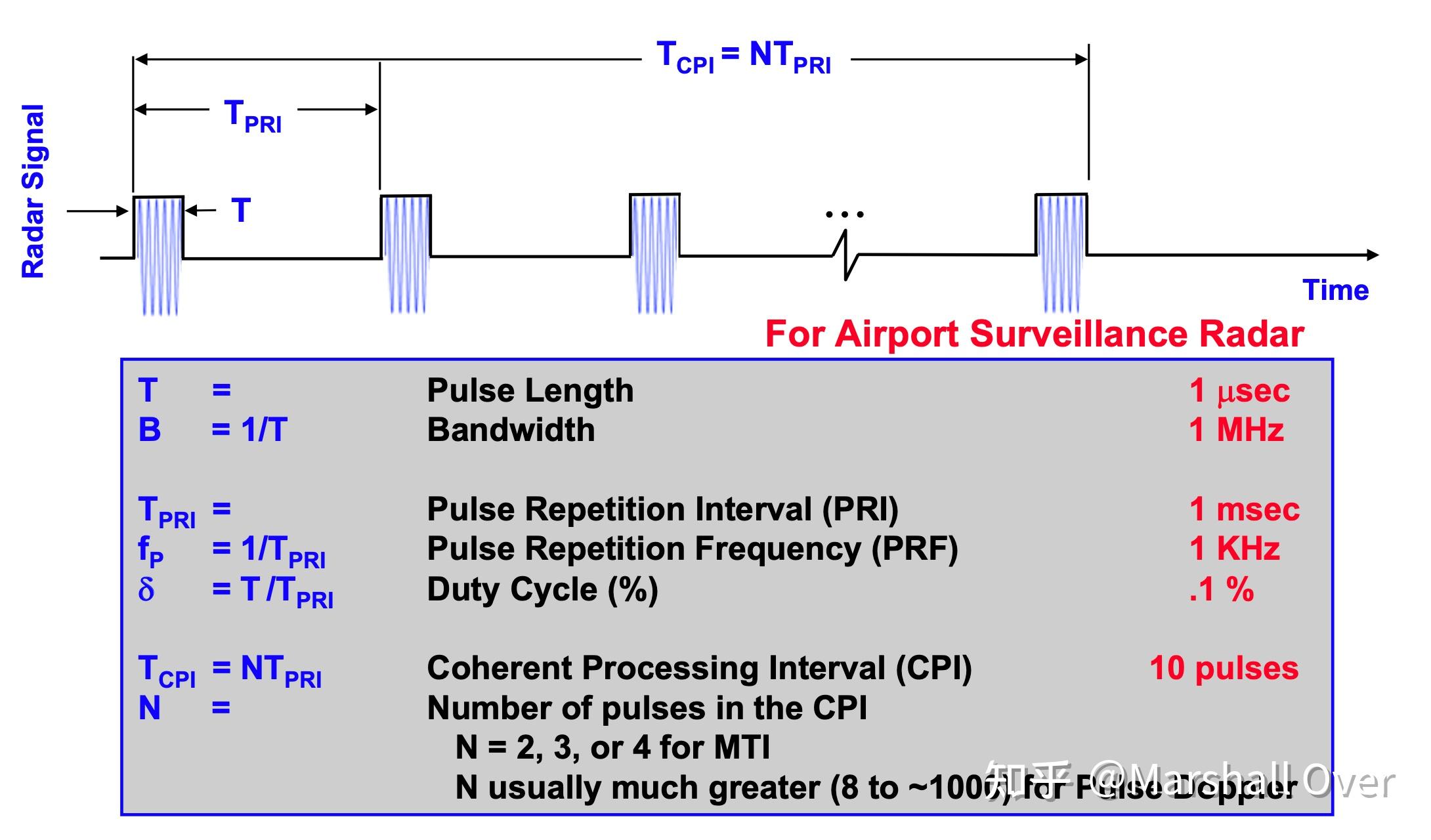
用于多普勒处理的数据收集：

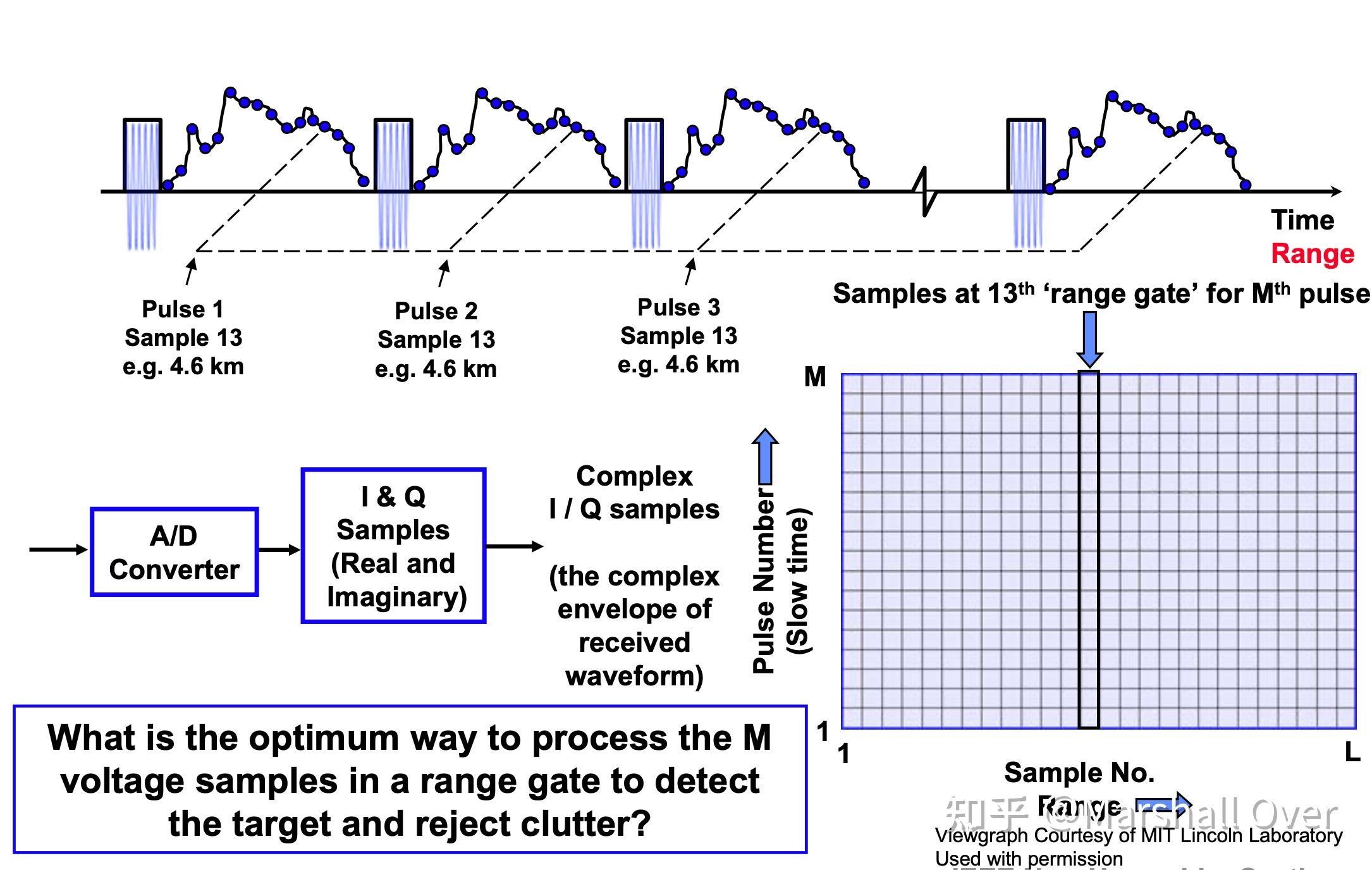
Pulse Doppler Processing - Cartoon：

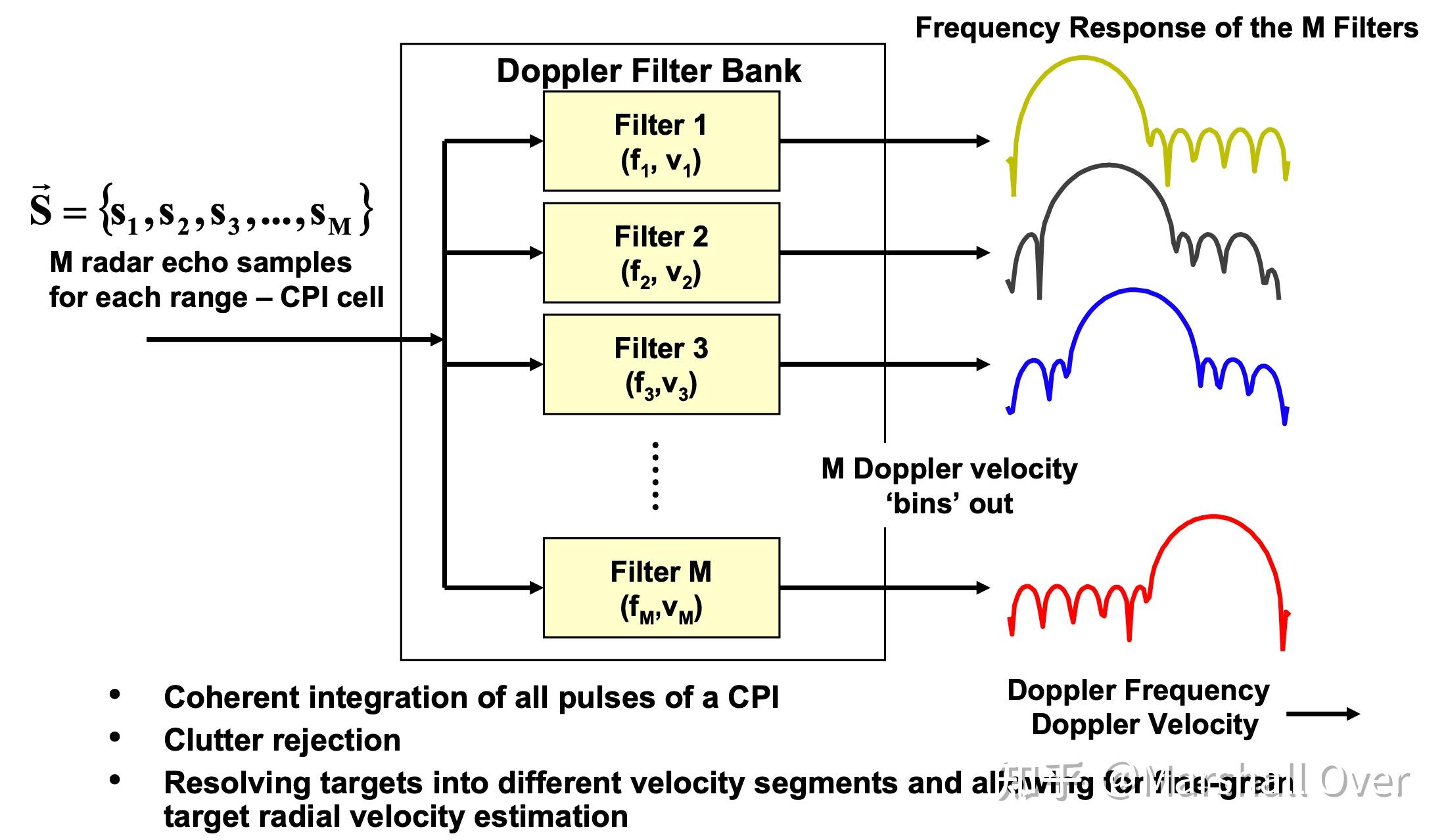
脉冲多普勒处理的优化：

最佳MTI改善系数：

脉冲多普勒处理：

MTI改善系数比较：

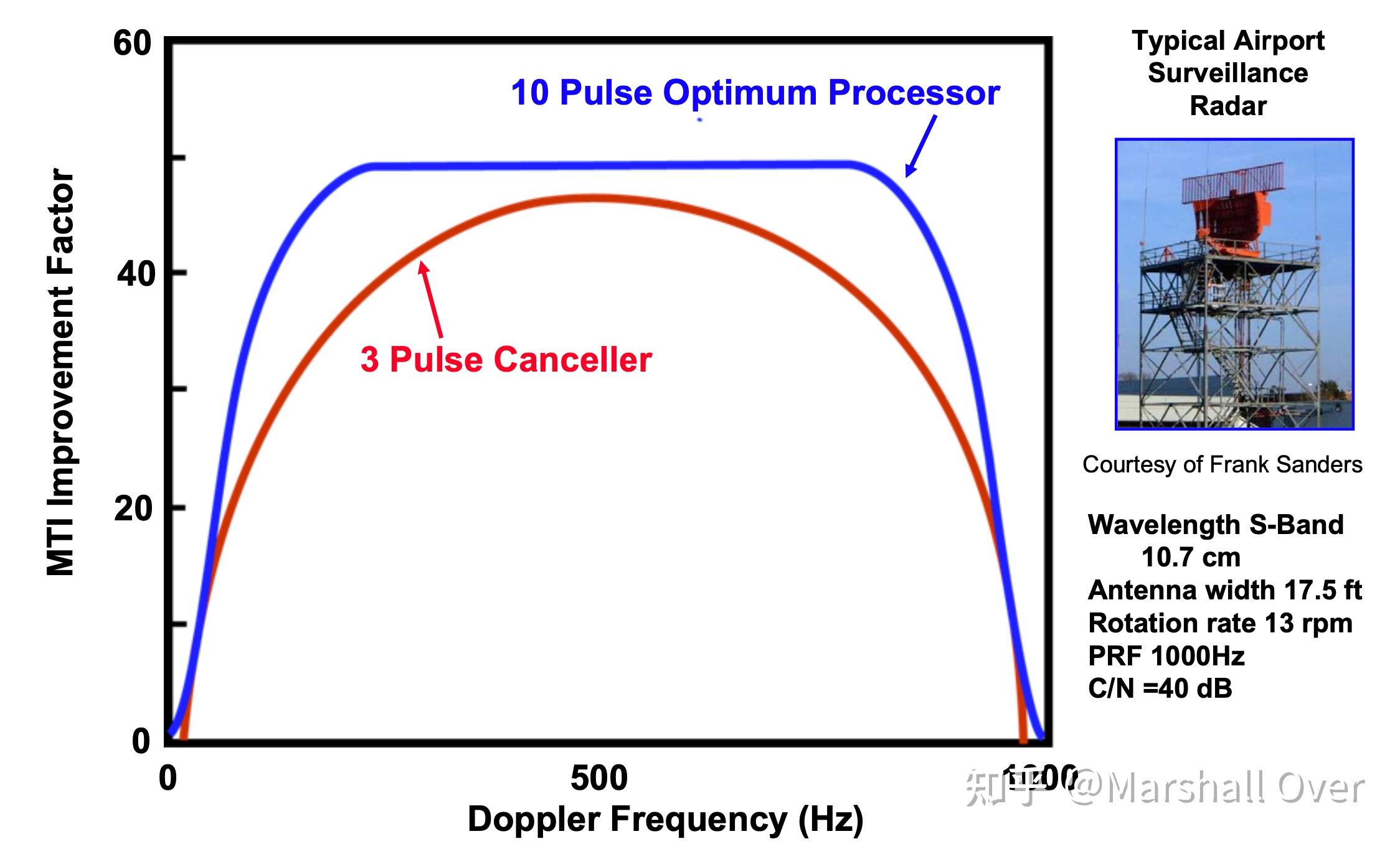
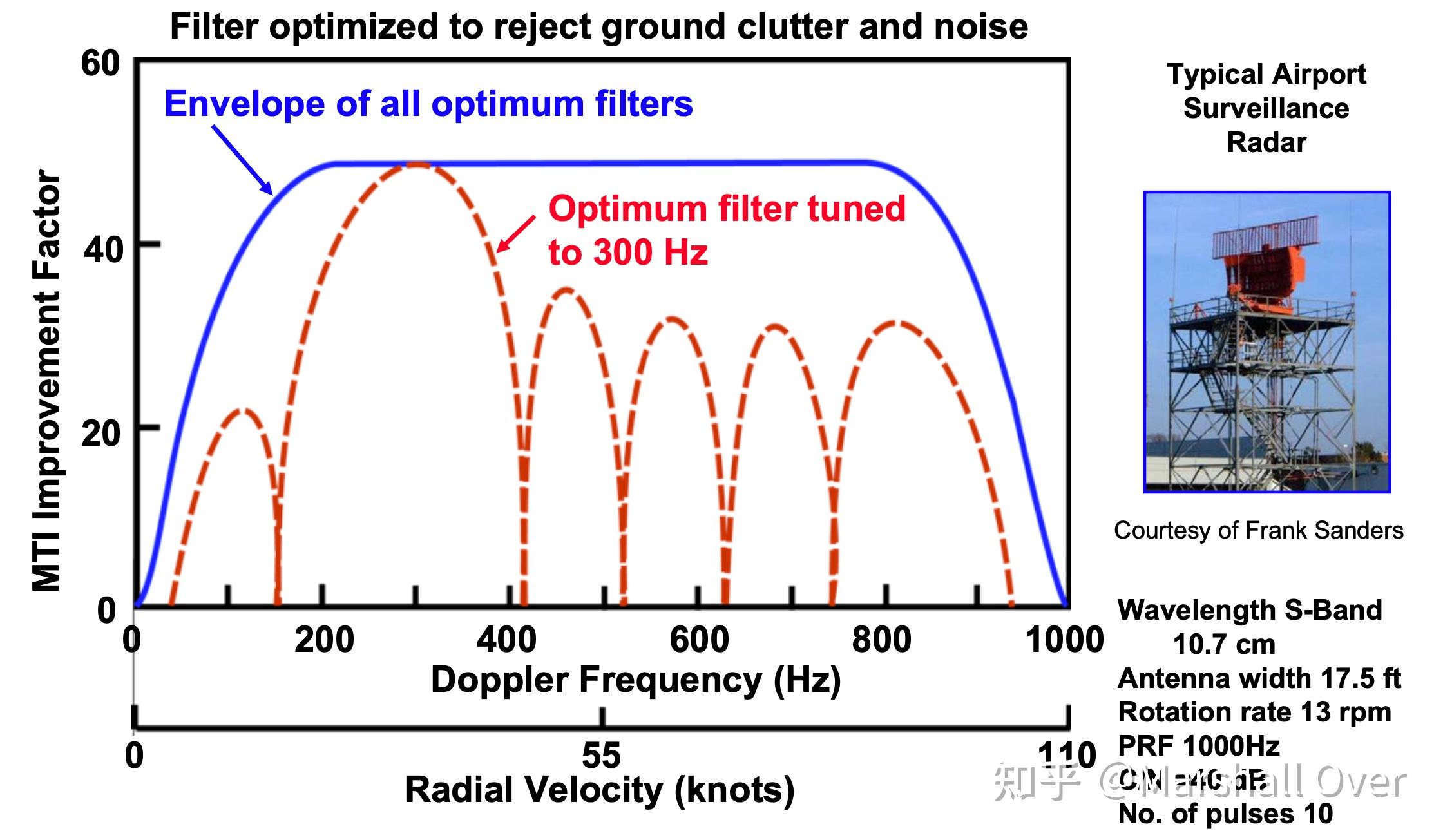
一个最优滤波器的MTI改进：

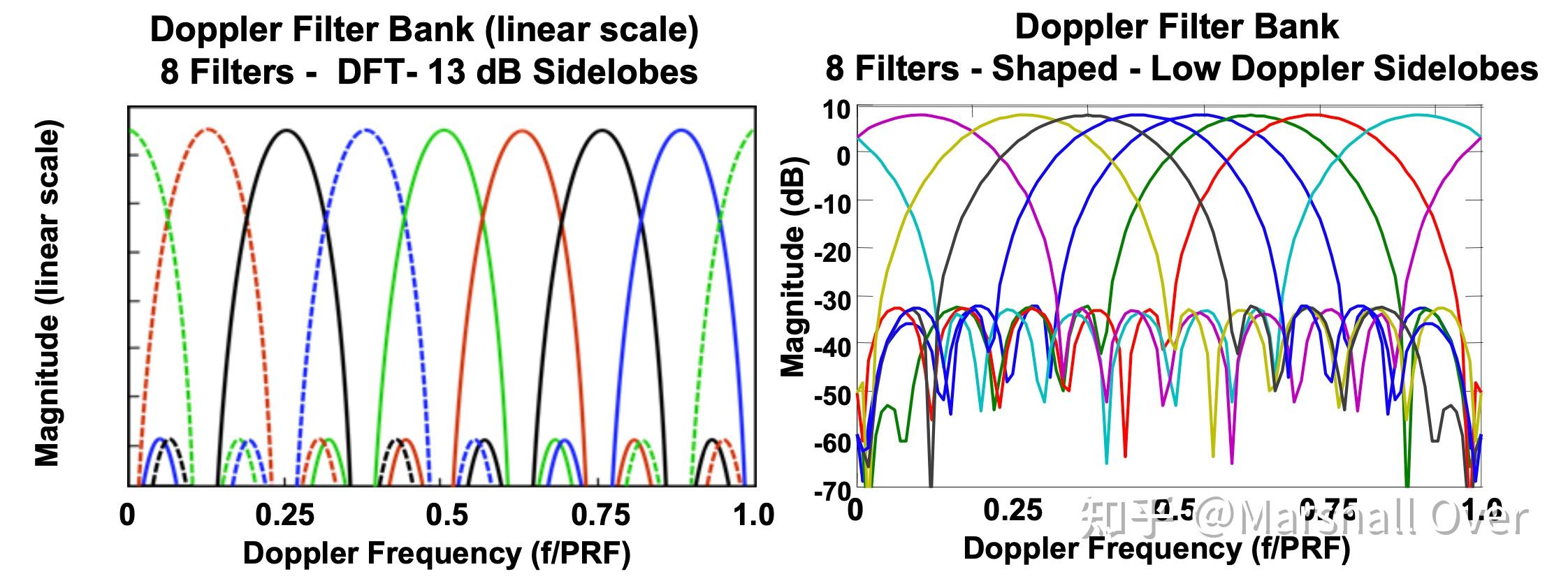
一组多普勒滤波器的实现：实现滤波器组的最简单方法是使用离散傅立叶变换（DFT）；请注意，13dB的旁瓣对雨杂波的抑制效果较差；对输入信号进行加权或使用其他技术（将在下一堂课中讨论），以及对足够数量的脉冲进行积累，即使在大雨中也能提供良好的目标检测结果。

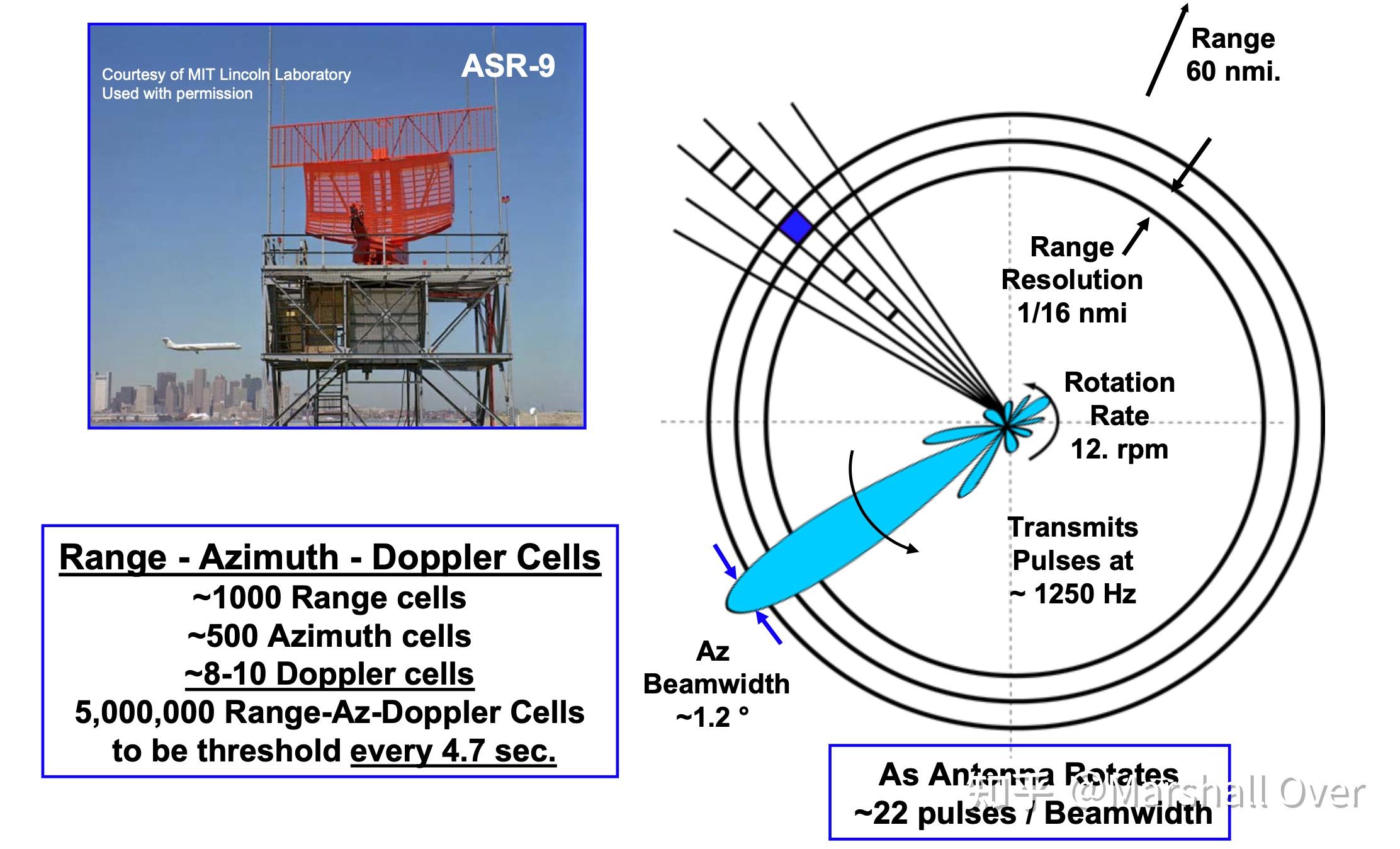
3.2 低重频示例-运动目标检测（MTD）

飞机监视雷达（Aircraft Surveillance Radar，ASR）问题：

运动目标探测器（MTD）处理器：

运动 目标探测器（MTD）：对具有细粒度杂波图的8个或更多脉冲的组进行脉冲多普勒滤波；使用多普勒滤波器组和2个PRF在地面杂波和/或降雨中检测飞机；鸟类和地面交通在后处理中被抑制，使用多普勒速度和第二阶段细粒度杂波图。

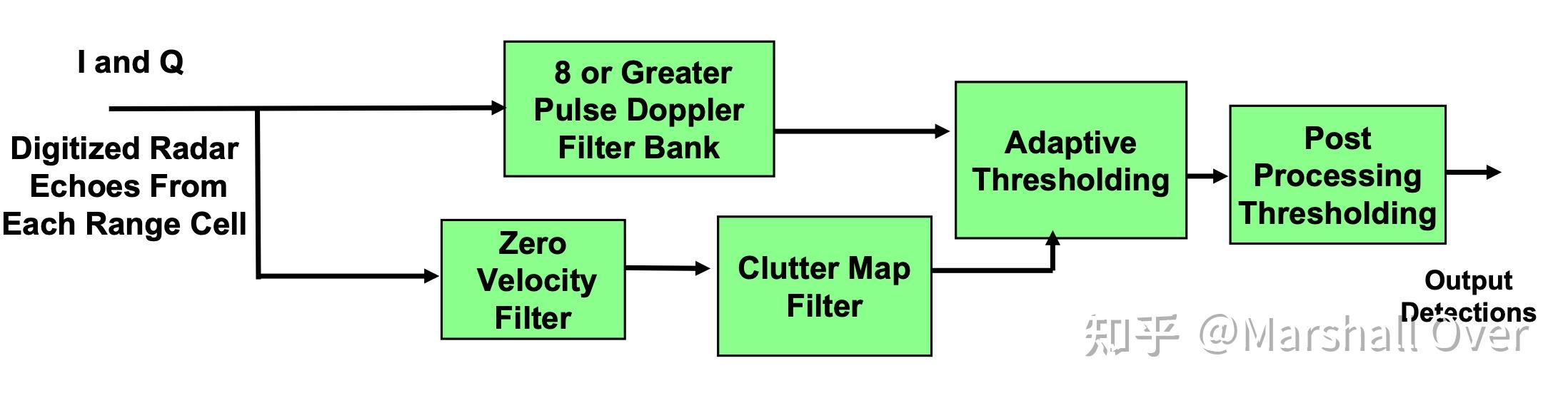
ASR-9 8脉冲滤波器组：

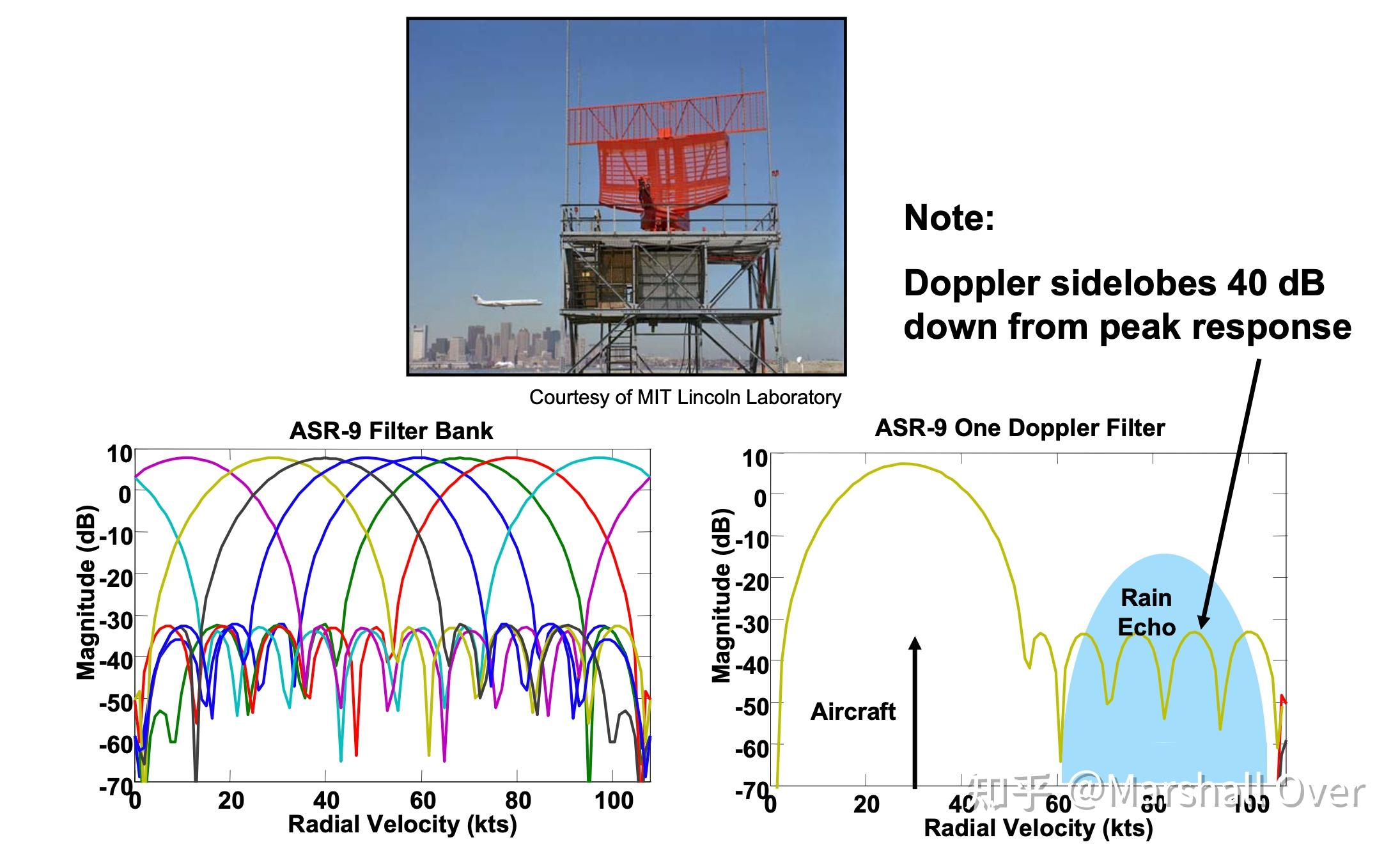
利用两个PRF进行降雨探测：

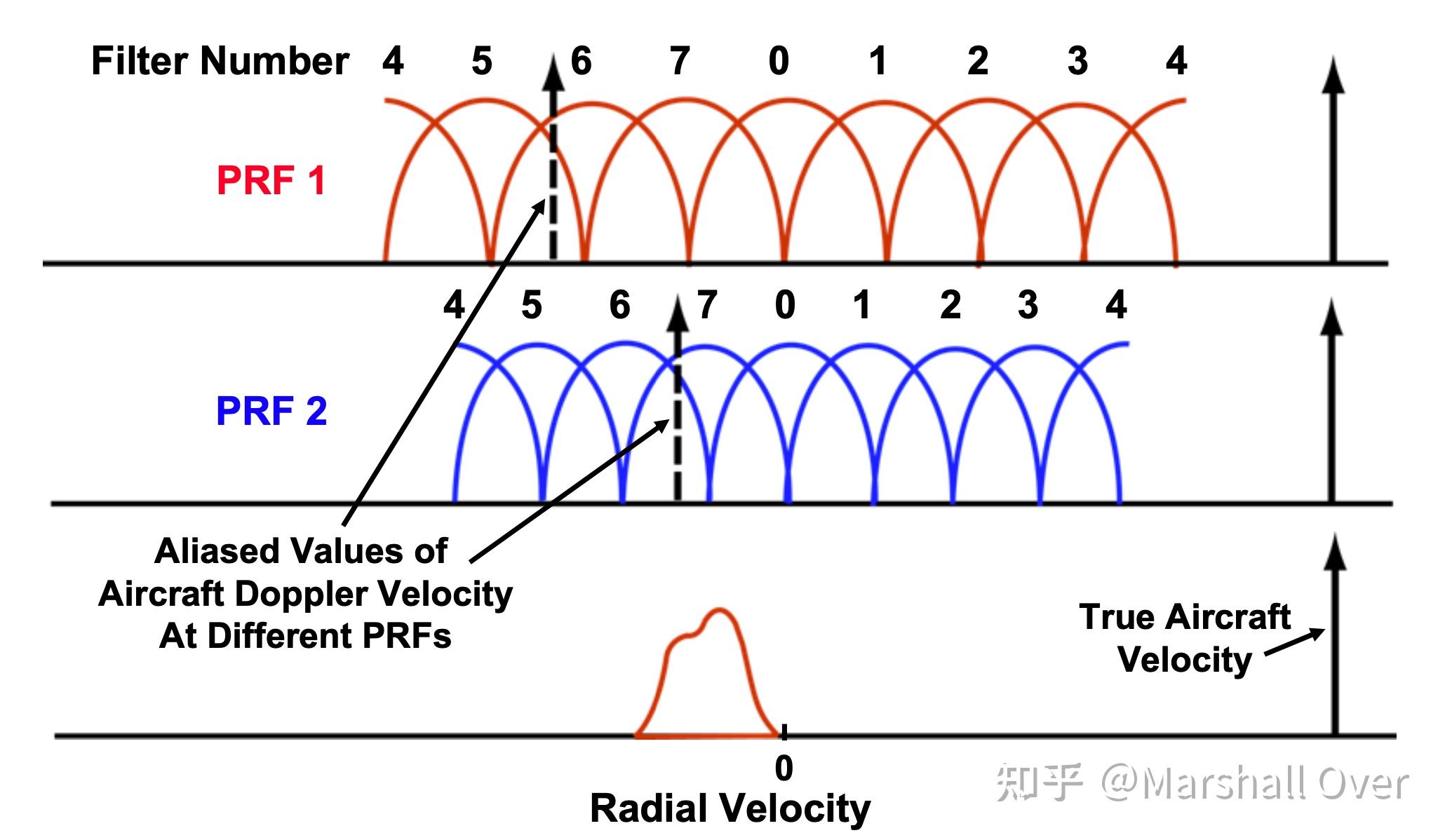
MTD在雨天的表现：

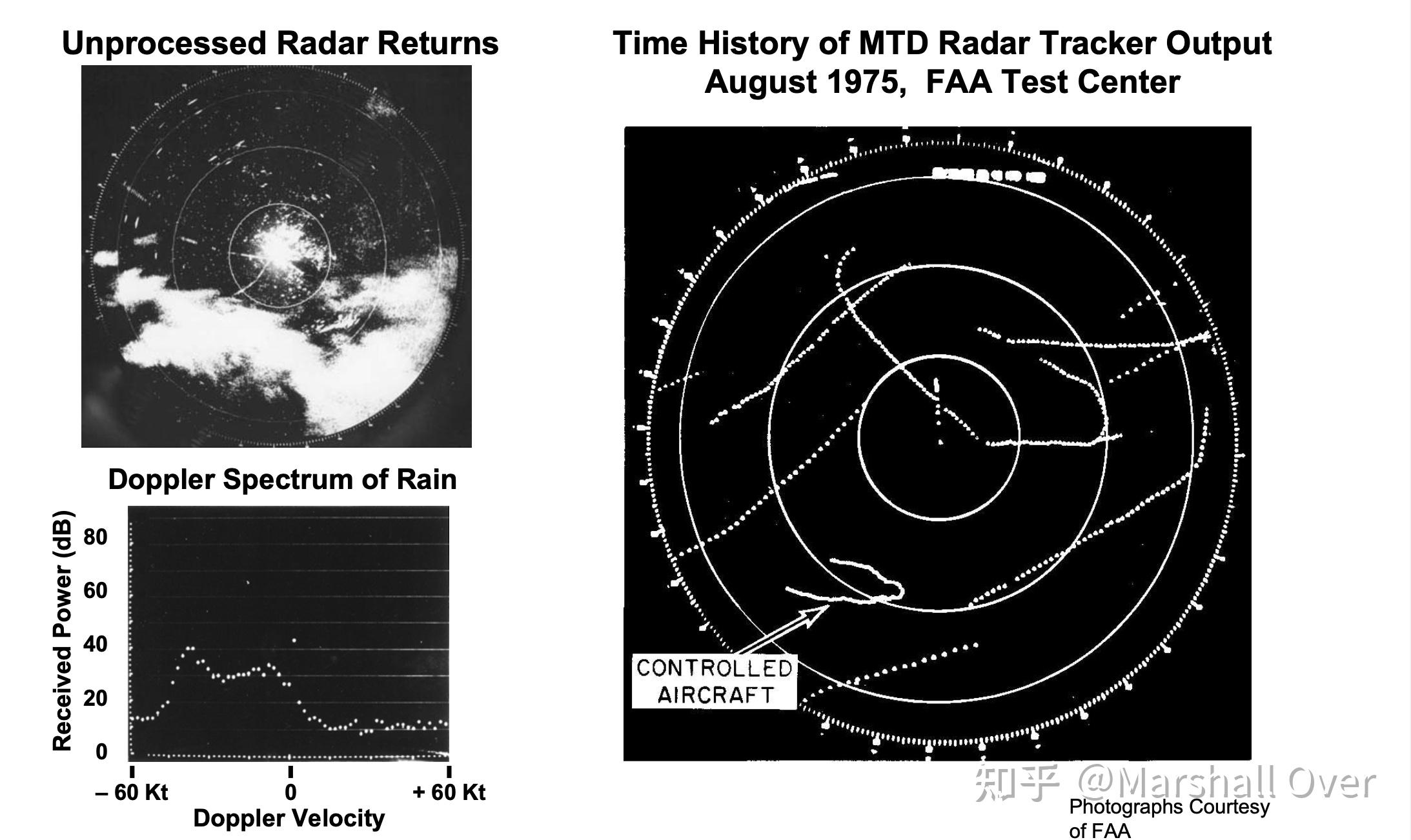
动目标探测器-I（1975）：

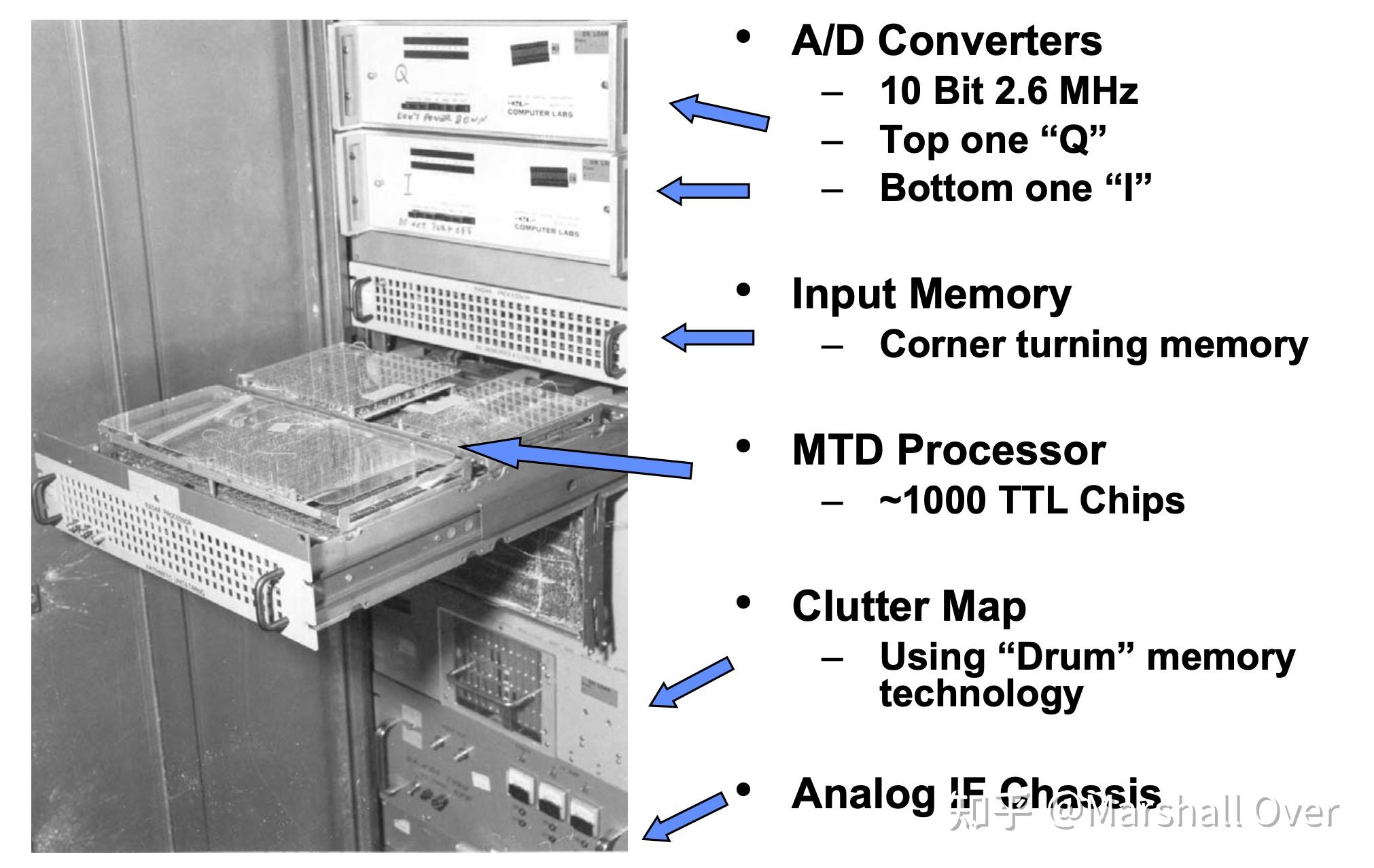
非相干积累与相关杂波的影响：

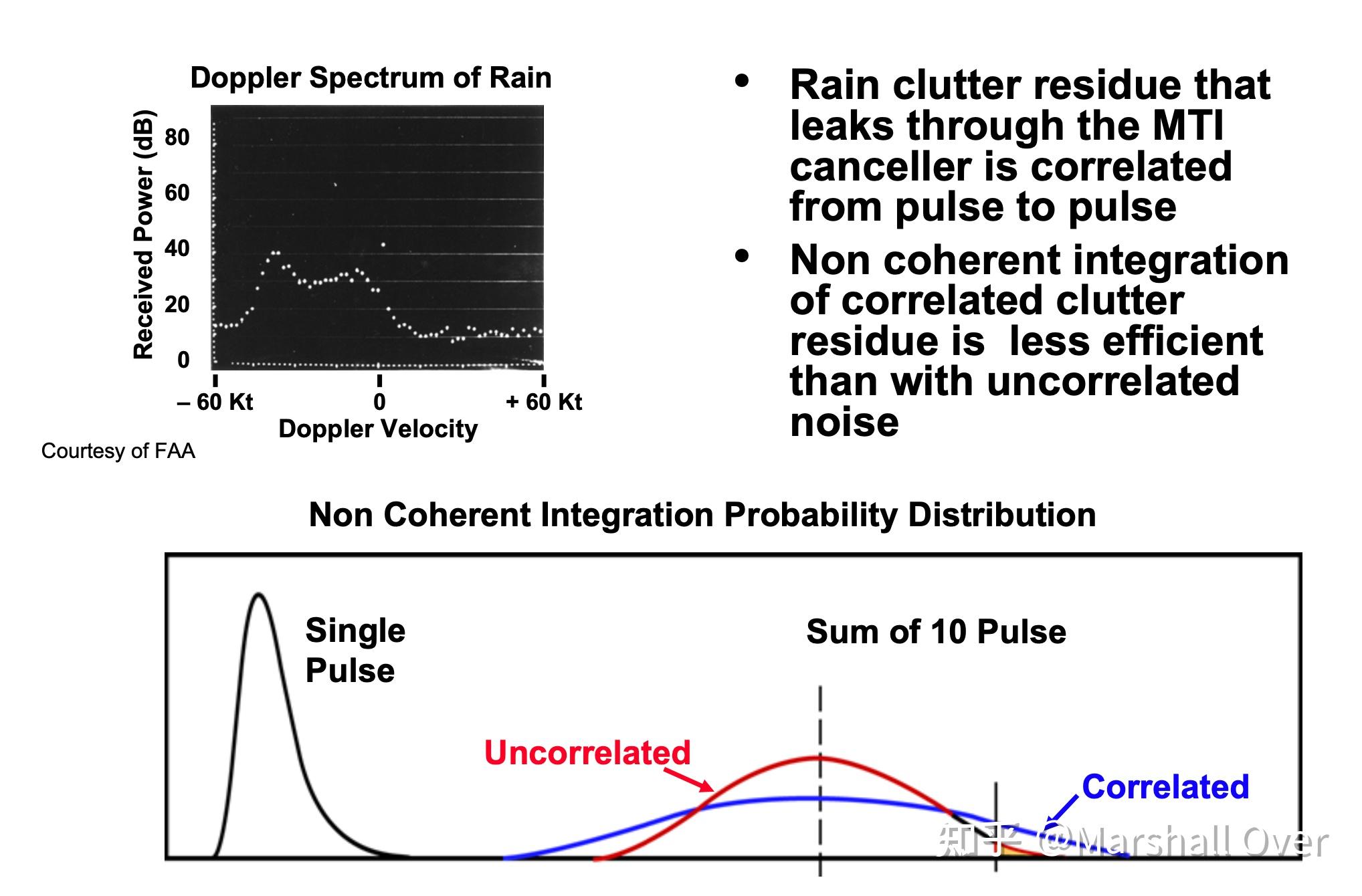
部分相关波形的独立脉冲(Independent Pulses for Partially Correlated Waveforms):部分相关脉冲的非相干积累通常是非常低效的。

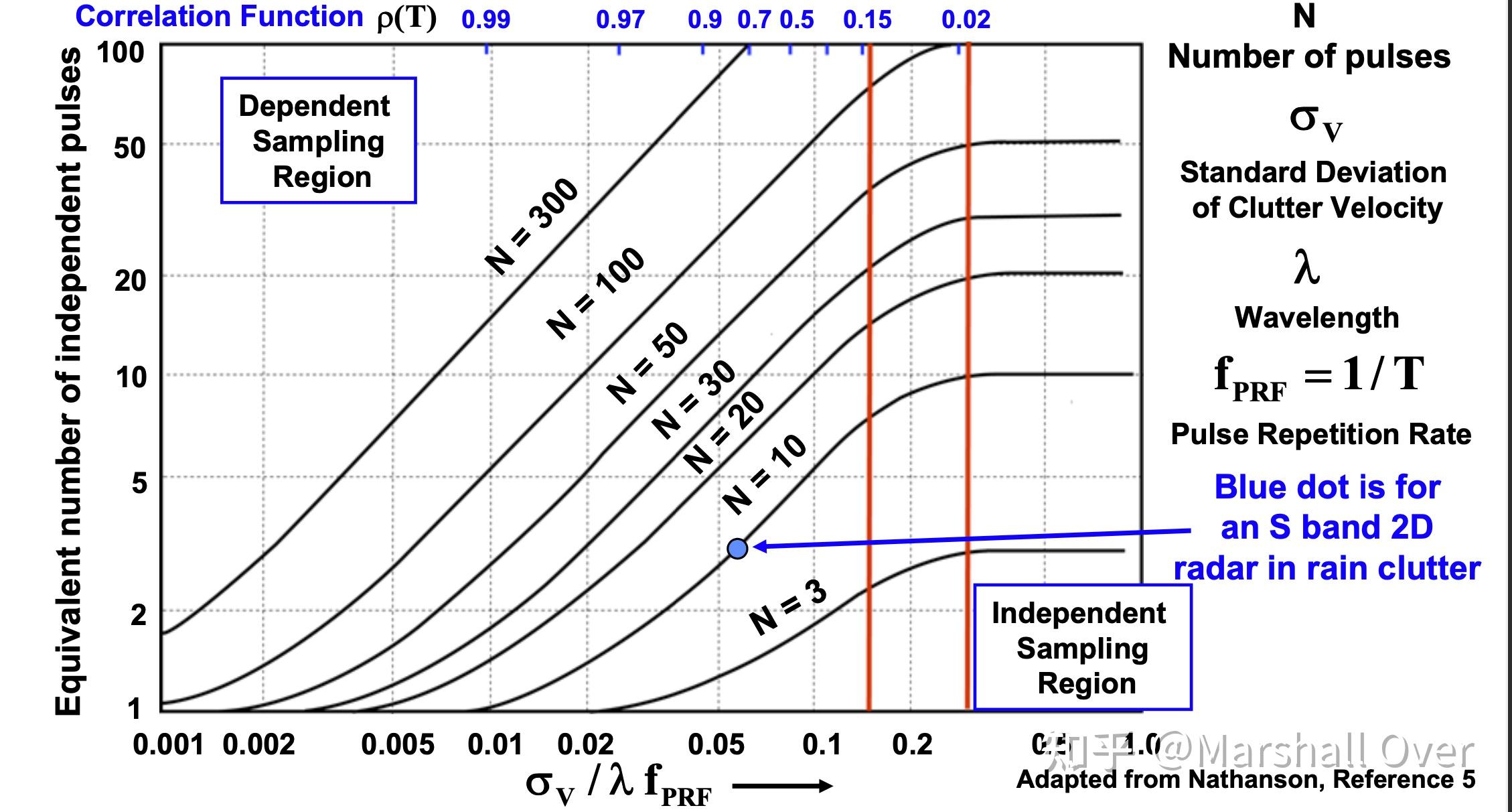
MTD执行（MTD Implementations）：MTD的前两个版本是由麻省理工学院林肯实验室在20世纪70年代初至后期为美国联邦航空管理局设计和建造的，并有大量资料；在对MTD II进行操作测试后，这些概念被纳入了ASR-9的规范中，并与其他改进一起纳入了该雷达；随着数字处理技术和算法技术的进一步改进，这些概念目前几乎在所有地面低重频雷达中都得到了实现，并影响了脉冲多普勒处理在海基和机载平台上的广泛发展。

MTD总结：MTD首次证明，数字信号处理硬件和算法技术可以在几乎所有条件下提供出色的飞机检测，同时抑制所有形式的杂波（地面、雨水等），从而使雷达和信标报告(beacon reports)能够可靠地关联并显示给空中交通管制员。在接下来的几年里，解决这一特定的民用问题一直是将这一通用方法适当应用于许多其他民用和军用雷达问题：

• 理解摩尔定律将允许在不久的将来以成本效益使用处理技术，而今天似乎没有成本效益；
• 集成多个脉冲，使用低多普勒旁瓣来抑制移动杂波（雨、箔条、海杂波等）；
• 使用高分辨率杂波图检测切向目标；
• 综合解决“信号处理到雷达目标显示”问题。

MTD杂波图技术：杂波图是一种存储器，用于存储雷达覆盖范围内每个距离CPI单元的噪声和杂波回波值。杂波图通常使用递归滤波器来实现；对于每个范围CPI单元，杂波图使用以下算法：

A(n+1)=\frac{1}{N}(A(n))+(1-\frac{1}{N})(A(n-1))\tag{1}

其中N=8为MTD脉冲数，n为扫描号。

它们用于检测径向速度接近零且后向散射回波大于杂波图中存储的杂波和/或噪声振幅的目标；杂波图通道提供了一种检测多普勒滤波组子集未检测到的目标的方法，这些目标与零多普勒相邻，其形状设计为增强抑制零多普勒附近的地面回波。

杂波图门限：

杂波图后信号处理技术：

3.3 距离-多普勒模糊

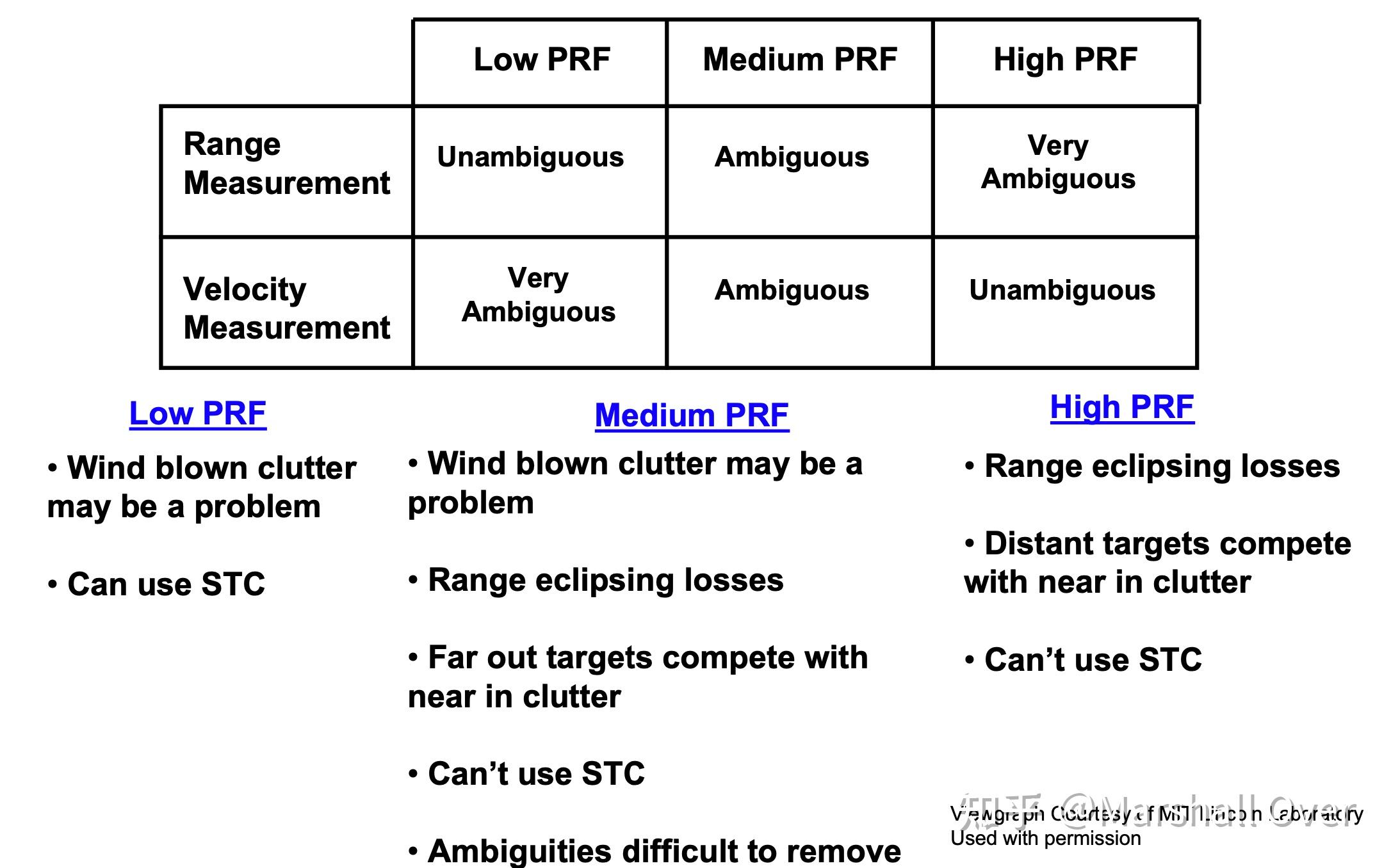
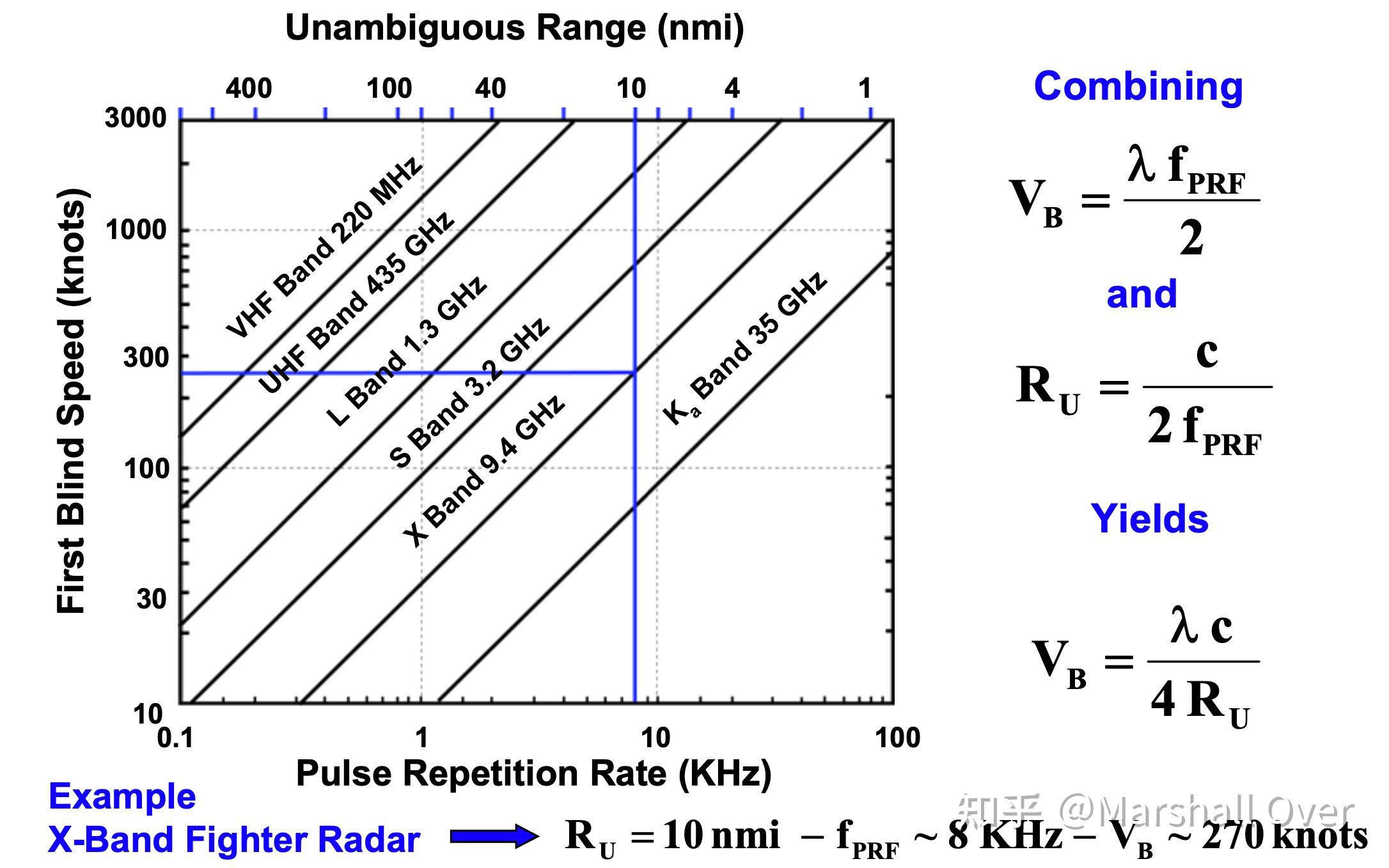
无模糊距离和速度范围：

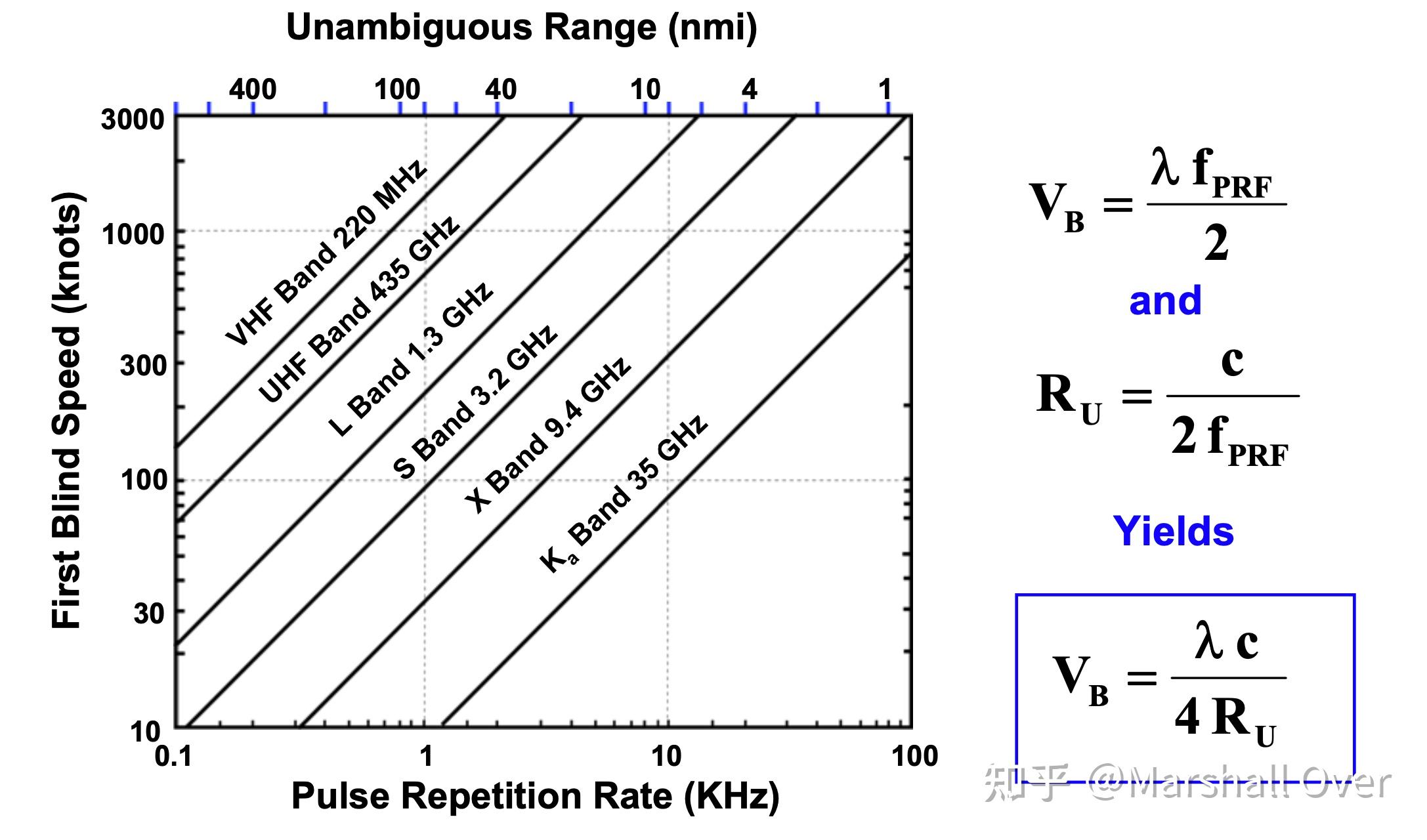
时间灵敏度控制：

MTI和脉冲多普勒雷达的分类：

3.4 模糊分辨率-中国余数定理

速度模糊解决方案：将停留时间拆分为不同PRF下的多个CPI；扫描到扫描，甚至脉冲到脉冲的变化也是可能的；移动盲速度以确保检测到所有非零速度目标；真正的目标速度是CPI之间出现最佳相关性的地方；选择PRF，以便在上面出现最小公倍数。

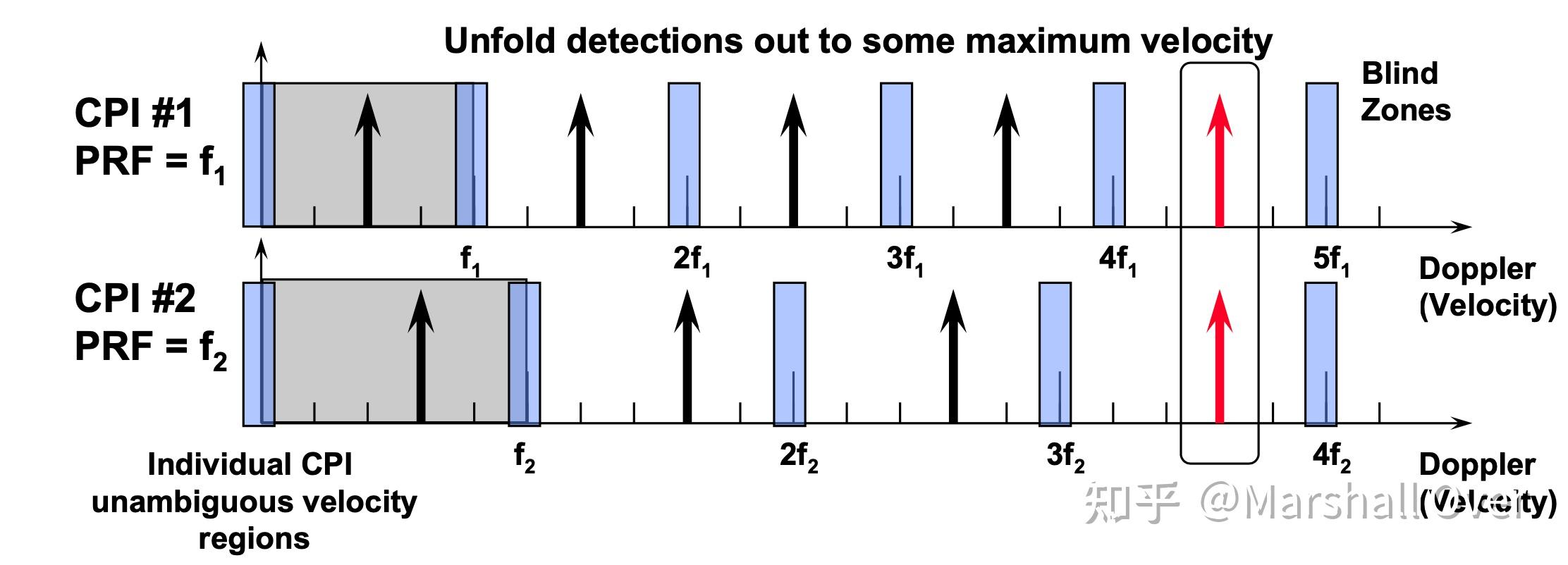
Chinese Remainder Theorem：

Example - Chinese Remainder Theorem：

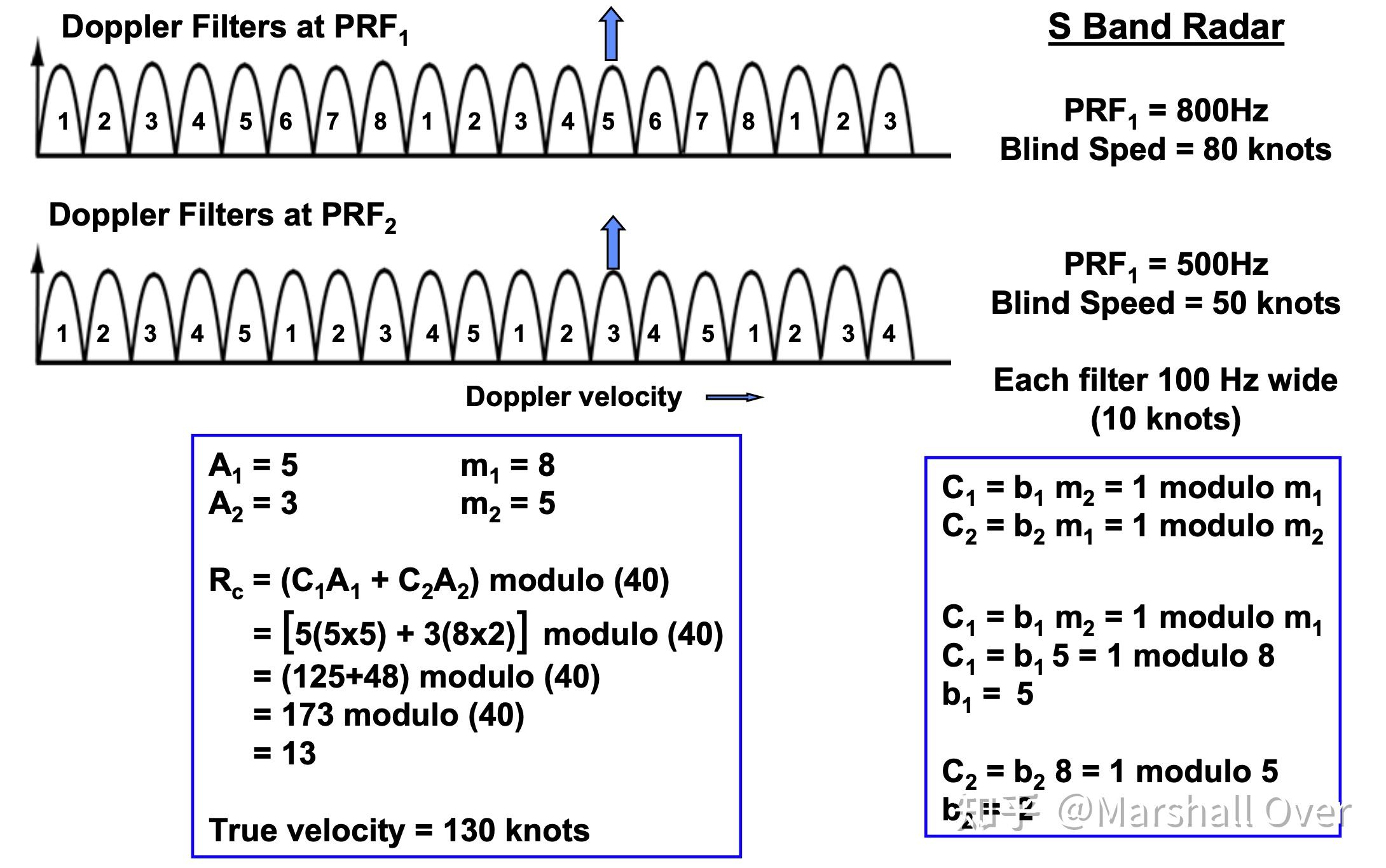
Example - Chinese Remainder Theorem：

3.5 模糊函数

匹配滤波回顾：

模糊函数：模糊函数是发射信号和接收到的多普勒频移回波的互相关（匹配滤波器的输出）的平方幅度。

模糊函数性质：

模糊函数三种形式：

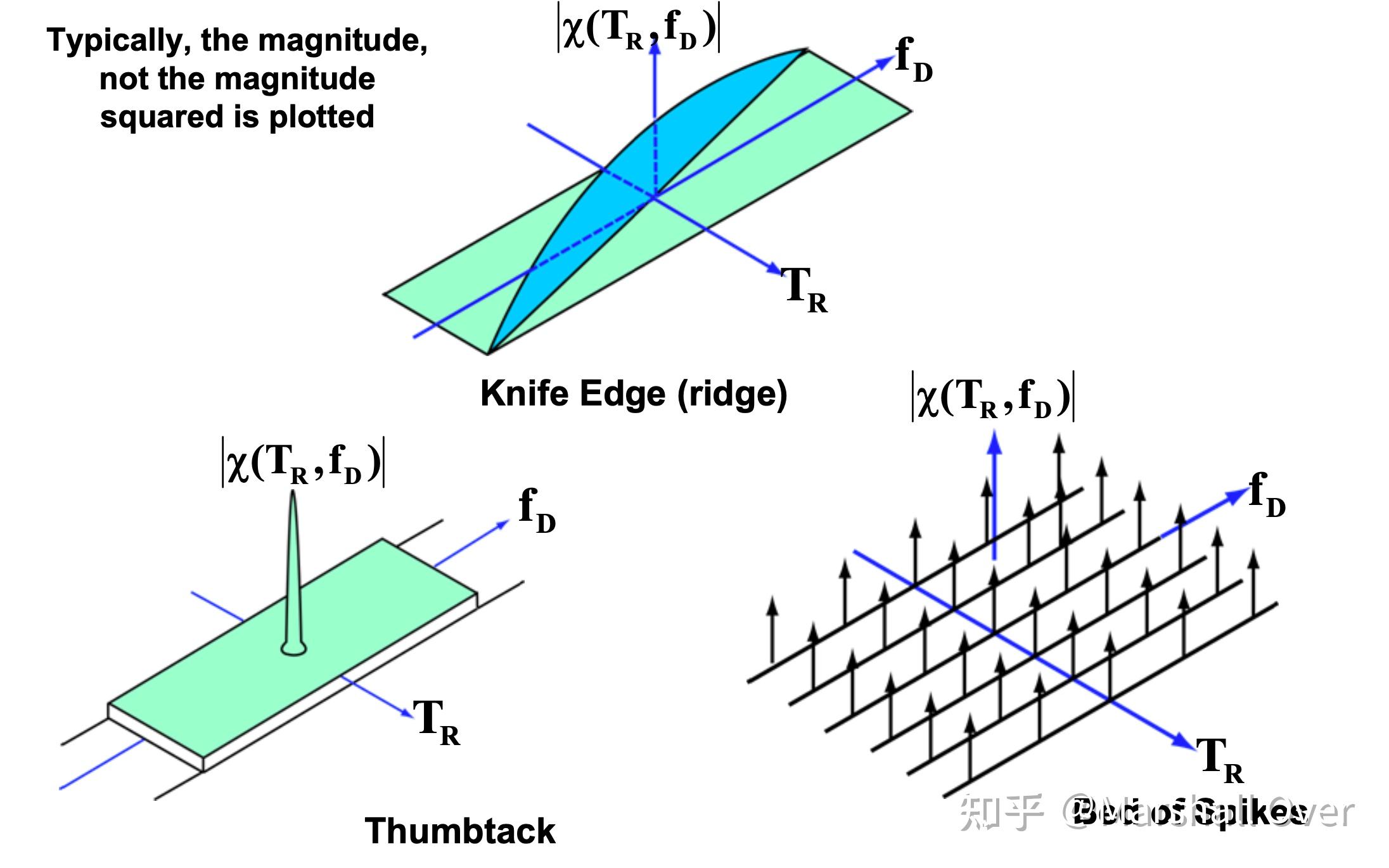
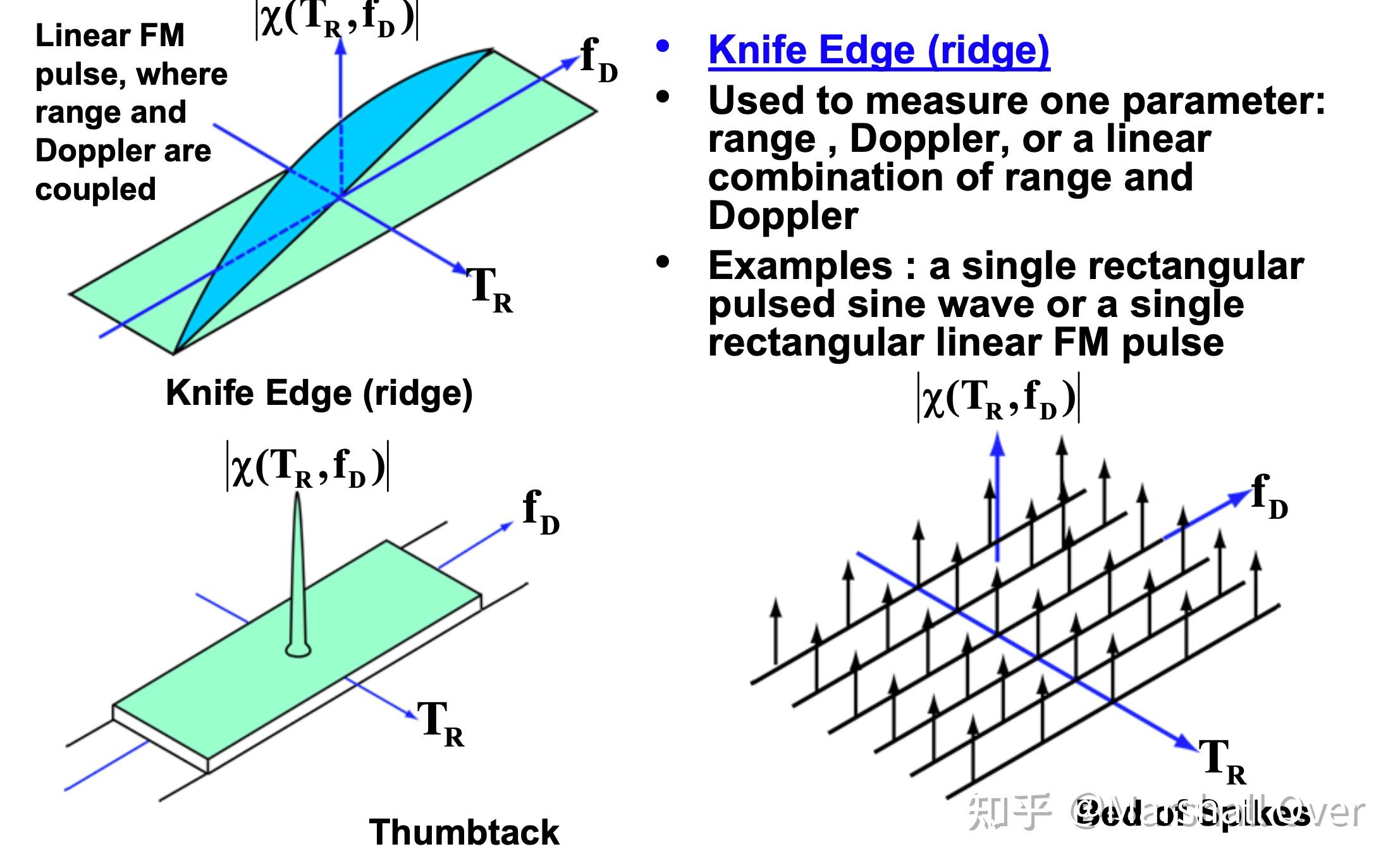
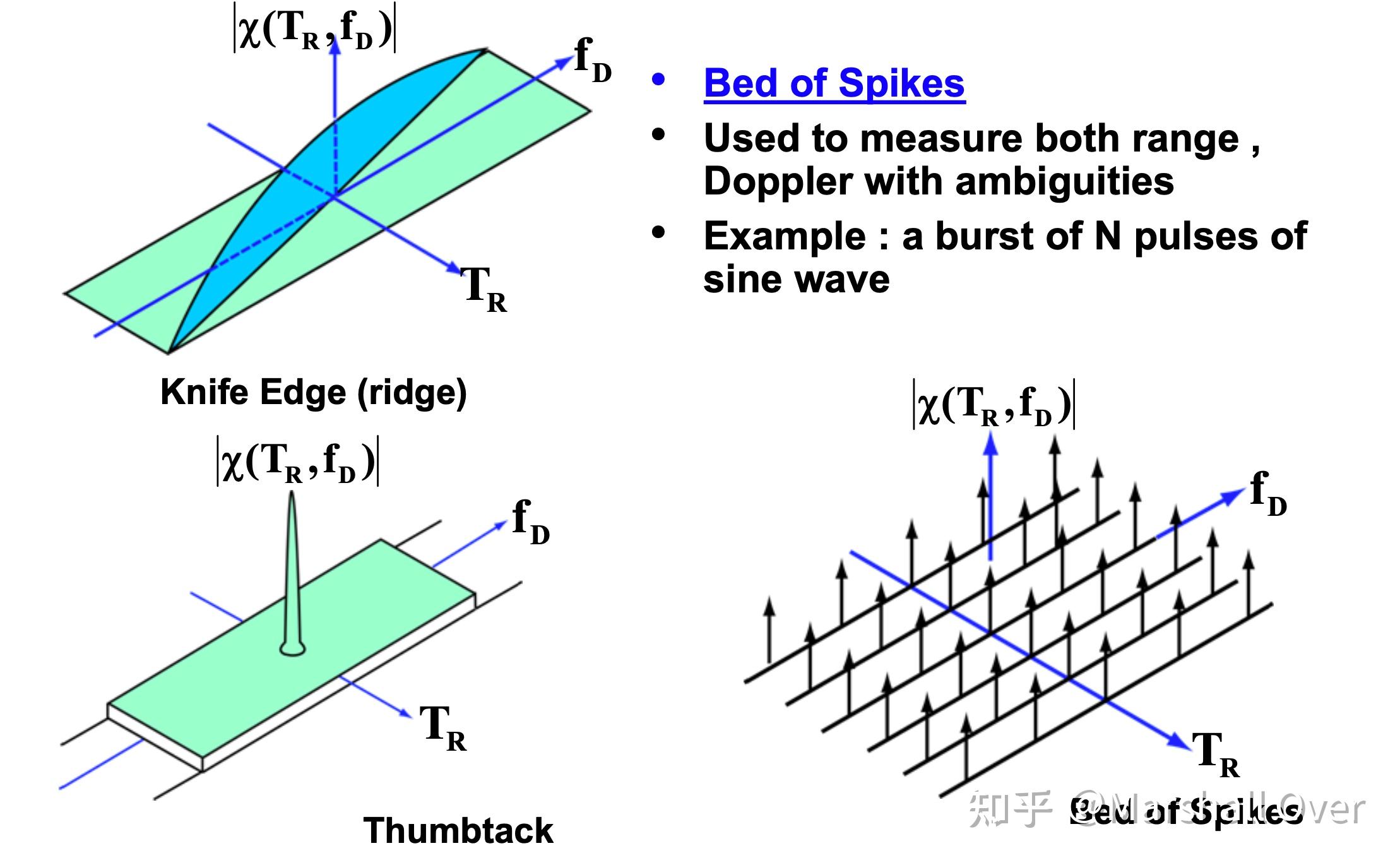
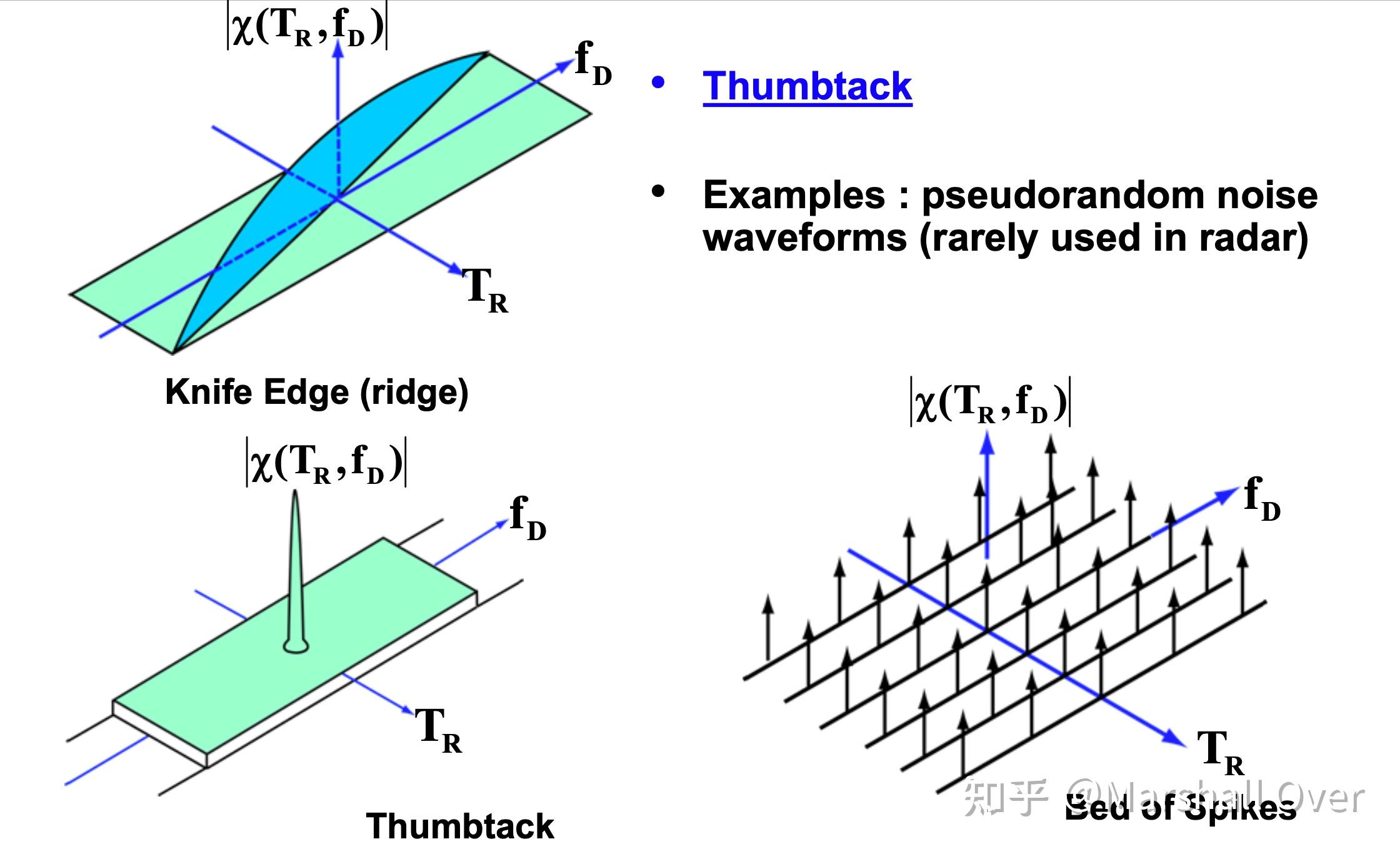
方波的模糊函数：

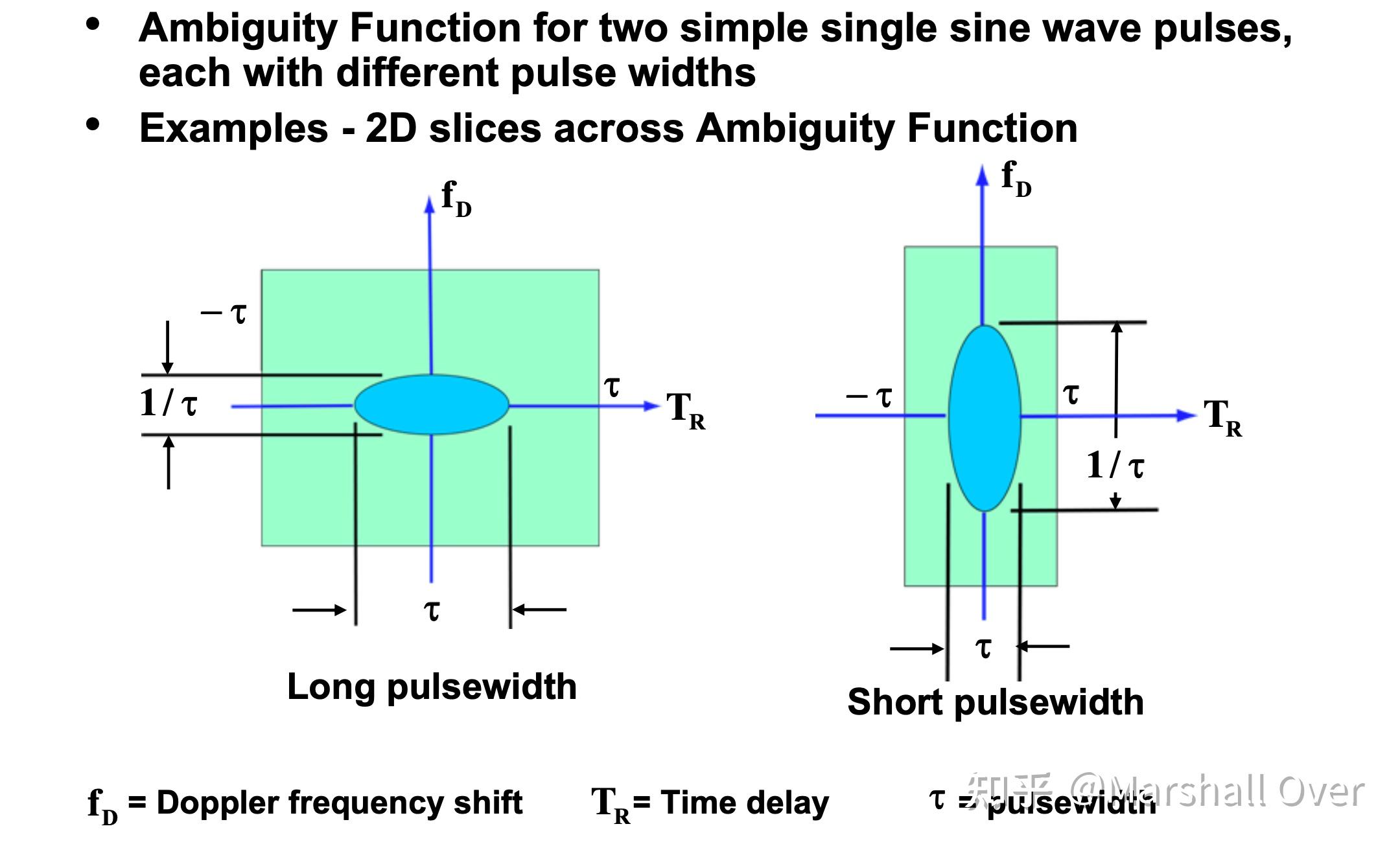
Ambiguity Function of Rectangular Pulse：

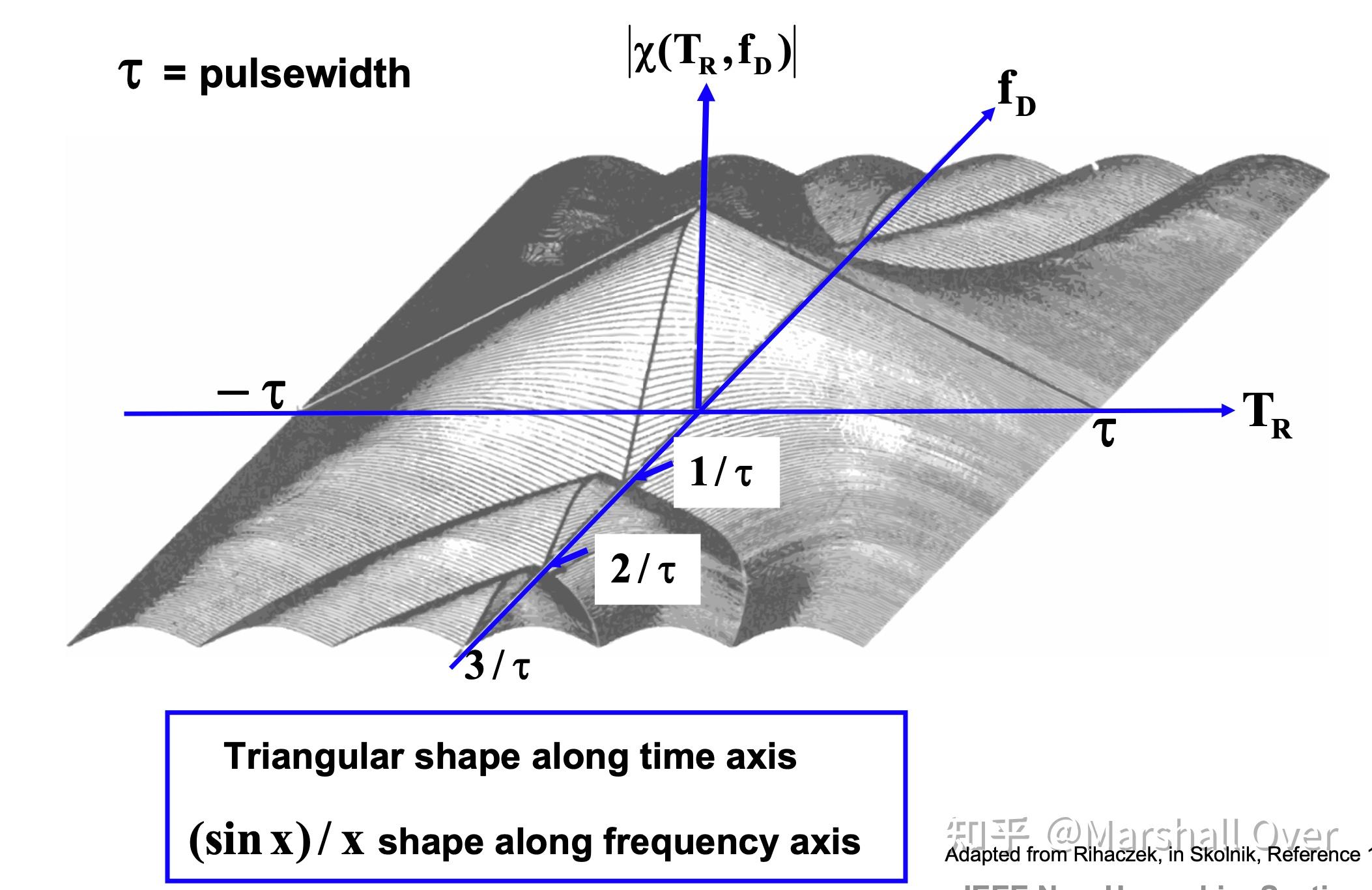
Ambiguity Function of Linear FM Pulse：

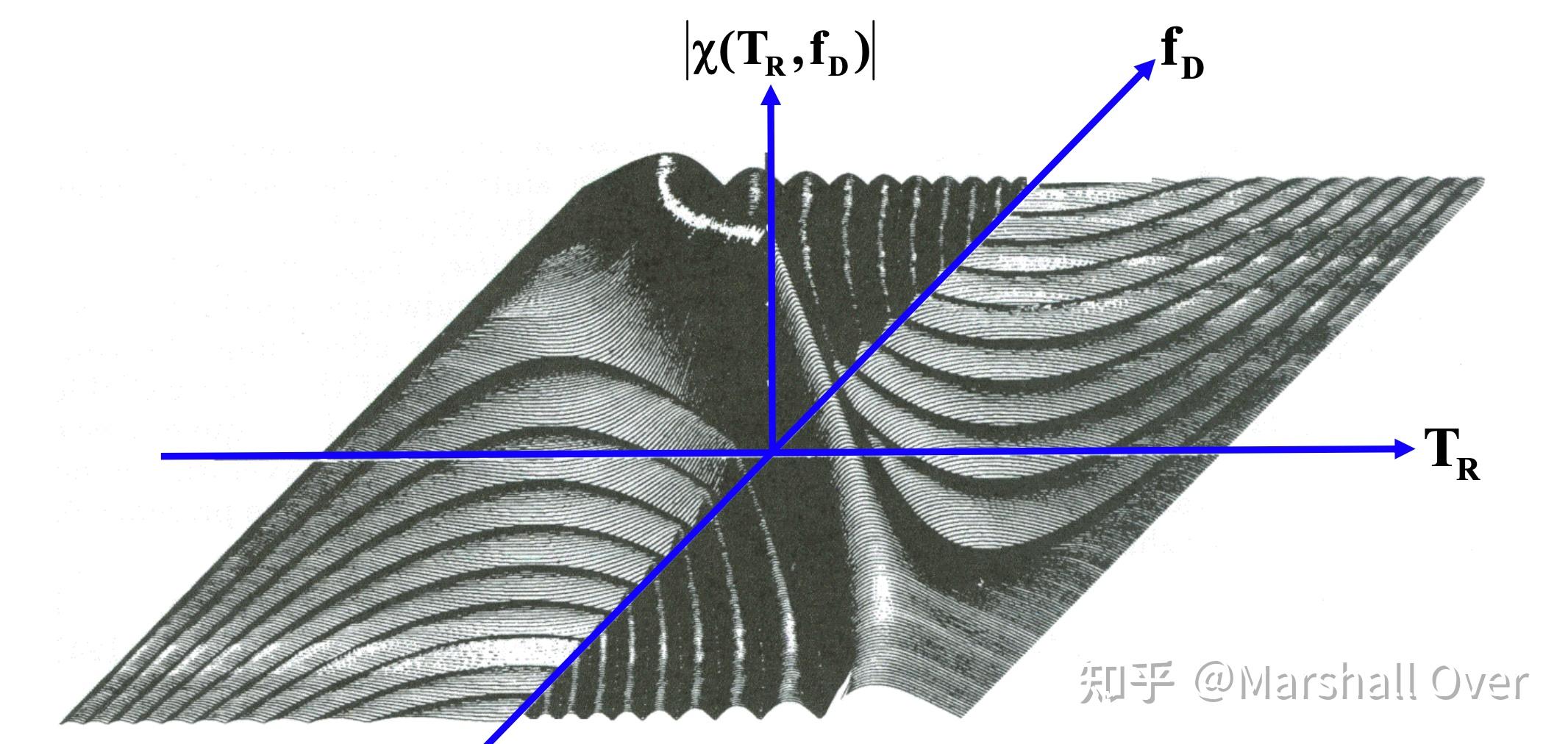
Ambiguity Function of Linear FM Pulse：

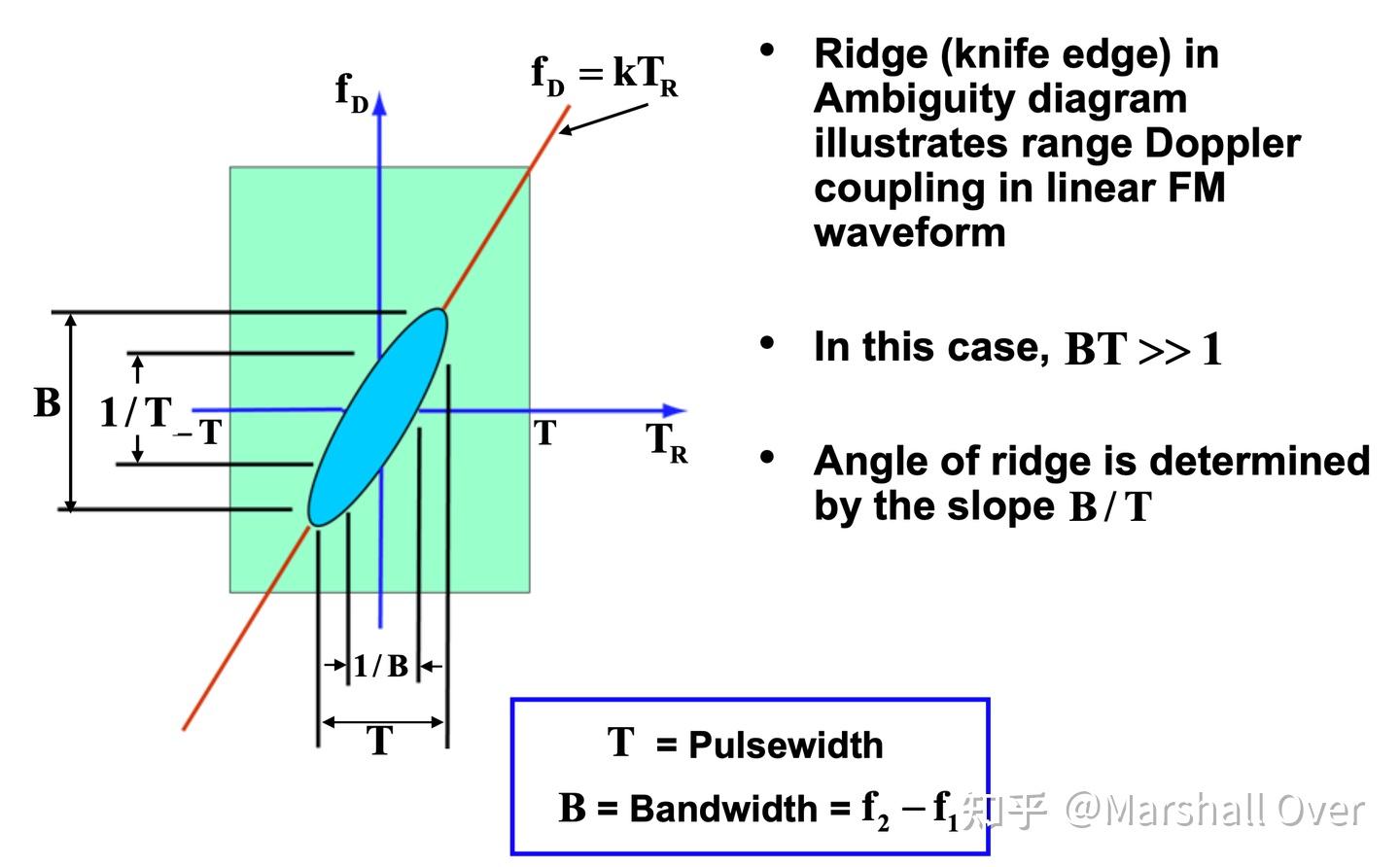
Ambiguity Function for a Burst of Five Rectangular Pulses：

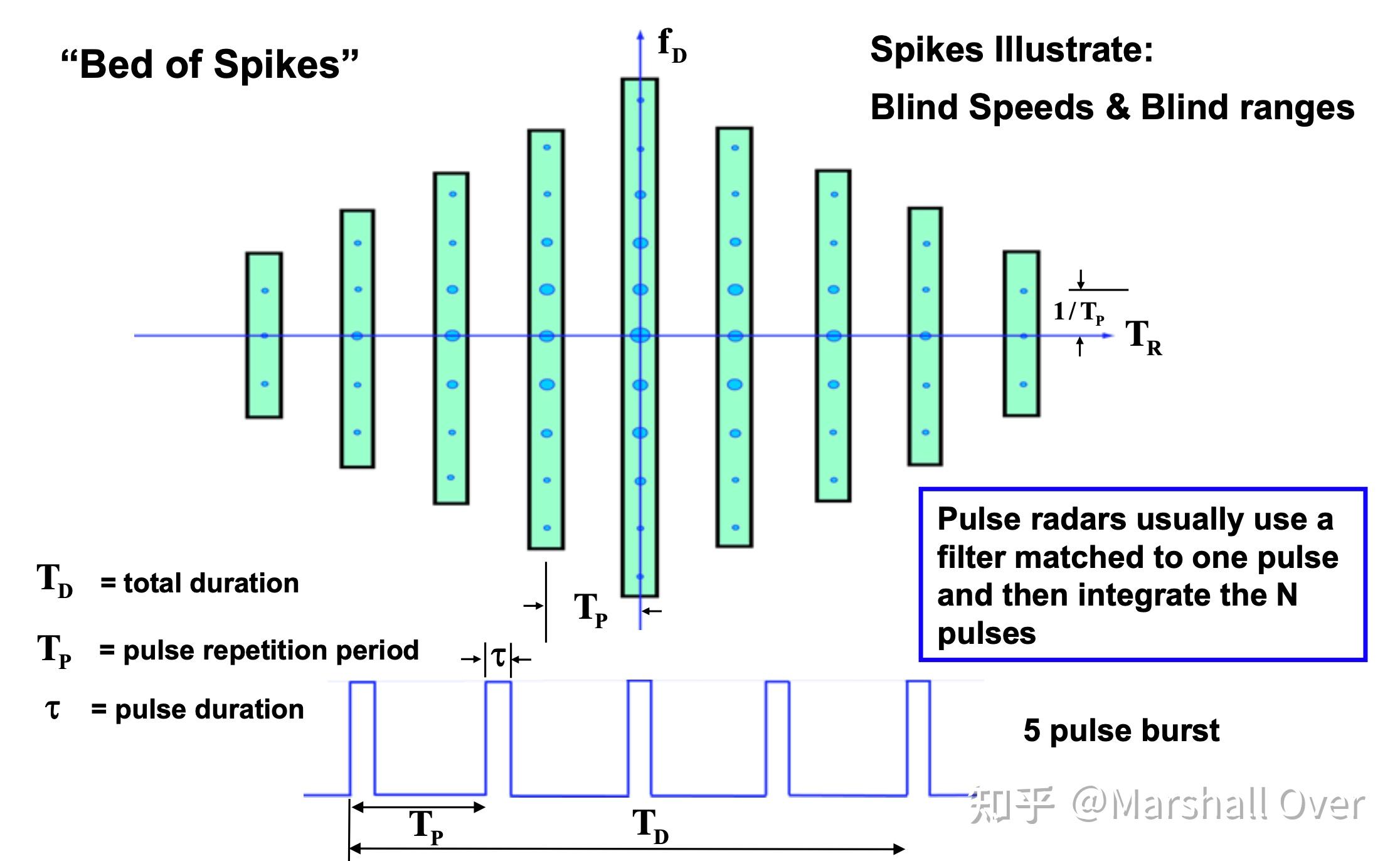
Ambiguity Diagram for Phase Coded Pulse：

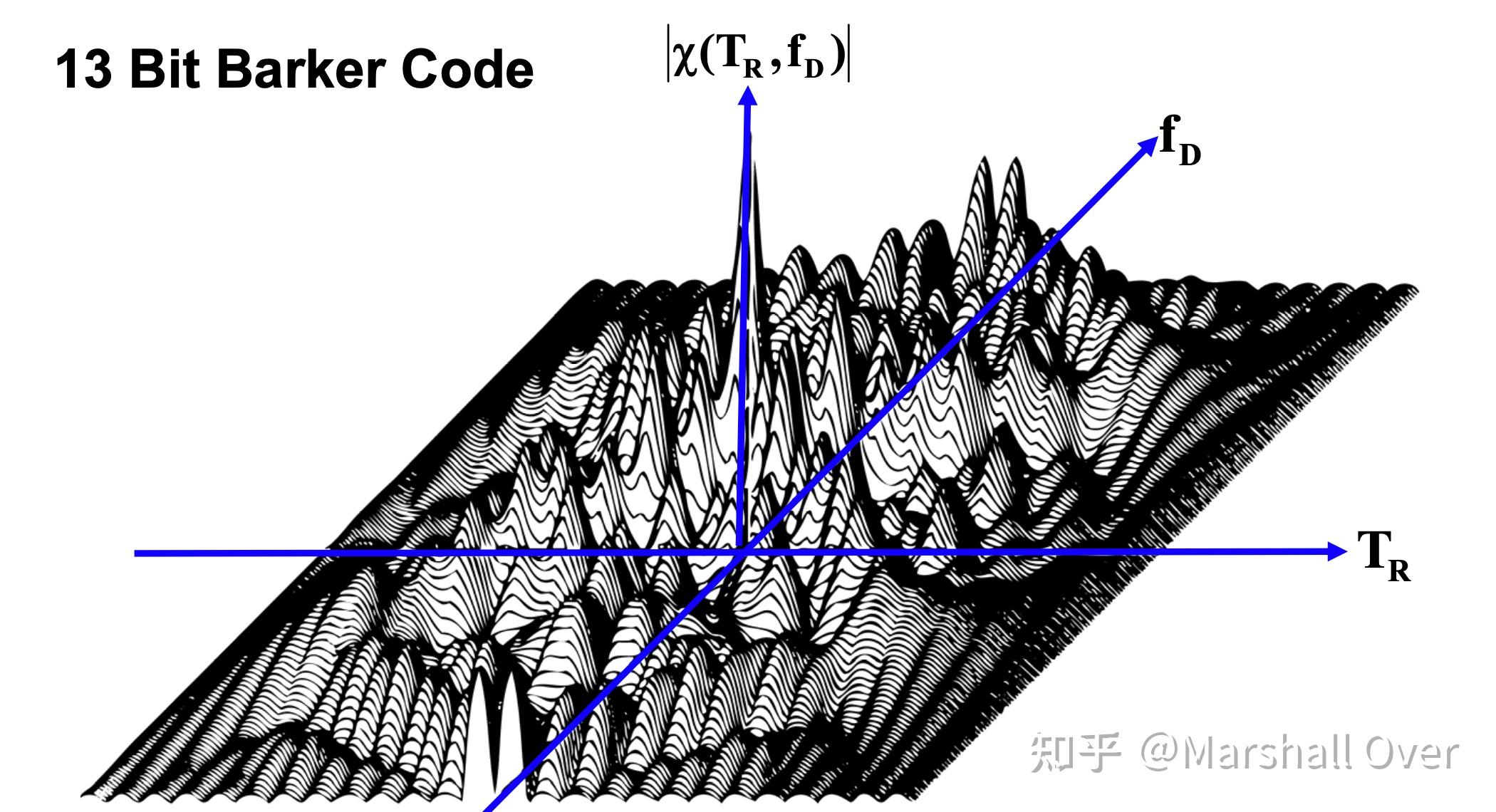
3.6 机载脉冲多普勒问题回顾

机载平台上的脉冲多普勒雷达技术：

多普勒速度-距离模糊问题：

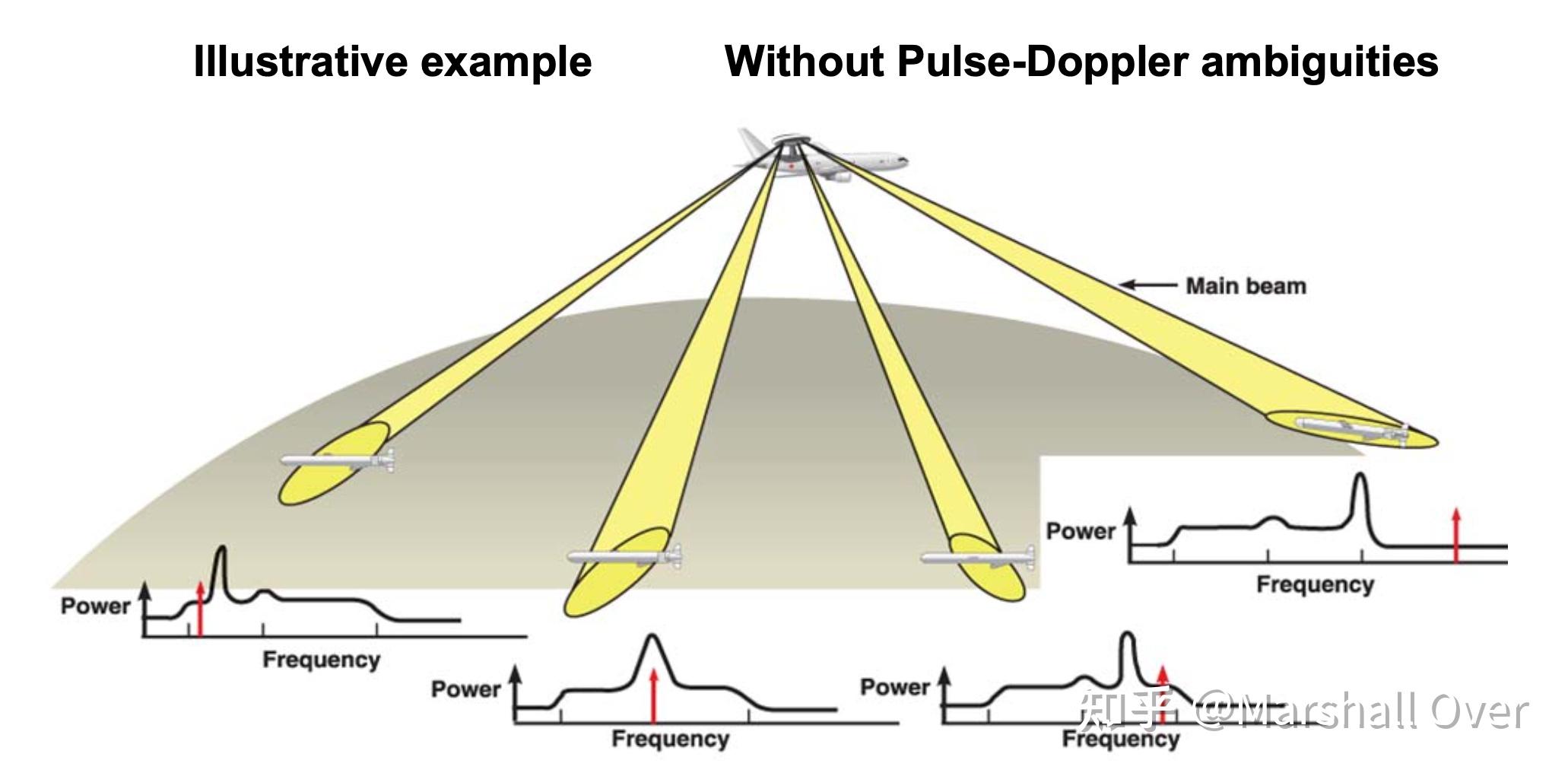
机载雷达杂波特性：主波束杂波的多普勒频率取决于扫描方向；目标的多普勒频率取决于扫描方向和方位角。

4 总结讨论

• 脉冲多普勒技术可用于以最佳方式抑制各种形式的雷达杂波；
• 运动目标检测器是在低重频雷达中实现的接近最佳多普勒处理和相关自适应阈值技术的一个例子；
• 距离和多普勒速度的模糊性可以通过发射具有不同PRF的多个脉冲串来解决：中国余数定理是解决这些歧义的有用工具
• 模糊函数是理解不同波形的时间和频率性质的有力工具。

5 参考文献

[1] 百度翻译

[2] MIT 公开课： Radar Systems Engineering