博弈论总结

标签：总结石子 xor 游戏博弈论必胜 SG 节点

博弈论题目解题的关键在于找到一个状态a，设它的否定为状态b，状态a满足：不论怎么操作对手的状态a一定会转化为状态b和一定存在一种从状态b转化到状态a的操作。满足这样两条性质的状态a为必败态，b为必胜态。想求SG，需要对后续节点实行mex函数，想求是否为必胜必败态，需要求异或和如果使用SG来做，不需要分析什么，直接对所有子游戏求异或和最后判断与0的关系即可(对应Nim游戏的推广)；如果不使用SG，那么就需要分析出必败态和必胜态，(对应Nim游戏)

Nim游戏

给定n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。问如果两人都采用最优策略，先手是否必胜。

Nim定理

假设各堆石子数量为$A_1, A_2, ..., A_n$，那么先手必胜的充分必要条件为 $A_1 \ xor \ A_2 \ xor \ ... \ xor \ A_n \ \neq \ 0$

定理证明

前提说明 为何本题使用异或进行判断不是我们能想到的，那是数学家的工作，我们能做的就是理解相关定理的证明并记忆相关题目的特征。首先必须明确一个必败局面是**$A_1 \ xor \ A_2 \ xor \ ... \ xor \ A_n \ = \ 0$，该结论在《算法竞赛进阶指南》中并没有给出详细说明，书中的说法是当所有石子数量均为0时是先手必败局面，此时$A_1 \ xor \ A_2 \ xor \ ... \ xor \ A_n \ = \ 0$，但是这只是一种特殊情况，并非一般情况，所以这里我也不太清楚，不过由于后续证明必须用到这个结论，所以这里只能先暂时这么认定。证明若想要证明异或和不为0是先手必胜的条件，也就是证明异或和不为0的状态x是一个必胜态，需要从以下两个角度进行证明一、通过某些操作可以使得状态x到达必败态，当先手处于必胜局面时，必须保证对手面对的一定是必败局面，即通过某个**操作可以使得任意一个必胜局面转化为必败局面

对于任意一个局面，如果$A_1 \ xor \ A_2 \ xor \ ... \ xor \ A_n \ = \ x \ \neq \ 0$，设x的二进制表示下最高位的1在第$k$位，那么至少存在一个$A_i$，它的$k$位是1，因为$x \ xor \ x = 0$，所以我们只需要从$A_i$中拿走$A_i - (A_i \ xor \ x)$，使得$A_i$变为$A_i xor x$，从而得到$A_1 \ xor \ A_2 \ xor \ (A_i \ xor \ x) \ ... \ xor \ A_n \ = A_1 \ xor \ A_2 \ xor \ ... \ xor \ A_n \ = \ x \ xor \ x \ = \ 0$的必败局面

二、不论采取什么操作必败态一定会转化为状态x，，当对手处于必败局面时，必须保证先手面对的一定是必胜局面，即通过任何操作可以使得任意一个必败局面转化为必胜局面

对于任意一个局面，如果$A_1 \ xor \ A_2 \ xor \ A_i \ ... \ xor \ A_n \ = \ 0$(1式)，那么无论如何取石子，都可以得到所有石子数量异或和不为0的局面，即必胜局面。采用反证法，假设从$A_i$中取出一些石子后数量变为$A_i^{'}$，且$A_1 \ xor \ A_2 \ xor \ A_i^{'} \ ... \ xor \ A_n \ = \ 0$(2式)，将1式和2式左右两侧分别进行异或，结果为$A_i \ xor \ A_i^{'} \ = \ 0$,即$A_i \ = \ A_i^{'}$,这显然和假设是矛盾的，所以对于一个必败局面，无论从哪堆石子中取出多少石子都一定得到一个必胜局面

注意上方两点中“某个”和“任意”的区别，某个是指并非所有操作都可以达到上方所说的效果，但是一定有一个可以，而且题目要求可以保证每次都选择最优方案，所以一定可以选择到那个特定的操作；任意是指无论如何操作都一定会有那个效果，即使按照每次选择最优方案的策略都会有这样的效果

代码实现

只需要按照Nim定理进行判断即可

Nim游戏的推广

名词和定理

公平组合游戏 上述的Nim游戏实际为一个公平组合游戏(ICG: Impartial Combinatorial Games)，其满足几点特征~~(其实也就是了解一下，做题没啥用)~~

由两名玩家交替进行
在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关
不能行动的玩家判负(输)

有向图游戏 给定一个有向无环图，图中有唯一一个起点，在起点上放有一枚棋子。两名玩家交替将棋子沿着有向边移动，每次可以移动一次，无法移动者判定为输(判负)。如果将游戏过程中每一个局面(状态)看为图中的一个节点，局面的变化看为节点沿着有向边的移动，任意一个公平组合游戏都可以看为是一个有向图游戏。

mex运算 设S为一个非负整数集合，mex(S)含义为求出不属于集合S的最小非负整数，即： $mex(S) = \displaystyle \min_{x \ \in \ N, \ x \ \notin \ S}{x}$

SG函数 在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达$y_1, y_2, ..., y_k$，定义SG(x)为x的后继节点$y_1, y_2, ..., y_k$的SG函数值构成的集合执行mex的结果，即： $SG(x) \ = \ mex({SG(y_1), SG(y_2), \ ... \ ,SG(y_k)})$ 实际效果见下图：有向图游戏G的SG函数值定义为游戏起点的SG函数值。

有向图游戏的和 有向图游戏的和的SG函数值等于各个子游戏SG函数值的异或和(游戏的SG函数值概念见SG函数最后一行)

定理

有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值>0 有向图游戏某个局面必败，当且仅当该局面对应节点的SG函数值=0

原因在于SG函数值为0代表到达了不能行动的局面，自然对应着必败局面；SG函数值非0表示后续节点中包含终点，即可以使得对手到达不能行动的局面，则对应必胜局面

注意定理提到的只是一个子问题，比如只有一堆石子，每次可以拿固定数量的石子，询问先手是否必胜。根据最初节点的SG函数值即可判断初始节点是否为必胜态。但是实际问题一定都是多个子问题，比如有多堆石子，每次可以拿固定数量的石子，询问先手是否必胜。对于多个子问题，是否先手必胜取决于各个子问题SG函数值的异或和，即取决于有向图游戏的和，书中并没有证明该结论，只是提到与上述Nim游戏的证明类似，但是我暂时并没有想懂。

举例

给定n堆石子以及一个由k个不同正整数构成的数字集合S。现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合S，最后无法进行操作的人视为失败。问如果两人都采用最优策略，先手是否必胜。

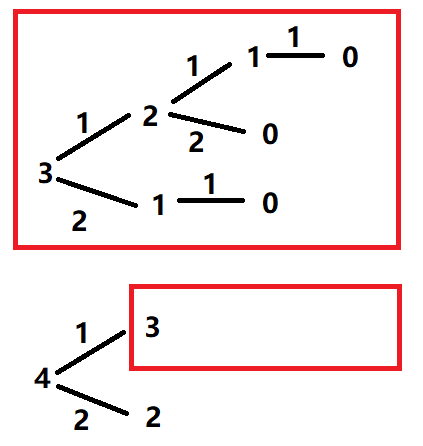
分析其实上面提到的Nim游戏可以看为是该题的特例，特殊在k=1，s中只有一个数据1。可以看出本题就是定理中提到的多个子问题的情况，解题关键在于求解出每一个子游戏的SG函数值，我们考虑时只需要考虑一个子游戏，然后遍历求解即可。对于某一个节点的SG，取决于其后续节点的SG，所以代码实现是递归。同时考虑到不同子游戏中相同状态的节点(状态在本题中指堆中石子数量)的SG其实是相等的，因为对于该节点而言，无论处于哪个子游戏中，它延伸出的后续节点都是一样的，根据SG函数的本质求解方式，不同子游戏相同状态的节点SG显然是相等的，所以递归采用记忆化来降低复杂度。对于记忆化的进一步解释可以查看下图，红色框的两部分目的都是计算石子数量为3对应节点的SG函数值，显然计算4会递归计算3，如果此前计算过3那么此时就没有必要再算一次了，能够记忆化的关键在于不同子游戏中相同状态节点的SG是相等的。

代码实现

/**
 * 在计算某节点的SG时需要先求解所有后续节点的SG，之后选择一个最小且不在这些SG值中的非负整数值
 * 实现方式很多，可以用数组存储然后从小到大排序并从小到大依次查看，第一个没有出现的数值就符合我们的要求，这样做时间复杂度的瓶颈在于排序，最快也要O(nlogn)
 * 但是我们在计算节点x的SG时，只需要判断某个值是否属于所有后续节点的SG值集合中，采用哈希是更好的方案
 * 如果使用STL，使用unordered_map和unordered_set均可，代码中注释部分为使用unordered_map的实现方式
 */
#include <iostream>
#include <unordered_map>
#include <unordered_set>
#include <cstring>

using namespace std;

const int N = 110, M = 10010;

int m, s[N];
int n, f[M]; // f[i]:石子数量为i对应的节点的SG函数值

int sg(int x)
{
    if (f[x] != -1) return f[x];
    
    unordered_set<int> S;
    // unordered_map<int, bool> S;
    for (int i = 0; i < m; ++ i)
        if (x >= s[i])
            S.insert(sg(x - s[i])); // 把x的所有后续节点的sg先存储下来
            // S[sg(x - s[i])] = true;
    
    // 找到不在集合中且最小的值作为x节点的SG值
    for (int i = 0; ; ++ i)
        if (!S.count(i)) // count：统计set中i的数量，由于set会去重，所以返回值为0或者1
        // if (!S[i]) 
            return f[x] = i;
}
int main()
{
    cin >> m;
    for (int i = 0; i < m; ++ i) cin >> s[i];
    cin >> n;
    
    memset(f, -1, sizeof f);
    int res = 0;
    while (n --)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    
    if (res) cout << "Yes" << endl;
    else cout << "No" << endl;
    
    return 0;
}

标签：总结,石子,xor,游戏,博弈论,必胜,SG,节点
From： https://blog.51cto.com/u_14882565/7082292