核函数估计
参考这里
-
Kernel Density Estimation, KDE
-
这个东西的目的在于使用离散的样本估计概率密度函数。
-
公式推导:
\[\begin{aligned} &1:\quad f(x)=\lim\limits_{h\to0}\frac{F(x+h)-F(x-h)}{2h}\\ &2:\quad\Rightarrow \hat{f}_h(x)=\frac{1}{2nh}\sum\limits_{i=1}^n1(x-h\le x_i\le x+h)\\ &3:\quad\quad=\frac{1}{nh}\sum\limits_{i=1}^n\frac{1}{2}1(\frac{|x-x_i|}{h}\le1)\\ &4:\quad\quad=\frac{1}{nh}\sum\limits_{i=1}^nK_0(\frac{x-x_i}{h}) \end{aligned} \]第1行来自于概率密度函数的定义,\(F(x)\)是概率分布函数;第2行是在仅有采样数据时对定义的近似,从定义出发看\(h\)越小越好,但\(h\)太小可能会使得区间内没有足够的点用于计算概率密度;第4行中的\(K_0\)在此处的推导中为\(K_0(t)=\frac{1}{2}1(|t|\le1)\)。这个函数不光滑,于是就想到把它替换掉,同时将其扩展到\(d\)维得情形,可以得到一般的形式:
\[\hat f(x)=\frac{1}{nh^d}\sum\limits_{i=1}^nK(\frac{x-x_i}{h}) \]替换的函数需要满足:
\[\begin{aligned} \int \hat{f}_h(x)=1&=\int\frac{1}{nh}\sum\limits_{i=1}^nK_0(\frac{x-x_i}{h})\mathrm d x\\ &=\frac{1}{n}\sum\limits_{i=1}^n\int K_0(\frac{x-x_i}{h})\mathrm d\frac{x-x_i}{h}\\ &=\frac{1}{n}\sum\limits_{i=1}^n\int K_0(t)\mathrm dt\\ &=\int K_0(t)\mathrm dt \end{aligned} \]所以只需要选取的\(K\)对概率空间积分为1就好。
-
常见的核函数\(K\)
假设\(x\)是\(d\)维向量,\(c_d\)是\(d\)维空间下单位球的体积。
上述的均匀分布函数:
\[K_0(x)= \left\{ \begin{aligned} &\frac{1}{c_d}&\text{if}\ x^Tx\le1\\ &0\quad&\text{otherwise} \end{aligned} \right. \]各阶导数都光滑的标准高斯:
\[K_G(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}x^Tx\right) \]以及Epanechnikov:
\[K_E(x)= \left\{ \begin{aligned} &\frac{d+2}{2c_d}(1-x^Tx)&\text{if}\ x^Tx\le1\\ &0\quad&\text{otherwise} \end{aligned} \right. \]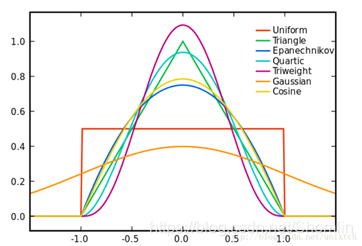
-
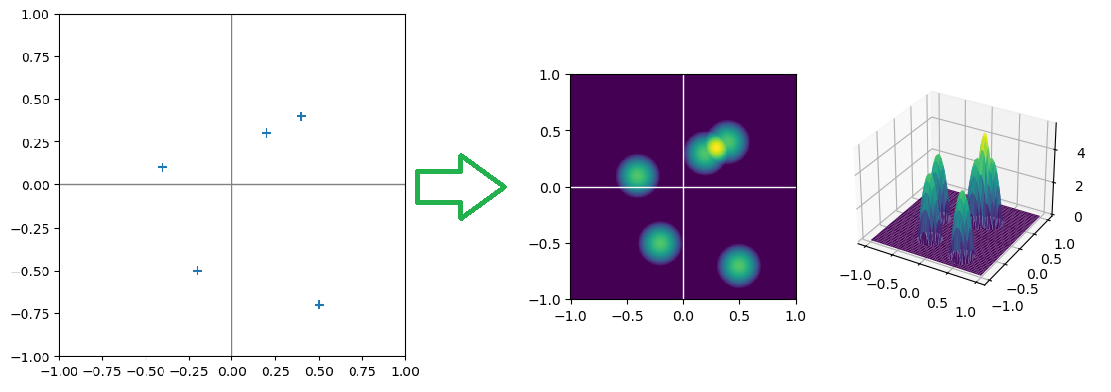
直观的图形化理解:相当于是在每个采样点\(x_i\)处放了个\(K(\frac{x-x_i}{h})\)的概率密度分布,然后叠加在一起就构成了估计出的概率密度分布。比如下图左侧是一个二维随机变量的采样数据(为了方便演示,采样点个数取的很少,\(h\)取得也比较小),右侧对这写数据用Epanechnikov核函数估计的概率密度分布: