首页 > 其他分享 >Codeforces Round 891 (Div. 3)

Codeforces Round 891 (Div. 3)

时间：2023-08-08 12:13:30浏览次数：42  
标签：891 连通 int siz sum Codeforces 数组 Div ll

A. Array Coloring

题意

给你 \(n(2\le n\le50)\) 个数，你可以把每个数染成红或蓝，求是否有方案满足每个颜色都有数而且两种颜色每个颜色内所有数之和的奇偶性相同。多组数据 \((t\le1000)\)。

例如：\([1,2,4,3,2,3,5,4]\) 染成 \([\color{blue}1,\color{blue}2,\color{red}4,\color{blue}3,\color{red}2,\color{red}3,\color{red}5,\color{red}4]\)，其中蓝色所有数之和是 \(6\)，红色所有数之和是 \(18\)，\(6\) 和 \(18\) 都是偶数。

题解

判断所有数之和的奇偶性即可。如果是偶数就是 Yes，如果是奇数就 No。

因为 \(n\ge2\)，所以如果 sum 是偶数，就绝对可以分解成 奇数 + 奇数 / 偶数 + 偶数。如果 sum 是奇数就不能这么分解。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
constexpr int N = 55;
int n, sum;
void solve() {
	scanf("%d", &n), sum = 0;
	for (int i = 1, x; i <= n; i++)
		scanf("%d", &x), sum += x;
	puts(sum & 1 ? "No" : "Yes");
}
int main() {
	int T; scanf("%d", &T);
	while (T--) solve();
	return 0;
}

B. Maximum Rounding

题意

给一个自然数 \(x\)，你可以把它四舍五入到第 \(k\) 位，可以多次四舍五入，求最大能四舍五入到多少。多组数据 \((t\le10^4)\)，\(x\) 的长度 \(\le2\cdot10^5\)。

例如：\(x=3451\)，那么

  • \(k=0\)，答案是 \(3451\)
  • \(k=1\)，答案是 \(3450\)
  • \(k=2\)，答案是 \(3500\)
  • \(k=3\)，答案是 \(4000\)
  • \(k=4\)，答案是 \(0\)

显然先是 \(k=2\) 再是 \(k=3\) 最大，是 \(4000\)。

题解

这个其实可以直接按从 \(k=0\) 到 \(k=len_x\) 模拟的。

实际上可能有个贪心，就是把所有可能进位的位给他进位。然后过程中记录一个 \(k\) 表示四舍五入到第 \(k\) 位，后面都输出 \(0\)。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e5 + 10;
char s[N];
int n, k;
void solve() {
	memset(s, 0, sizeof(s));
	scanf("%s", s + 1), n = strlen(s + 1), k = n;
	for (int i = n; i >= 1; i--) {
		if (s[i] <= '4') continue;
		s[i] = 48, s[i - 1]++, k = i;
	}
	if (s[0]) putchar(s[0] + 48);
	for (int i = 1; i <= n; i++)
		if (i <= k) putchar(s[i]);
		else putchar(48);
	puts("");
}
int main() {
	int T; scanf("%d", &T);
	while (T--) solve();
	return 0;
}

C. Assembly via Minimums

题意

有 \(n(n\le10^3)\) 个数的数组 \(a\)，经过两两取 \(\min\) 后得到长度 \(\frac{n\cdot(n-1)}2\) 的数组 \(b\)。现在给你 \(n\) 和打乱后的数组 \(b\)，求原数组 \(a\)，要求 \(a_i\in[-10^9,10^9]\)。多组数据，\(t\le200\)。

例如：\(a\) 数组是 \([2,3,5,1]\)，那么 \(b\) 数组就是 \([\min(2,3),\min(2,5),\min(2,1),\min(3,5),\min(3,1),\min(5,1)]=[2,2,1,3,1,1]\)。

现在给出 \(b\) 数组是 \([2,2,1,3,1,1]\)，那么 \(a\) 数组可以是 \([2,3,5,1]\)，也可以是 \([2,3,3,1]\)。

题解

首先你会发现，\(b\) 数组中出现过的数肯定在 \(a\) 数组也出现过。

于是把 \(b\) 数组排个序，观察当前最小值，发现：如果最小值在原数组中出现 \(1\) 次，那么它就在 \(b\) 数组中出现 \(n-1\) 次；出现 \(2\) 次则是 \((n-1)+(n-2)\) 次，出现 \(3\) 次是 \((n-1)+(n-2)+(n-3)\) 次……

于是就好了，每次输出一个数都让 n--，然后记录当前所有 \(n\) 的和……最终如果还有剩余，那么就一直输出 \(b\) 数组中的最大值就行了。

注意数组大小要开到 \(\frac{n\cdot(n-1)}2\)……还有 \(mx\) 初始值要设成 \(-\infty\) 而不是 \(0\)……交了两发罚时……

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1000010, inf = 0x3f3f3f3f;
int n, m, mx, a[N];
void solve() {
	memset(a, 0, sizeof(a)); mx = -inf;
	scanf("%d", &n), m = ((n * (n - 1)) >> 1);
	for (int i = 1; i <= m; i++)
		scanf("%d", &a[i]), mx = max(mx, a[i]);
	sort(a + 1, a + m + 1);
	for (int i = 1, cnt = 0; i <= m; i++) {
		if (a[i] != a[i - 1]) {
			int k = n - 1;
			while (k <= cnt) {
				printf("%d ", a[i - 1]);
				k += --n - 1;
			}
			cnt = 1;
		} else {
			cnt++;
		}
	}
	while (n--) printf("%d ", mx);
	puts("");
}
int main() {
	int T; scanf("%d", &T);
	while (T--) solve();
	return 0;
}

时间复杂度每次 \(\mathcal O(n+m),m=\frac{n\cdot(n+1)}2\)，本题中 \(\sum n\le10^3\)。

D. Strong Vertices

题意

给定两个 \(n(n\le2\cdot10^5)\) 个数的数组 \(a\) 和 \(b\)，构造一个有向图，其中每条有向边 \(u\to v\) 存在当且仅当 \(a_u-a_v\ge b_u-b_v\)，如果一个节点有连向其他所有节点的有向边，则称这个节点是强节点，求强节点数量以及所有强节点，按字典序输出。多组数据，\(t\le10^4,a_i,b_i\in[-10^9,10^9],\sum n\le2\cdot10^5\)。

例如：\(a\) 数组为 \([3,1,2,4]\)，\(b\) 数组为 \([4,3,2,1]\) 时，这个有向图长这样：

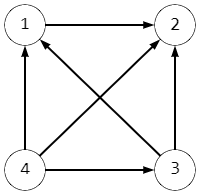
图片好像挂了……

只有 \(4\) 有连向 \(1,2,3\) 的有向边，因此强节点只有 \(4\)。

题解

首先肯定是把“强节点”转化一下。强节点满足有连向其他所有点的有向边，而一条有向边 \(u\to v\) 意味着 \(a_u-a_v\ge b_u-b_v\)，所以设这个节点为 \(i\)，那么对于所有 \(j\ne i\)，有 \(a_i-a_j\ge b_i-b_j\)，我们需要求出所有这样的 \(i\)。

然后就很简单啊，\(a_i-a_j\ge b_i-b_j\) 意味着 \(a_i-b_i\ge a_j-b_j\)，预处理出来所有的 \(a_i-b_i\)，求个最大值，把所有最大值的编号从小到大输出即可。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e5 + 10, inf = 0x3f3f3f3f;
int n, a[N];
void solve() {
	memset(a, 0, sizeof(a));
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	for (int i = 1, x; i <= n; i++)
		scanf("%d", &x), a[i] -= x;
	int mx = -inf, cnt = 0;
	for (int i = 1; i <= n; i++)
		mx = max(mx, a[i]);
	for (int i = 1; i <= n; i++)
		if (a[i] == mx) cnt++;
	printf("%d\n", cnt);
	for (int i = 1; i <= n; i++)
		if (a[i] == mx) printf("%d ", i);
	puts("");
}
int main() {
	int T; scanf("%d", &T);
	while (T--) solve();
	return 0;
}

E. Power of Points

题意

数轴上有 \(n(n\le2\cdot10^5)\) 个点 \(x_i(1\le x_i\le10^9)\)。对于数轴上任意一点 \(y\)，它都有 \(n\) 条线段满足两端点分别为 \(x_i\) 和 \(y\)。每条线段 \([a,b]\) 覆盖了 \(a,a+1,\dots,b\) 这些点，而对于数轴上任意一点 \(p\)，定义贡献 \(f_p\) 为它被线段覆盖的次数。你需要对于每个 \(y=x_i\) 求出 \(\sum f_p\)。多组数据，\(t\le10^4,\sum n\le2\cdot10^5\)。

例如：\(x=[1,2,5,7,1]\)，此时 \(y=5\)，那么就会有这些线段：\([1,5],[2,5],[5,5],[5,7],[1,5]\)，那么 \(f_1=2,f_2=3,f_3=3,f_4=3,f_5=5,f_6=1,f_7=1,f_8=0,\dots,f_{10^9}=0\)，所以 \(\sum f=2+3+3+3+5+1+1=18\)。

题解

首先把 \(\sum f_p\) 转化一下，我们知道一条线段 \([a,b]\) 就会使 \(\sum f_p\) 加上 \((b-a+1)\)，因为这些点的 \(f\) 都加了 \(1\)，而 \(\sum f_p\) 原先为 \(0\)。所以 \(\sum f_p\) 就是线段覆盖的点的数量之和。

把 \(x_i\) 排个序，然后因为 \(n\) 条线段就有 \(n\) 次 \((b-a+1)\)，把所有讨厌的 \(+1\) 放到最后变成 \(+n\)，就不用在中途考虑 +1 了。

然后就是分前后讨论，假设当前 \(y=x_i\)，那么对于所有 \(j<i\)，\(x_j<x_i\)，所有线段形如 \([x_j,x_i]\)，答案就是 \(\sum(x_i-x_j)=\sum x_i-\sum x_j=x_i\cdot(i-1)-pre_{i-1}\)，其中 \(pre\) 表示前缀和。对于 \(j>i\) 同理。

于是预处理前后缀和然后直接算就完了。注意存储每个数原来的位置好存储答案。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
constexpr int N = 2e5 + 10;
struct Data {
	ll val; int id;
} a[N];
ll ans[N], pre[N], suf[N];
int n;
void solve() {
	scanf("%d", &n), suf[n + 1] = 0;
	for (int i = 1; i <= n; i++)
		scanf("%lld", &a[i].val), a[i].id = i;
	sort(a + 1, a + n + 1, [&](const Data& x, const Data& y) -> bool {
		return x.val < y.val;
	});
	for (int i = 1; i <= n; i++)
		pre[i] = pre[i - 1] + a[i].val;
	for (int i = n; i >= 1; i--)
		suf[i] = suf[i + 1] + a[i].val;
	for (int i = 1; i <= n; i++) 
		ans[a[i].id] = suf[i + 1] - 1LL * a[i].val * (n - i) + 1LL * a[i].val * (i - 1) - pre[i - 1];
	for (int i = 1; i <= n; i++)
		printf("%lld%c", ans[i] + (ll)n, " \n"[i == n]);
}
int main() {
	int T; scanf("%d", &T);
	while (T--) solve();
	return 0;
}

注意 long long。。。

F. Sum and Product

题意

给定 \(n\) 个数的数组 \(a_i\)，\(q\) 次询问，每次给一个 \(x\) 和 \(y\)，问同时满足 \(a_i+a_j=x\) 以及 \(a_i\cdot a_j=y\) 的 \(i\) 和 \(j(i<j)\) 的个数。其中 \(n\le2\cdot10^5,1\le|a_i|\le10^9,q\le2\cdot10^5,1\le|x|\le2\cdot10^9,1\le|y|\le10^{18}\)，多组数据，\(t\le10^4,\sum n,q\le2\cdot10^5\)。注意负数。

例如，假设原数组是 \([1,3,2]\)，询问的 \(x=3,y=2\)，答案是 \(1\)：

  • \(i=1,j=2\) 不行因为 \(1+3=4\) 而不等于 \(3\)，同时 \(1\cdot3=3\) 而不是 \(2\)；
  • \(i=1,j=3\) 同时满足两个条件；
  • \(i=2,j=3\) 不行因为 \(3+2=5\) 而不等于 \(3\)，同时 \(3\cdot2=6\) 而不是 \(2\)。

题解

初中知识，假如 \(a+b=x,a\cdot b=y\)，那么

  • \(a^2+2ab+b^2=(a+b)^2=x^2\)；
  • \(a^2-2ab+b^2=(a+b)^2-4ab=x^2-4y\)；
  • \(a-b=\sqrt{(a-b)^2}=\sqrt{a^2-2ab+b^2}=\sqrt{x^2-4y}\)。

设 \(\sqrt{x^2-4y}=z\)，那么 \(a=\frac{x+z}2,b=x-a\)。于是就算出来了 \(a\) 和 \(b\)。（如果有任意一步不是整数，就直接输出 \(0\)）

然后直接用 map 存储每个数的出现次数。直接算。

注意 \(a=b\) 时需要满足 \(i<j\)，所以此时答案是 \(\frac{cnt_a\cdot(cnt_a-1)}2\)。然后用 long long 输出。就没了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
constexpr int N = 2e5 + 10;
map<int, int> b;
int n, q;
ll a[N];
void solve() {
	b.clear();
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%lld", &a[i]);
		if (!b.count(a[i])) b[a[i]] = 1;
		else b[a[i]]++;
	}
	scanf("%d", &q);
	while (q--) {
		ll x, y; scanf("%lld%lld", &x, &y);
		ll k = 1LL * x * x - 4LL * y;
		ll z = (ll)sqrt(k);
		if (1LL * z * z != k) {
			printf("0 "); continue;
		}
		if ((z + x) & 1) {
			printf("0 "); continue;
		}
		ll ai = (z + x) >> 1, aj = ai - z;
		if (b.count(ai) && b.count(aj)) {
			if (ai != aj) printf("%lld ", 1LL * b[ai] * b[aj]);
			else printf("%lld ", 1LL * b[ai] * (b[ai] - 1) >> 1);
		} else printf("0 ");
	}
	puts("");
}
int main() {
	int T; scanf("%d", &T);
	while (T--) solve();
	return 0;
}

G. Counting Graphs

题意

给出一棵 \(n(n\le2\cdot10^5)\) 个节点的树，其中每条边有边权 \(w_i\)，以及一个数 \(S(1\le S\le10^9)\)。求最小生成树恰好是这棵树且每条边权 \(\le S\) 的简单无向图的数量，对 \(998244353\) 取模。\(w_i\le S\)，多组数据，\(t\le10^4,\sum n\le2\cdot10^5\)。

更详细的题意 给出一个 $n$ 个节点的树，其中每条边有权值 $w_i$。

你的任务是数满足以下四个条件的无向图的数量：

  1. 没有重边、自环。
  2. 每条边的权值是正整数且 \(\le S\)。
  3. 这张图有恰好一棵最小生成树。
  4. 这棵最小生成树就是给定的树。

两张图被认为是不同的当且仅当它们的边集不同（包括端点、权值）。

由于答案可能会很大，所以你需要把它对 \(998244353\) 取模。

多组数据，\(t\le10^4,2\le n\le2\cdot10^5,1\le S\le10^9,1\le w_i\le S, \sum n\le2\cdot10^5\)。

例如：\(n=4,S=5\)，给定的树长这样：

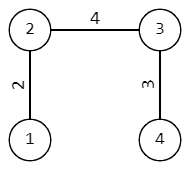
图片好像挂了……

那么有 \(8\) 种可能的无向图（红边代表最小生成树的边）：

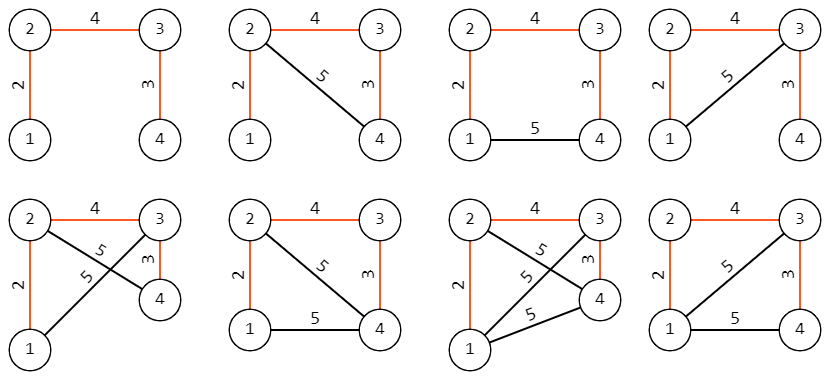
图片好像挂了……

题解

根据 Kruskal 最小生成树的思想，我们可以先把树边按边权从小到大排好序，然后一条一条地加进去，看答案发生的变化。

由于最终形成的是一棵树，所以每次加进来的边是一定不会形成环的，而是连接两个不同的连通块，初始时所有 \(n\) 个节点互不连通。

假设我们当前加入了一条无向边 \((u,v,w)\)，那么这条边连接了 \(u\) 所在的连通块以及 \(v\) 所在的连通块，所以我们当前应该考虑在 \(u\) 连通块和 \(v\) 连通块之间多加一些边形成一个无向图，那么我们多加的边权应该是 \((w+1)\sim S\)，因为假如这是第一条加入的边，那么比它小或者等于它的边权是一定不可取的，不然最小生成树就不会恰好是给定的树了，而假如这不是第一条加入的边，比它小的边权已经在前面考虑过了，所以我们当前加入的边权一直在 \([w+1,S]\) 这段区间内的。

为什么我们只考虑在连通块之间连边而没有考虑连通块内部连边呢？因为我们考虑的仅仅是当前加入的边所造成的影响，而连通块内部的连边已经在我们之前连通块内部被一条边连通的时候计算过了，所以我们不用考虑这个内部的答案连边。

计算答案的方式就是每次乘以当前可选的方案数。假设当前 \(u,v\) 的连通块的大小分别为 \(siz_u\) 和 \(siz_v\)，那么一共可以连 \(siz_u\cdot siz_v\) 条边，除去原有的一条生成树边就是 \(siz_u\cdot siz_v-1\)。每条边可以是 \([w+1,S]\) 或者不连这条边，所以当前总影响就是 \((S-w-1+1+1)^{siz_u\cdot siz_v-1}=(S-w+1)^{siz_u\cdot siz_v-1}\)。

如何快速维护连通块信息呢？直接并查集呗，在维护的同时把该连通块的信息一块儿存储在根上面，到时候直接 getfather 查询即可。

当时由于没打 cf 经验太困了脑壳疼就直接睡觉去了。。。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
constexpr int N = 2e5 + 10, MOD = 998244353;
struct edge {
	int u, v, w;
} e[N];
int n, fa[N], siz[N]; // in root
ll ans, S;
int getfa(int u) {
	return u == fa[u] ? u : fa[u] = getfa(fa[u]);
}
inline ll qpow(ll x, ll y) {
	ll res = 1;
	while (y) {
		if (y & 1) res = res * x % MOD;
		x = x * x % MOD, y >>= 1;
	}
	return res;
}
void solve() {
	scanf("%d%lld", &n, &S); ans = 1;
	for (int i = 1; i < n; i++)
		scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
	for (int i = 1; i <= n; i++) fa[i] = i, siz[i] = 1;
	sort(e + 1, e + n, [&](const edge& x, const edge& y) {
		return x.w < y.w;
	});
	for (int i = 1; i < n; i++) {
		int u = e[i].u, v = e[i].v;
		int fu = getfa(u), fv = getfa(v);
		int su = siz[fu], sv = siz[fv];
		if (fu != fv) siz[fu] += siz[fv], fa[fv] = fu;
		ans = (ans * qpow(S - e[i].w + 1, 1LL * su * sv - 1)) % MOD;
		// huan++ (here including EMPTY)
	}
	printf("%lld\n", ans);
}
int main() {
	int T; scanf("%d", &T); while (T--) solve();
	return 0;
}

写水题题解真爽。。。

标签：891,连通,int,siz,sum,Codeforces,数组,Div,ll
From： https://www.cnblogs.com/laijinyi/p/17613815.html

相关文章

  • 滚动到顶div块固定左侧不动
    <scripttype="text/javascript">$(function(){//获取要定位元素距离浏览器顶部的距离varnavH=$(".t_left").offset().top;//滚动条事件$(window).scroll(function(){//获取滚动条的滑动距......
  • Codeforces Round 890 (Div. 2) supported by Constructor Institute A-E1
    An=50非常小所以直接暴力枚举枚举每次把某个数以下的全部减完然后看一下是否上升就行 https://codeforces.com/contest/1856/submission/217275334  B题直接贪心前面优先放最小的最后一个放最大的 然后如果重复了就到前面去看能不能调整一下 https://codeforces.......
  • 国产化SCT52241双通道下管IGBT/MOSFET栅极驱动器，可替代UCC27525A、ISL89165等
    SCT52241是是一款宽供电电压、双通道、高速、低测栅极驱动器，包括功率MOSFET，IGBT。单个通道能够提供高达4A拉电流和4A灌电流的轨到轨驱动能力，并实现轨到轨输出。高达24V宽电压范围提高功率器件开关瞬间栅极驱动的振铃幅值裕度。13ns输入输出传输延迟特性适合高频功率转换器应用。SCT......
  • Codeforces Round 890 (Div. 2)
    A.TalesofaSort题目大意Alphenhasanarrayofpositiveintegers\(a\)oflengthn.Alphencanperformthefollowingoperation:Forall\(i\)from1ton,replace\(a_i\)with\(\max(0,a_i−1)\).Alphenwillperformtheaboveoperationuntil\(......
  • Codeforces Round #890 Div.2
    link题号：1856A~E2A题面：给定一个正整数\(n\)和一个长度为\(n\)的序列\(a\)，重复执行以下操作直至\(a\)序列单调不减：\(\forall1\lei\len\)，\(a_i=\max(a_i-1,0)\)。求一共需要执行多少次操作。多测，共\(t\)组数据。对于所有数据，保证\(1\let\le500\)......
  • Codeforces Round 890 (Div. 2) A-E1
    A.TalesofaSort题意：给出一个长为n的数组a，每次操作可以使得所有的数-1，最小不会小于0，问至少需要多少次操作才能使得a变得有序。Solution把数组a排序，从大到小遍历，如果当前的\(a[i]\)不是原来的话，那么要想让它有序，必须进行当前的\(a[i]\)次操作，这样才能使得它有序voidsolve()......
  • 【LGR-148-Div.3】洛谷基础赛 #1 & MGOI Round I
    【LGR-148-Div.3】洛谷基础赛#1&MGOIRoundIT1luoguP9502『MGOI』SimpleRoundI|A.魔法数字\(100pts\)水题，场切了。#include<bits/stdc++.h>usingnamespacestd;#definelllonglong#definesortstable_sort#defineendl'\n'intmain(){ ......
  • Codeforces Round 890 (Div. 2) supported by Constructor Institute
    Preface现在开始严格按照双号上分法来打CF了，大致就是每次比赛都拿两个号中分较少的那个打，这样可以保证两个号的最高分不降然后昨天打完就后悔了，没有拿hl666那个号打导致没抓住难得的上分机会，本来可以打到橙名渡劫局的但分全加在Kusanagi_Misuzu那个号上了不过昨天这场其实可以......
  • 【题解】Codeforces Round 890（CF1856）
    赛时过了A-E1，rk195可惜是E2傻逼了不会背包优化了，直接连普及组水平都不到了。A.TalesofaSort题目描述：给定长度为\(n\)的序列\(a\)，每次操作为对于所有\(i\)将\(a_i\)变为\(\max(a_i-1,0)\)，询问最少多少次操作之后可以让序列\(a\)单调不降。题目分析：唯一能改变......
  • 【LGR-148-Div.3】洛谷基础赛 #1 & MGOI Round I
    【LGR-148-Div.3】洛谷基础赛#1&MGOIRoundI据说是普及组难度？T1P9502『MGOI』SimpleRoundI|A.魔法数字\(100pts\)题目描述初级魔法士小M的魔法数字是\(2\)。给定一个正整数\(n\)，小M需要找到最大的偶数\(m\)，使得\(2^m<n\)。又双叒叕是个水题，然后被又双......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99