发现之前学的真的一塌糊涂呢(/ω\)
很多非常精髓的地方理解的都不够好,比如说为啥我要用一棵 dfs 树来为框架,跑 tarjan?这里我就理解的不好,所以我来重新写一篇,加深加深印象。
以下一切默认为无向图。
0. 基本概念
这里面说的非常不严谨,只是为了方便理解啦 awa
- 连通分量:你可以简单的理解为连通块
- dfs 树:我们可以 dfs 一张图,我们 dfs 会形成一棵树。
- dfs 序:dfs 树中每个点是被第几个 dfs 到的。\(dfn(u)\) 代表 \(u\) 的 dfs 序。
- 树边:在 dfs 树上的边。
- 反向边:不在 dfs 树上的边。我们很容易发现一点,如果 \((u, v)\) 不在 dfs 树上,那么 \(u\) 一定是 \(v\) 的祖先,这个很容易用反证法证明
1. 割点与桥
割点是什么嘞?比如说我删掉一个点,这个图的连通块数量就变多了。这个点就叫割点。
这个东西和连通性有关,和连通性有关的问题经常用 dfs 树,因为有棵树的话,那么我们在其中删去任何一个点/边这棵树都会不连通。那么对于一张图 \(G\),我们先变出来它的 dfs 树 \(T\)。我们假定这个 \(G\) 是连通图。
我们来考虑 \(u\) 点是不是割点:
- \(u\) 是根。
容易发现只要 \(u\) 点有两个以上的子树,那么 \(u\) 就是割点。 - \(u\) 不是根。
定理:非根节点 \(u\) 是割点,当且仅当 \(u\) 的儿子里面有一个点 \(v\) 满足 \(v\) 的子树中(含 \(v\))无法通过一条反向边走到 \(u\) 的祖先节点(不包括 \(u\)),那么 \(u\) 是 \(G\) 的一个割点。
证明:酱紫一张图。我们再次达成共识,返祖边 \((u, v)\) 一定是祖先和后代关系,不可能有一条边会跨 dfs 的两棵子树,手玩一下就可以了 qwq
第一张图就是 \(v\) 和它子树没有一条反向边连到 \(u\) 的祖先,那么这个时候只可能在 \(v\) 子树内部狂暴连边,那么删掉 \(u\) 很显然子树 \(v\) 就会变成一个新连通分量、
第二张图是 \(v\) 的子树里面有一条边连到了 \(u\) 本身,不过这也无济于事删掉 \(u\) 后子树 \(v\) 还是会变成一个新的连通分量。
第三张图是 \(v\) 的子树里面有一条边连到了 \(u\) 的祖先,很显然 \(u\) 不是割点。
dfs 树只有树边和反向边,所以只有上面三种情况,证毕。
那么问题就变成了,如何快速判断子树 \(v\) 连一条边能否走到 \(u\) 的祖先。
还记得 dfs 序吗?再次强调,在 dfs 树中没有一条边能够横跨两个子树。也就是说 \((u, v)\) 一定是祖先/后代关系(包括父子关系)。如果 \(u\) 为 \(v\) 祖先,那么一定有 \(dfn(u) < dfn(v)\)。有了 \(dfn\) 还不够,我们还可以定义一个 \(low\)。\(low(u)\) 为点 \(u\) 的子树中走一条边能连到的最早的祖先的 \(dfn\) 值。我们就可以这样重新写 \(u\) 不是根的割点判定条件:如果 \(u\) 有一个子节点 \(v\) 满足 \(low(v)\ge dfn(u)\),那么 \(u\) 是割点。
唯一的问题就在于 \(low(u)\) 怎么求了。这也比较容易
- \((u, v)\) 为树边(\(u\) 是父亲),那么 \(low(u) = \min\{low(v)\}\)。
- \((u, v)\) 为返祖边,(\(v\) 是祖先),那么 \(low(u) = \min\{low(v), dfn(u)\}\)。
值得一提的是,有向图的 tarjan 算法 low 的更新与此不同,有些人对此提出了疑惑,我个人感觉这就是对算法理解不好,我之前就这样 qwq(*/ω\*)
代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5;
vector <int> gra[MAXN + 10];
bool vis[MAXN + 10], chk[MAXN + 10];
int DFN = 0, dfn[MAXN + 10], low[MAXN + 10], root;
void dfs(int u, int fa) {
dfn[u] = low[u] = ++DFN;
int child = 0;
for(int p = 0; p < gra[u].size(); p++) {
int v = gra[u][p];
if(!dfn[v]) {
child++; dfs(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u] && u != root) chk[u] = 1;
}
else if(v != fa) low[u] = min(low[u], dfn[v]);
}
if(child >= 2 && u == root) chk[u] = 1;
}
void init() {
int n, m; cin >> n >> m;
for(int p = 1; p <= m; p++) {
int x, y; cin >> x >> y;
gra[x].push_back(y);
gra[y].push_back(x);
}
for(int p = 1; p <= n; p++) {
if(!dfn[p]) {
root = p;
dfs(p, p);
}
}
int cnt = 0;
for(int p = 1; p <= n; p++)
if(chk[p])
cnt++;
cout << cnt << endl;
for(int p = 1; p <= n; p++)
if(chk[p]) cout << p << ' ';
}
int main() {
init();
}
请注意我们特别记录了 \(u\) 点的父亲 \(fa\),这样可以防止把树边误判成反向边。在割点中不记录它是可以的,因为我们走树边会吧 \(low(v)\) 变成 \(dfn(u)\),但是这对 \(low(v) \le dfn(u)\) 没有影响。不过对割边是有影响的,为了规范最好记录。
相应的,割边是什么嘞,如果我把一条边删掉,连通分量变多了,那么这条边就叫割边。
我们会发现割边这东西长得真的和我们的个点很像,定理如下
对于图 \(G\) 的 dfs 树 \(T\) 中任意一个节点 \(u\),如果有一个子节点 \(v\),满足 \(v\) 的子树(含 \(v\))没有一条边可以连到 \(u\) 的祖先(包括 \(u\)),那么 \((u, v)\) 就是割边。
其实和上面的证明差不多,就是 \(u\) 的情况变了,那么用 dfn 和 low 刻画就是 \(low(v) > dfn(u)\)。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5;
struct piar {
int x, y;
} Q[MAXN + 10];
int cnt = 0;
bool cmp(piar &a, piar &b) {
if(a.x != b.x) return a.x < b.x;
else return a.y < b.y;
}
vector <int> gra[MAXN + 10];
int dfn[MAXN + 10], low[MAXN + 10], DFN = 0;
void dfs(int u, int fa) {
dfn[u] = low[u] = ++DFN;
for(int p = 0; p < gra[u].size(); p++) {
int v = gra[u][p];
if(!dfn[v]) {
dfs(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > dfn[u]) {
Q[++cnt].x = min(u, v);
Q[cnt].y = max(u, v);
}
}
else if(v != fa) low[u] = min(low[u], dfn[v]);
}
}
void init() {
int n, m; cin >> n >> m;
for(int p = 1, x, y; p <= m; p++) {
cin >> x >> y;
gra[x].push_back(y);
gra[y].push_back(x);
}
for(int p = 1; p <= n; p++)
if(!dfn[p])
dfs(p, p);
sort(Q + 1, Q + cnt + 1, cmp);
for(int p = 1; p <= cnt; p++)
cout << Q[p].x << ' ' << Q[p].y << endl;
}
int main() {
init();
}
2. 点双和边双
对于一个无向图,如果它没有个点,就叫点双连通图,如果没有割边,就叫边双连通图。
对于一个无向图,它的极大点双连通子图叫点双连通分量,简写为 v-DCC,简称为点双,极大边双连通子图叫边双连通分量,简写为 e-DCC。
点双性质:
定理:如果一张图是点双连通图,那么它一定满足下面的其中一条
- 节点数不超过两个
- 任意两个点都在一个简单环中。
证明:
1 显然成立。下面我们证明 2
还记得割点的判定法则吗:当一个非根节点 \(u\),如果满足有一个儿子 \(v\),\(v\) 及其子树无法通过一条边走到 \(u\) 的祖先(不包括 \(u\)),那么 \(u\) 是割点。反过来,如果 \(u\) 满足所有的儿子都能通过一条边走到 \(u\) 的祖先(不包括 \(u\)),那么 \(u\) 就不是割点。对于根节点,有两个以上儿子就是割点,所以对于一个 v-DCC 根节点只有一个儿子。
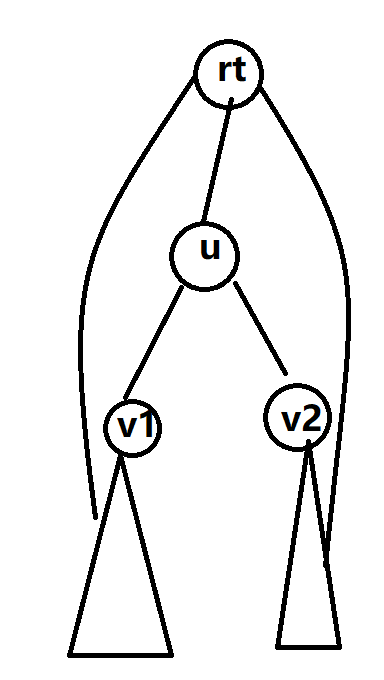
我们就可以这样画一个图。\(v1,v2\) 是 \(u\) 的儿子,当然 \(u\) 可能有很多儿子。对于 \(v\) 的子树,所有的点都可以通过一条边走到 \(u\) 的祖先。下面我们令 \(rt\) 为根,\(u\) 是根唯一的一个儿子。
(我个人感觉画出来图了就很显然了)我们只需要讨论四类点:\(rt\),\(u\),\(v1\) 及其子树里面的点,记为 \(x\),\(v2\) 及其子树里面的点,记为 \(y\)。
看上去我们要讨论很多,但实际上并不是。对于 \(rt\) 很显然满足,\(u\) 也一样。
那么 \(x, y\) 呢?也很容易,环是 \(x-v1-u-v2-y-rt-x\),这样就能有环了!
如果在一个子树里面有 \(x, x'\),那么就有 \(x-rt-x'-v1-x\),也有环。
综上所述,证毕
边双性质:
定理:对于一个边双连通图,每条边都在一个简单环里。
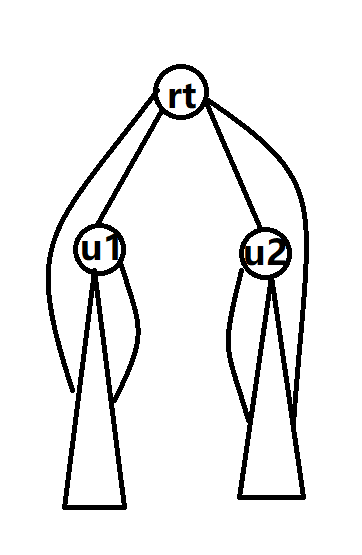
标签:tarjan,子树,int,双和边,dfs,割点,dfn,笔记,low From: https://www.cnblogs.com/thirty-two/p/17597173.html证明:和点双相同的道理,但是这次可能可以连到 \(u\) 自己了。所以我们可以这样画图
这张图甚至不用配文字,很显然这些边都可以花在一个环里面吧,具体过程就懒得写了(