东方博宜 2166 - 子树的大小及深度

题目描述

现在有一棵 n 个结点的树，结点 1为这棵树的根，结点 1 的深度为 1，求出每棵子树的大小及每个结点的深度。

比如，有如下图所示的树：

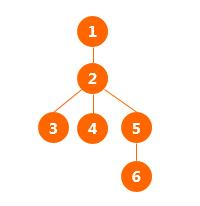
该树中：

结点 1 对应的子树大小为 6，深度为 1。

结点 2 对应的子树大小为 5，深度为 2。

结点 3 对应的子树大小为 1，深度为 3。

结点 4 对应的子树大小为 1，深度为 3。

结点 5 对应的子树大小为 2，深度为 3。

结点 6 对应的子树大小为 1，深度为44。

输入有 n 行。

第 1 行有一个整数 n，代表结点的数量，结点的编号为1∼n。（1≤n≤100)

接下来有 n−1行，每行有 2 个整数 x,y，表示结点 x 和 y 之间有一条边。（不保证 x 是 y 的父）

输出有 n行。

第 i 行输出 2 个整数，分别是以编号 i为根的子树的大小，以及编号 i 对应的结点的深度。

输入

6
1 2
5 2
2 3
4 2
5 6

输出

6 1
5 2
1 3
1 3
2 3
为什么东方博宜OJ不给看错误数据啊？我一题改1小时不知道错在哪，跟坐牢一样。
思路：

• 首先输入的x,y不保证x是y的父，那意思就是无向边了。
• 求深度不难想到是dfs，该点的深度就是自己的父节点的深度+1
• 求子树就得要递归了，遍历每一个自己可以到的点（除了父节点，这就相当于走回去了），然后把他们的子树大小加起来就行

由于遍历每一个自己可以到的点，在求深度的时候也需要进行此操作，两个步骤可以合并在同一个函数里

代码：

#include<iostream>
#include<vector>
using namespace std;
//存储深度和子树大小
int deep[105],treesize[105];
int n,x,y;
//不确定每个节点有几个子节点，用vector节省空间
vector <int> a[110];
//x：当前节点，f：父节点
int dfs(int x,int f){
    //当前节点子树大小初始化为1
    treesize[x]=1;
    //x的深度为父节点+1
    deep[x]=deep[f]+1;
    //遍历每一个x可以去的点
    for(int i=0;i<a[x].size();i++){
        //除了自己的爹
        if(a[x][i]!=f){
            //递归
            treesize[x] += dfs(a[x][i],x);
        }
    }
    //返回x的子树大小
    return treesize[x];
}
int main(){
    scanf("%d",&n);
    //读入数据
    for(int i=1;i<n;i++){
        scanf("%d%d",&x,&y);
        a[x].push_back(y);
        a[y].push_back(x);
    }
    dfs(1,0);
    //输出
    for(int i=1;i<=n;i++){
        printf("%d %d\n",treesize[i],deep[i]);
    }
    return 0;
}