本文仅发布于此博客和作者的洛谷博客,不允许任何人以任何形式转载,无论是否标明出处及作者。
前置废话
fhq为什么是神。
首先我们有一个正常Treap。
正常Treap对于每一个值引入了一个随机的键,在节点的值形成一个BST的基础上,保证键形成一个小根堆。也就是把这一个BST做成了笛卡尔树。
因为这个键是随机给的,所以树退化成链的形状的概率极其小,使得树深度期望是\(\log n\)级别的,从而避免了被毒瘤数据卡掉。
因为正常通过旋转维护小根堆的Treap码量较大,所以有了无旋Treap,即FHQ-Treap。FHQ-Treap好想好写,但是缺点也很明显,就是常数很大。我的实现甚至比Splay还要慢一倍。
Split操作
Split和下面的Merge为FHQ-Treap的两个最基本操作,其他操作都是在其基础上实现的。
Split的作用是给定一个数值\(x\),把一整棵树拆成分开的两棵树,一棵所有节点的值\(\leq x\),一棵节点的值\(>x\)。
Split是递归进行的:
设当前节点编号为\(k\)。如果其值\(\leq x\),则把\(k\)放在\(\leq x\)的树中。因为\(k\)的左子树中所有节点的值都\(<k\),所以\(k\)的整个左子树也应该放在\(\leq x\)的树中。
把其右子树拆开。右子树被拆成\(\leq x\),\(>x\)的两棵树。把\(k\)的右子树更新成拆出来的\(\leq x\)的那棵树,我们就把以\(k\)为根的树拆成了两棵:以\(k\)为根,\(\leq x\)的一棵,和从右子树拆出来的\(>x\)那棵。
如果\(k\)的值\(>x\),相似地,拆开左子树。把\(k\)的左子树更新成拆出来的\(>x\)的那棵树,同样把以\(k\)为根的树拆成了两棵:从左子树拆出来的\(\leq x\),以\(k\)为根的\(>x\)。
纯文字不太好理解,我们举个例子,拆掉下面这棵树。
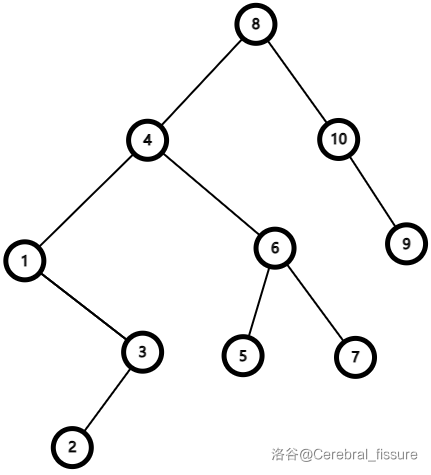
为了方便,每个节点的编号就是其权值。我们要把这棵树拆成\(\leq5\),\(>5\)两棵分开的树。(节点\(9\)应该是\(10\)的左儿子。无所谓,不影响理解算法。)
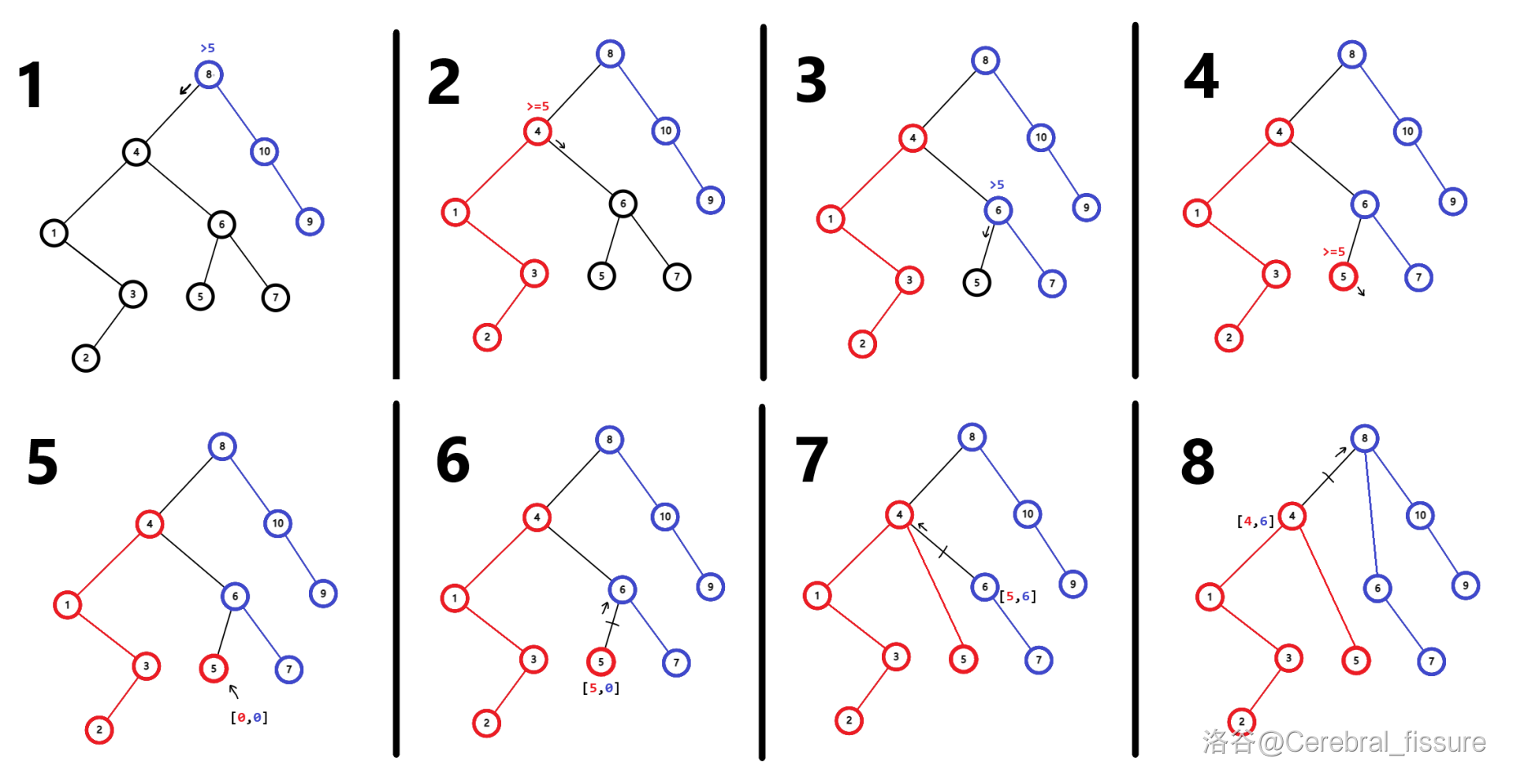
红色树为\(\leq 5\)的树,蓝色为\(>5\)的树。
注意到,第4步以后到了不存在的空节点。此时直接返回并记两棵树的树根都为\(0\)。
最后,这棵树就被分成了这个样子。
这个例子里并没有展示节点的键,但是因为Split没有颠倒点之间的父子关系(即一个点的祖先Split后不会到其子树里),所以不需要考虑键。
思路写成代码如下。
struct FHQ_Treap{
int key;//随机键
int val;//真实值
int lc;
int rc;
int size;//子树大小
}t[100005];
struct S{//S for Split,当然直接用pair<int,int>也可以
int Lroot;//split操作分出的<=x的树的根
int Rroot;//>x
};
S split(int x,int k){//在以k为根的树中,把值<=x和>x的节点拆成两棵树
if(k==0){//没有这个节点
return S{0,0};
}
if(t[k].val<=x){//k应该被分到<=x的树中
S tmp=split(x,t[k].rc);//递归拆k的右子树,左子树一定在<=x中
t[k].rc=tmp.Lroot;//认领下面拆出来的<=x的树为右子树
update(k);//更新size
return S{k,tmp.Rroot};//返回拆好的两棵子树
}else{//k应该被分到>x的树中,以下操作基本同上。
S tmp=split(x,t[k].lc);
t[k].lc=tmp.Rroot;
update(k);
return S{tmp.Lroot,k};
}
}
这里的update()不重要。
Merge操作
既然把树拆开了,就需要它们缝回去。Merge的作用就是缝合两棵树(保证一棵树中的所有节点的值都比另一棵的节点的值小)。
Merge也通过递归实现。
设\(k_1\)为值较小的树的根节点,\(k_2\)为较大的树的根节点。如果\(k_1\)的键比\(k_2\)小,那\(k_2\)为根的一整棵子树应该全放在\(k_1\)的右子树上。递归缝合到\(k_1\)的右子树上。
如果\(k_1\)的键比\(k_2\)大,\(k_1\)为根的一整棵子树应该放在\(k_2\)的左子树上。同样递归。
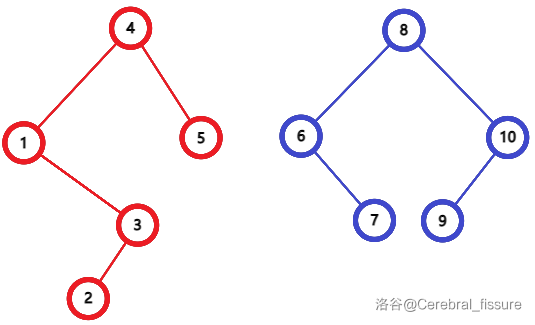
举例子,把上面分开的两棵树合并在一起。
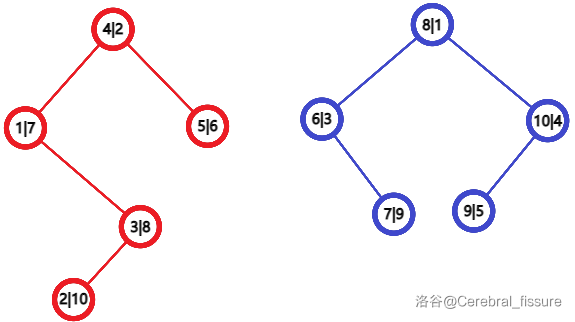
每个节点有两个数,第一个是值,第二个是键。
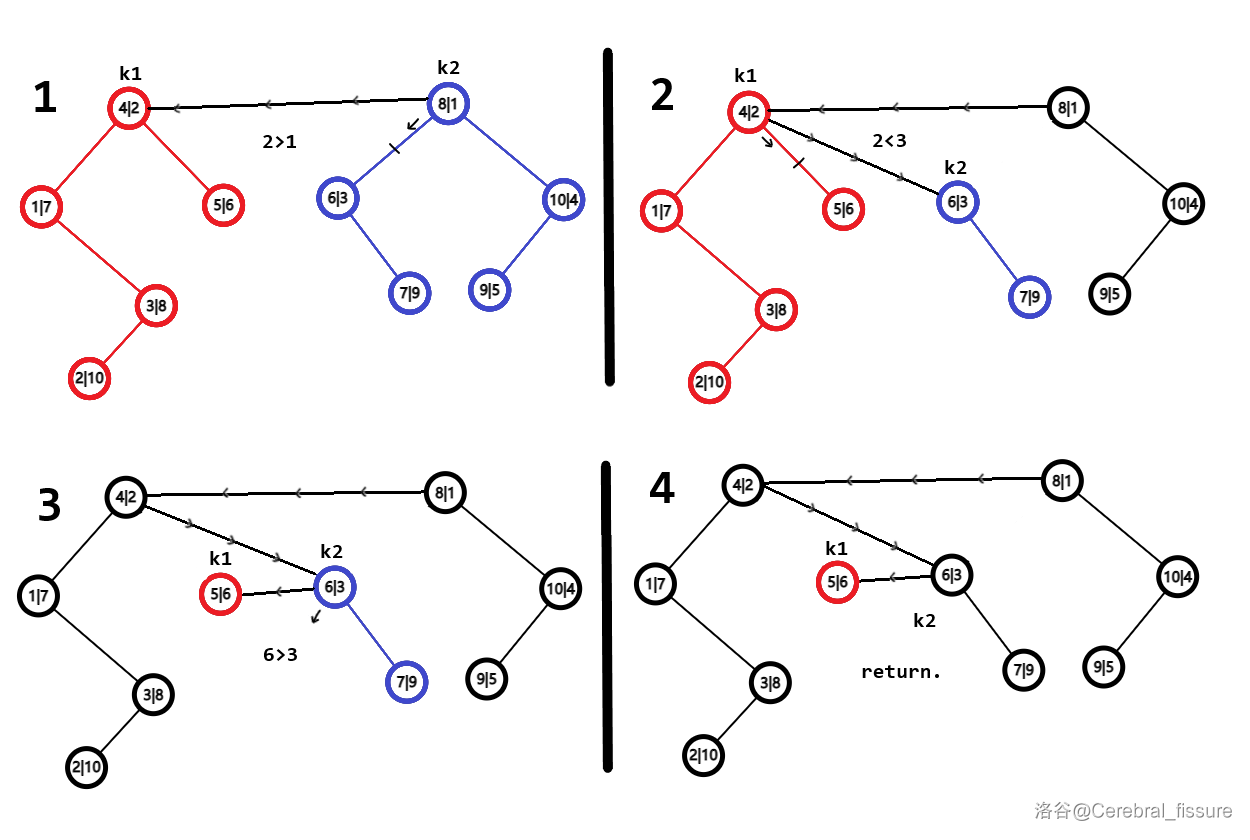
如此操作,即可还原出整棵树。需要注意,如果其中一棵树是空的(\(k=0\)),直接返回另一棵即可。
结果如下。

思路写成代码比较简单。
int merge(int k1,int k2){//把以k1为根的树和k2为根的树缝合在一起
if(k1==0||k2==0){//如果有一个树不存在,返回另一个即可
return k1==0?k2:k1;
}
if(t[k1].val>t[k2].val){//保证树k1中的所有值都小于等于树k2中的值
swap(k1,k2);
}
if(t[k1].key<t[k2].key){//根k1的键小于根k2,树k2应该整个放在k1的右子树里面
t[k1].rc=merge(t[k1].rc,k2);//递归处理
update(k1);//更新size
return k1;//返回根为t1
}else{//否则树k1应该放在k2的左子树里
t[k2].lc=merge(t[k2].lc,k1);
update(k2);
return k2;
}
}
有了Split和Merge,我们就可以开始对Treap大肆蹂躏,完成一些功能了。
插入
为了插入\(x\),我们把树拆成\(\leq x\),\(>x\)的两棵,建立一个值为\(x\)的新节点,把结点和\(\leq x\)的合并,整个再和\(>x\)的合并即可。
struct FHQ_Treap{
void init(int x){//节点初始化,值为x
key=rand();
val=x;
lc=0;
rc=0;
size=1;
}
}
void insert(int x){//插入一个x
ptr++;
t[ptr].init(x);//先建好一个节点
S tmp=split(x,root);//把树分为<=x,>x两部分
root=merge(merge(tmp.Lroot,ptr),tmp.Rroot);//先把<=x和x缝一起,再整个和>x缝一起即可
//这里,有可能root会变。
}
删除
把\(\leq x\)的树拆出来,再从里面把\(\leq x-1\)(也就是\(<x\))的树拿走,剩下的就是全部\(=x\)的树。把根节点的两个儿子互相合并,就会得到一个全新的根。原来的根就被抛弃了,相当于删除。这个操作很巧妙。
void delete(int x){//删除一个x
S tmp1=split(x,root);
S tmp2=split(x-1,tmp1.Lroot);
int Lroot=tmp2.Lroot,Rroot=tmp1.Rroot,mid=tmp2.Rroot;//把树拆成三部分,<x,>x,=x。
root=merge(merge(Lroot,merge(t[mid].lc,t[mid].rc)),Rroot);//把=x的根的两个子树缝在一起,产生了新根,老的就废了
//然后再把三部分缝回去
}
查询排名
把\(\leq x-1\)(\(<x\))的子树拆出来,答案就是\(\leq x-1\)的树的大小+1。所以,需要在插入删除的时候维护大小(使用update())。
void update(int k){//更新节点size
t[k].size=(t[k].lc==0?0:t[t[k].lc].size)+(t[k].rc==0?0:t[t[k].rc].size)+1;
}
int rank(int x){//查询x的排名
S tmp=split(x-1,root);//把<x的子树拆出来
int ans=t[tmp.Lroot].size;//答案就是子树的size+1,但是因为初始化的时候额外加了一个不应该出现的-INF,所以+1抵消了。
root=merge(tmp.Lroot,tmp.Rroot);//缝回去
return ans;
}
这里为什么+1抵消了后面会解释。
查询排名对应的数
使用正常BST的方法即可。
int num(int x){//查询排名为x的数
x++;//有一个不该出现的-INF
int k=root;
while(true){//同正常Treap的思路,从根递归即可。
if(x-t[t[k].lc].size==1){//如果x就是左子树的大小+1,则这个数就是k的值
return t[k].val;
}
if(x-t[t[k].lc].size<1){//如果小于1,这个数在其左子树中。
k=t[k].lc;
}else{//否则在右子树中
x-=t[t[k].lc].size+1;//在右子树中的排名需要减掉左子树的大小+1(k本身也需要减掉一个)
k=t[k].rc;
}
}
return 114514;
}
查询前驱
把\(<x\)的子树拆开,一路往右走找最大值就可以。
int pre(int x){//前驱
S tmp=split(x-1,root);//把<x的子树拆出来,找到子树中的最大值即可
int k=tmp.Lroot;
while(t[k].rc!=0){//一直往右边跳
k=t[k].rc;
}
int ans=t[k].val;
root=merge(tmp.Lroot,tmp.Rroot);
return ans;
}
查询后继
类似,把\(>x\)的子树拆出来往左找最小值。
int suf(int x){//后继,一个套路
S tmp=split(x,root);
int k=tmp.Rroot;
while(t[k].lc!=0&&t[k].lc!=1){//注意这里,后继不能是-INF,所以k不能是1
k=t[k].lc;
}
int ans=t[k].val;
root=merge(tmp.Lroot,tmp.Rroot);
return ans;
}
注意事项
一开始树是空的,什么也没有,没有办法进行任何操作。我们添加一个不该出现的结点,设其的值为-INF(永远会在BST最左边,方便处理),键为INF(除非树空,否则不会是根节点。如果是根节点,查询后继会挂。)
后置废话
对于普通平衡树,输入的值有可能是负的,注意一下。
对于普通平衡树(数据加强版),最大结点数是\(10^6\),空间要开足。因为题目强制O2,所以RE有可能是函数没有返回值。
加上主函数什么的以后,代码总长为2.45KB,相比于我的Treap 5.19KB,Splay 4.09KB,优势明显。(Treap和Splay都是远古时期写的,马蜂废话且抽象)
开O2 478ms(普通平衡树),相比之下Treap只要185ms。可能是因为核心操作全部由递归完成导致常数很大。当然可以给做成非递归的样子缩常数,但是又违背了“好想好写”的特点。
标签:tmp,lc,leq,int,Treap,FHQ,节点 From: https://www.cnblogs.com/CerebralFissure/p/FHQ-Treap.html