「学习笔记」自动机家族

OI 中所说的「自动机」一般都指「确定有限状态自动机」。

一个 确定有限状态自动机（DFA） 由以下五部分构成：

字符集（\(\Sigma\)），该自动机只能输入这些字符。
状态集合（\(Q\)）。如果把一个 DFA 看成一张有向图，那么 DFA 中的状态就相当于图上的顶点。
起始状态（\(start\)），\(start\in Q\)，是一个特殊的状态。起始状态一般用 \(s\) 表示，为了避免混淆，本文中使用 \(start\)。
接受状态集合（\(F\)），\(F\subseteq Q\)，是一组特殊的状态。
转移函数（\(\delta\)），\(\delta\) 是一个接受两个参数返回一个值的函数，其中第一个参数和返回值都是一个状态，第二个参数是字符集中的一个字符。如果把一个 DFA 看成一张有向图，那么 DFA 中的转移函数就相当于顶点间的边，而每条边上都有一个字符。
DFA 的作用就是识别字符串，一个自动机 A，若它能识别（接受）字符串 \(S\)，那么 \(A(S)=\mathrm{True}\)，否则 \(A(S)=\mathrm{False}\)。

当一个 DFA 读入一个字符串时，从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态，那么我们称这个 DFA 接受 这个字符串，反之我们称这个 DFA 不接受 这个字符串。

如果一个状态 \(v\) 没有字符 \(c\) 的转移，那么我们令 \(\delta(v,c)=\mathrm{null}\)，而 \(\mathrm{null}\) 只能转移到 \(\mathrm{null}\)，且 \(\mathrm{null}\) 不属于接受状态集合。无法转移到任何一个接受状态的状态都可以视作 \(\mathrm{null}\)，或者说，\(\mathrm{null}\) 代指所有无法转移到任何一个接受状态的状态。

我们扩展定义转移函数 \(\delta\)，令其第二个参数可以接收一个字符串：\(\delta(v,s)=\delta(\delta(v,s[1]),s[2..|s|])\)，扩展后的转移函数就可以表示从一个状态起接收一个字符串后转移到的状态。那么，\(A(s)=[\delta(start,s)\in F]\)。

如，一个接受且仅接受字符串 a, ab, aac 的 DFA：

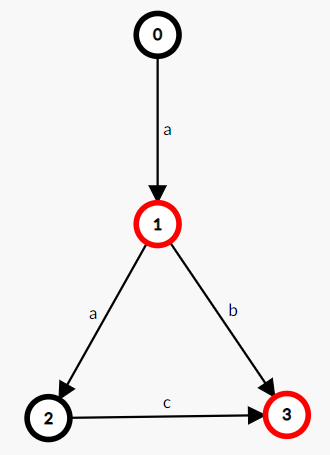
看不懂没关系我也看不懂，不影响你学东西！

OI 中常用的自动机

字典树

「学习笔记」字典树(Trie) - yi_fan0305 - 博客园 (cnblogs.com)

AC 自动机

正在学习

未完待续。。。