题目链接:P4967 黑暗打击
题意
对于 \(n\) 阶的 \(\mathsf{Hilbert}\) 曲线,从上往下灌水,能淹没几个单位面积?
这是 \(1 \sim 4\) 阶的 \(\mathsf{Hilbert}\) 曲线:
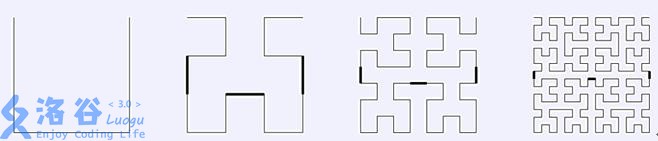
\(h_1\),如最左图所示,是一个缺上口的正方形,这个正方形的边长为 \(1\)。 从\(h_2\) 开始,按照以下方法构造曲线 \(h_i\): 将 \(h_{i-1}\) 复制四份,按 \(2\times2\) 摆放。
把左上一份逆时针转 \(90^{\circ }\),右上一份顺时针转 \(90^{\circ }\),然后用三条单位线段将四分曲线按照左上-左下-右下-右上的顺序连接起来。如图所示,分别展示的是 \(h_2\),\(h_3\),\(h_4\)。加粗的线段是额外用于连接的线段。
注,此题要求对 \(9223372036854775783\) 取模。
\(n \leqslant 10^{10000}\)
Solution
通过观察法,可得以下式子:
\[\begin{cases} f_n = 2f_{n - 1} + 2g_{n - 1} + 3s_{n - 1} + 1\\ g_n = f_{n - 1} + 2g_{n - 1} + s_{n - 1}\\ s_n = 2s_{n - 1} + 1\\ \end{cases}\]其中, \(f_n\) 即为所求, \(g_n\)为旋转90°后可以进水的面积, \(s_n\) 为图形的边长。
写出转移矩阵,则有:
\[\begin{bmatrix} f_{n-1} & g_{n-1} & s_{n-1} & 1 \end{bmatrix} · \begin{bmatrix} 2 & 1 & 0 & 0 \\ 2 & 2 & 0 & 0 \\ 3 & 1 & 2 & 0 \\ 1 & 0 & 1 & 1 \\ \end{bmatrix} = \begin{bmatrix} f_{n} & g_{n} & s_{n} & 1 \end{bmatrix} \]考虑使用矩阵快速幂进行转移,发现 \(n \leqslant 10^{10000}\) , 在规定的时间范围内无法转移。
考虑到线性代数中,矩阵的幂可以转化成对角矩阵求特征值,然后再转换成分别求幂,这种方法可以基于欧拉定理来实现,不妨猜想在矩阵中也可以如此操作。
然而事实上并不是所有的矩阵都可以如此操作,对矩阵对角化后的性质有一定要求,同时跟二次剩余等数论知识有关,不太现实。
对于该种方法不能实现的情况下,参照P4000 斐波那契数列,猜想循环节再加以计算,但是后者时间复杂度较高。
但是起码这道题可以通过欧拉定理来实现快速求解。
但是还是被卡常了,可以对原有公式化简或者使用__int128代替龟速乘解决。
Code
点击查看代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <random>
#include <unordered_map>
using namespace std;
typedef long long lld;
const int N = 1e4 + 50;
const lld mod = 9223372036854775783;
inline int read() {
register int w = 0, f = 1;
register char c = getchar();
while (c > '9' || c < '0') {
if (c == '-') f = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
w = w * 10 + c - '0';
c = getchar();
}
return w * f;
}
inline lld add(register lld a, register lld b) {
a += b;
if (a > mod) a -= mod;
return a;
}
inline lld mul(register lld a, register lld b) {
register lld ans = 0;
while (b) {
if (b & 1ll) ans = add(ans, a);
a = add(a, a);
b >>= 1ll;
}
return ans;
}
struct Mat {
int n, m;
lld dat[5][5];
Mat () {
memset(dat, 0, sizeof (dat));
}
lld * operator [] (register int x) {
return dat[x];
}
inline void init() {
for (register int i = 1; i <= n; ++i)
dat[i][i] = 1;
}
};
Mat operator * (register Mat a, register Mat b) {
register Mat c;
c.n = a.n, c.m = b.m;
for (register int i = 1; i <= c.n; ++i)
for (register int j = 1; j <= c.m; ++j)
for (register int k = 1; k <= a.m; ++k)
c[i][j] = (c[i][j] + mul(a[i][k], b[k][j])) % mod;
return c;
}
inline Mat qpow(register Mat a, lld b) {
Mat base;
base.n = base.m = 4;
base.init();
while (b) {
if (b & 1ll) base = base * a;
a = a * a;
b >>= 1;
}
return base;
}
Mat G, T;
char s[N];
int main() {
scanf("%s", s + 1);
G.n = 1, G.m = 4;
G[1][1] = G[1][3] = G[1][4] = 1;
T.n = T.m = 4;
T[1][1] = 2, T[1][2] = 1;
T[2][1] = 2, T[2][2] = 2;
T[3][1] = 3, T[3][2] = 1, T[3][3] = 2;
T[4][1] = T[4][3] = T[4][4] = 1;
register lld sum = 0;
for (register int i = 1; s[i]; i++)
sum = (sum * 10 + s[i] - '0') % (mod - 1);
sum = (sum - 1 + mod) % mod;
T = qpow(T, sum);
G = G * T;
printf("%lld\n", G[1][1]);
return 0;
}