标签：frac ad sum 复杂度 一个点 矩形 合集 边权 hoc

APC001F

题目链接

一眼不可做，直接对边权处理是没有思路的。于是考虑边权转点权。

令 \(val_u\) 表示所有与 \(u\) 相连的边边权的异或和。

考虑现在对链的异或操作变为了什么，设当前对链 \(u\rightarrow v\) 异或上值 \(p\) ，对链上一个点 \(x\)，我们分两种情况讨论。

• \(x=u/v\)，此时 \(val_x=val_x\oplus p\)
• \(x\neq u/v\)，此时 \(val_x=val_x\oplus p\oplus p=val_x\)

所以每次对链的操作转化为了对两个点操作，此时边权为 \(0\) 等价于所有点权为 \(0\)。

不难想到每次最多只会让两个点的值变 \(0\) ，所以最优策略一定是优先找到两个相同的数，使其异或上自己。所以，每种数字最后只留下不超过一种。

而 \(a_i\leq 15\)，于是可以考虑子集 dp。设 \(f[S]\) 表示让集合 \(S\) 内的数都为 \(0\) 的最小步数，则转移为 \(f[S]=f[S']+f[S\oplus S']\)，其中 \(S'\) 为 \(S\) 的子集。时间复杂度 \(O(3^{16})\)。

AGC018E

题目链接

三个矩形乱跑显然难搞，那就一点点推吧。

1. 从一个点到另一个点

不妨令一个点的坐标为 \((0,0)\)，另一个点相对坐标为 \((x_1,y_1)\)，方案数即为 \(\binom{x_1+y_1}{x_1}\)。

2. 从一个点到一个矩形

首先考虑暴力咋搞，令 \(f((a,b)\rightarrow (p,q))\) 为从 \((a,b)\) 到 \((p,q)\) 的方案数。

\[\sum_{x=x_1}^{x_2}\sum_{y=y_1}^{y_2} f((0,0)\rightarrow(x,y)) \]

而矩形是可以被拆分成四个 \(\text{2-side}\) 矩形的，具体的说，我们记 \(g(x,y)\) 为走到 \((x,y)\) 的 \(\text{2-side}\) 矩形的方案数，则答案可表示为

\[g(x_2,y_2)-g(x_2,y_1-1)-g(x_1-1,y_2)+g(x_1-1,y_1-1) \]

然后考虑快速计算 \(g\)。砸个表上去。

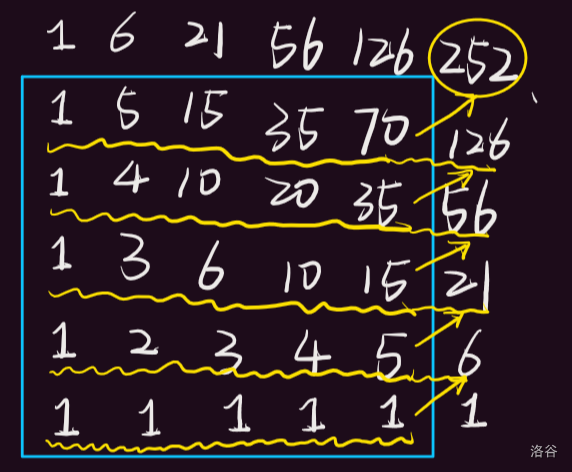
然后你就发现 \(g(x,y)=f(x+1,y+1)-1\)

所以答案变为

\[f(x_2+1,y_2+1)-f(x_2+1,y_1)-f(x_1,y_2+1)+f(x_1,y_1) \]

加一减一消去了，所以是上边的形式。

这让一个矩形转变成了四个点

3. 从一个矩形到一个矩形

先大力写出暴力式子。

\[\sum_{x'=x_1'}^{x_2'}\sum_{y'=y_1'}^{y_2'} \sum_{x=x_1}^{x_2}\sum_{y=y_1}^{y_2} f((x',y')\rightarrow(x,y)) \]

然后用上文中的式子去掉两重循环

\[\sum_{x'=x_1'}^{x_2'}\sum_{y'=y_1'}^{y_2'} f((0,0)\rightarrow(x_2+1-x',y_2+1-y'))+... \]

在这里只写出一个结果。注意到从一个矩形到点和一个点到矩形的方案数是显然等价的，所以进一步写为

\[\sum_{x'=x_1'}^{x_2'}\sum_{y'=y_1'}^{y_2'} f((0,0)\rightarrow(x'-x_2-1,y'-y_2-1))+... \]

然后注意到上文在拆分求和以后依然是四个点到矩形的形式，依然可以套用上式化简。最后能把两个矩形都转化为四个点，做 \(4\times 4\) 次枚举后套用公式即可。

4. 从一个矩形经过一个矩形到一个矩形

由于上文中所述的矩形转点思想（姑且这么说吧 qwq），我们只需要考虑一个点经过一个矩形到另一个点的方案数即可。

整个过程可以拆分为两部分

• 从起点到第二个矩形的边界
• 从第二个矩形的边界到下一个点

由于要求最短路径，所以进入矩形的边界一定是下/左边界。枚举下边界和左边界上的点，然后再跑一次点到点即可。

5. 从一个矩形经过一个矩形到一个矩形的路径长度之和

终于到了本题要干的事情了。

考虑在 4 上做一些修改，把整个过程拆成三部分

• 从起点到第二个矩形的边界
• 从第二个矩形的下/左边界到第二个矩形的上/右边界
• 从第二个矩形的边界到下一个点

观察从第二个矩形的边界跑到第二个矩形的边界这一过程，假设我们知道当前的两个点是 \((x_1,y_1)\) 和 \((x_2,y_2)\)，那么对答案的贡献便是 \(f((x_1,y_1)\rightarrow(x_2,y_2))\times (x_2-x_1+y_2-y_1)\) 这个可以拆成两部分计算。枚举左右上下边界上的点，跑一遍上文中的计算方式，但是要注意符号问题，同样的问题出现在 2,3,4 中。时间复杂度 \(O(n)\)，\(n\) 为值域。

CF1707E

题目链接

第一道 3500。

下文中，我们称调用 \(k\) 次题面中所述的 \(f\) 函数后所得的区间为 \(f^k(l,r)\)，下文中所述的对二元组 \((l_1,r_1),(l_2,r_2)\) 进行的加法操作后得到的结果为 \((\min(l_1,l_2),\max(r_1,r_2))\)，二元组中的两个元素分别为 \(l,r\)，\(p(l)\) 表示 \(p\) 这个二元组中的元素 \(l\)。

首先看到这种一眼不可做的题先猜性质 qwq。

注意到每次操作区间带有可拆分的性质。即

\[f^k(l,r)=f^k(l,l+1)+f^k(l+1,l+2)+\ ...\ +f^k(r-1,r) \]

如何证明？考虑归纳。

首先 \(k=0\) 时显然成立。

当 \(k=1\) 时，我们设最小值\(mn\) 出现在位置 \(x\)，最大值 \(mx\) 出现在位置 \(y\)，则 \(f(x-1,x)(l)=f(x,x+1)(l)=mn\)，\(f(y-1,y)(r)=f(y,y+1)(r)=mx\)。显然每两个二元组中一定有一个存在于右式中，故左右答案相等。

同理可推广到高次情况。

现在咋做呢？

我们设 \(g^k(x)\) 表示 \(f^k(x,x+1)\)，那么答案一定是找到最小的 \(k\) 使得 \(g^k(x)=(1,n)\)，而 \(f^k(1,n)=(1,n)\)（如果此时 \(a\) 中存在 \(1\) 和 \(n\)，否则除非询问二元组是 \((1,n)\)，经过任意次变换都不可能是 \((1,n)\)），所以可以倍增做，预处理出所有 \(k=2^i\) 时 \(g^k(x)\) 的值，询问时转化为对于是否二元组 \((l,r)\) 调用 \(2^k\) 次使得二元组不是 \((1,n)\)，即 \(g^{2^k}(l)+g^{2^k}(l+1)+\ ...\ +g^{2^k}(r-1)\neq (1,n)\)，答案即为次数加 \(1\)。而上边的加法操作是可以 st 表维护的。

问题转化为如何快速求 \(g\)，\(g^{2^k}(x)=g^{2^{(k-1)}}(g^{2^{(k-1)}}(x))\)，而 \(g^{2^{(k-1)}}(x)\) 是已知的，令其为 \((l,r)\)，问题又变为询问 \(g^{2^k}(x)=g^{2^{(k-1)}}((l,r))\)，仿照上文的询问 st 表维护即可。

时间复杂度 \(O(n\log^2n)\)

P6982

题目链接

首先发现 \(\frac{n}{2}\) 是最奇怪的，考虑从这里入手。

假设我们知道了一个返回值为 \(\frac{n}{2}\) 的串，那么我们可以在 \(n\) 次操作后得到原串。具体做法如下。

首先取反第一位，然后对剩下的第 \(2,3,...,n\) 位按位取反。分情况讨论

• 返回值为 \(\frac{n}{2}\)，说明该位正确性与第一位不同。
• 返回值为 \(0\)，说明该位正确性与第一位相同。

在你得到了所有位与第一位的正确性关系后，将所有正确性不同的取反，做一次询问，返回值为 \(n\) 即为原串，否则为反串。

接下来考虑如何得到一个返回值为 \(\frac{n}{2}\) 的串。

大力随机！

考虑正确性，也就是说，我们要从 \(n\) 个位置中取出恰好 \(\frac{n}{2}\) 个位置使得该位与原串相同，剩下的不同，那一次成功的概率即为 \(\frac{\binom{\frac{n}{2}}{n}}{2^n}\)。那么在 \(500\) 次内问不出来的概率为 \((1-\frac{\binom{\frac{n}{2}}{n}}{2^n})^{500}\)。这个东西不会很大，因为 \(\binom{\frac{n}{2}}{n}\leq2^{n-1}\)。所以直接随机询问即可。

P5101

题目链接

首先题面对折叠给了个非常反人类的定义，这里来简化一下

• 选择一个左端点是原串左端点的长度为偶数的回文串，保留其右半部分。
• 选择一个右端点是原串右端点的长度为偶数的回文串，保留其左半部分并将其放到开头，然后将原串其余部分翻转后接在其后边。

并且由于厚度，染色操作必然在翻折前进行。

有一个显然的性质是，一个串最后能被缩到长度为 \(2\) 的串，其中的颜色必然不超过 \(2\) 个（因为翻折操作不会减少颜色种类数）。

考虑进一步推广，一个串能被缩短到长度为 \(2\) 的串，需要其除首位外每个连续段长度均为偶数，充分性是显然的，必要性证明如下。

若存在一个连续段长度为奇数且不在首位，则将其两端缩起来后，必定为 \(x...x,y...y,x...x\) 其中 \(y\) 有奇数个，此时两端的 \(x\) 无法翻折到一起，长度至少为 \(3\)。

又注意到每个长度为偶数的连续段可以拆成若干个长度为 \(2\) 的连续段，为奇数的同理可拆出若干个长度为 \(2\) 的连续段+一个单独颜色，考虑对原序列进行划分处理。去除首尾的限制则可以通过枚举起始点解决。

接下来对每个小段进行考虑，我们钦定 \(c\) 为当前考虑的颜色

• 如果小段内都为 \(c\)，不更改。
• 如果小段内其中一个颜色为 \(c\)，将另一根线也改为 \(c\) 不劣。
• 如果小段的颜色都不为 \(c\)，则需要根据另一种颜色来决定更改。

设对于颜色 \(c\) 答案为 \(ans_c\)，则有 \(ans_c=\min_{c'}(n-cnt_c-cnt_{c'}-cost_{c,c'})\)，其中 \(cnt_i\) 为颜色 \(i\) 出现次数，\(cost_{c_1,c_2}\) 表示使用 \(c_1,c_2\) 的最小花费，\(c'\) 为另一种颜色，其实 \(cost_{c_1,c_2}\) 就是包括 \(c_1,c_2\) 两种颜色的小段数量。

暴力枚举做到 \(O(nm^2)\)。

枚举每个包括 \(i\) 的小段，开桶维护 \(cnt_{c'}\) 根据上文所述进行更改即可做到均摊 \(O(n)\)。

ABC235Ex

题目链接

由于我们无法定义点集，我们不妨建立一个集合和整数的函数关系 \(g\)，\(g(S)=x\) 表示 \(x\) 是 \(S\) 被构建的最小次数。这里的 \(S\) 与上文意义相同。不妨考虑定义一个多项式 \(f(G)\)，\([x^i]f(G)\) 表示在图 \(G\) 中，\(g(S)=i\) 的 \(S\) 数量，其中 \([x^i]F\) 表示在多项式 \(F\) 中，\(i\) 次项的系数。不难发现每个 \(S\) 唯一对应一个 \(x\)，因此答案即为 \(\sum\limits_{i=0}^k[x^i]f(G)\)，其中 \(G\) 为给定的图。在这里，对于两个不连通的子图 \(G_1\)，\(G_2\)，两个多项式 \(f(G_1),f(G_2)\) 相乘的意义是 \(f(G)\)，\(G\) 是将 \(G_1\) 和 \(G_2\) 合并后的图。

不妨简化条件，首先设原图是一个树，且边权互不相同。

我们将边权排序并从小到大考虑每条边，对于当前边 \(e\)，设其连接的两个连通块分别为 \(T_1,T_2\)，连接后的连通块为 \(T\)，我们进行分类讨论：

• 我们让所有对 \(T\) 进行的操作选择的 \(x\) 都小于 \(e\) 的边权：这意味着两个连通块进行的操作是独立的，故答案为 \(f(T_1)*f(T_2)\)

• 存在一个操作选择了一个不小于 \(e\) 的边权 \(x\)：这意味着两个连通块必定被染红。

因此，我们将其这两个多项式合并的答案为 \(f(T_1)*f(T_2)-x^2+x\)。也就是说，使得两个点集完全变成红色由之前的至少两次变为了至少一次。

到这一步我们其实也看出了为什么要让边权互不相同，如果存在相同边权，那么选择不小于 \(e\) 的边权后合并的连通块个数将不确定。

不妨设对于一个连通块 \(T\)，考虑到所有边权为 \(x\) 的边时其多连通的所有连通块为 \(T_1,T_2,...,T_m\)，则答案为 \(\prod\limits_{i=1}^mf(T_i)-x^m+x\)。

最后使原图不是树，我们将证明，\(f(\text{MST}(G))\) 的答案和 \(f(G)\) 的答案相同。\(\text{MST}(G)\) 表示 \(G\) 的最小生成树。

设一条不在最小生成树上的边 \(e\)，由于最小生成树的基环性质，则在其两端点的路径上任取一点 \(u\) 并进行一次 \(u,w(e)\) 的操作与有无 \(e\) 都是等价的。故答案不变。

由于一共合并 \(O(n)\) 次，单次合并复杂度为多项式乘法的 \(O(k^2)\)，故总复杂度看起来是 \(O(nk^2)\) 的。

官方说复杂度可以证明是 \(O(nk)\) 的，但是我不会证，这里给出我的 \(O(nk\log n)\) 理解。

考虑构造一个复杂度的上界，对于合并为大小为 \(S\) 的连通块，其最坏复杂度是 \(O(\dfrac{S^2}{4})\) 的。

所以最坏的合并方案是一直合并两个大小相同的点集。将会发生 \(\dfrac{n}{2}\) 次大小为 \(1\) 的合并，\(\dfrac{n}{4}\) 次大小为 \(2\) 的合并，\(\dfrac{n}{2^{i+1}}\) 次大小为 \(2^i\) 的合并。单次的复杂度为 \(O(n2^i)\)，而 \(2^i\leq k\)，故总复杂度上界为 \(O(nk\log n)\)。

标签：frac,ad,sum,复杂度,一个点,矩形,合集,边权,hoc
From： https://www.cnblogs.com/-Complex-/p/17555350.html