CF1846D Rudolph and Christmas Tree 题解

Decription

一颗圣诞树由 \(n\) 个底边为 \(d\)，高度为 \(h\) 的等腰三角形组成，每个三角形以 \(y\) 轴为对称轴，底边均平行于 \(x\) 轴，三角形有可能重叠。

给出 \(n,d,h\) 以及每个三角形底边与 \(x\) 轴的距离,求该圣诞树的面积。

Solution

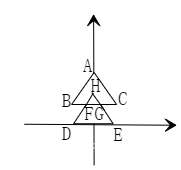
如图，这是一棵圣诞树,其由两部分组成，完整的一个三角形 \(ABC\) 和 等腰梯形 \(DEGF\)（底边之差大于 \(h\) 时,为完整的一个三角形）。

设 \(dd=FG,hh=BD\)。

\(\therefore S_{\texttt{tree}}=S_{\vartriangle \texttt{ABC}}+S_{\texttt{梯DEGF}}=d\times h\div2+(d+dd)\times hh\)

\(\because S_{\vartriangle HFG}\sim S_{\vartriangle HDE}\)

\(\therefore \dfrac{dd}{d}=\dfrac{h-hh}{h}\)

\(\therefore dd=(h-hh)\div h\times d\)

因为 \(hh\) 为两三角形上下底边之差，所以所有数据都已知，可以得出答案。

Code

#include<bits/stdc++.h>
using namespace std;
#define doubl long double
int t;
double a[200200]; //要记得开 double
void solve(){
	int n;
	double d,h,ans=0;
	cin>>n>>d>>h;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=2;i<=n;i++){
		if(a[i]-a[i-1]>h) ans+=d*h/2.0; //不重叠时是一个三角形
		else {
			double dd=(h-(a[i]-a[i-1]))*d/h;
			ans+=(dd+d)*(a[i]-a[i-1])/2.0;  //得出梯形面积
		}
	}
	ans+=d*h/2.0;  //最后一个图形总为完整的三角形
	printf("%.6lf\n",ans); //要输出6位小数
}
int main(){
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}