Solution to Question Ⅰ
首先缩点(当然也可以不缩?),然后跑一遍 DFS 即可。
//w为联通分量里的节点个数
inline void dfs (const int &u) {
ans1[u] = w[u];
for (int v : G_scc[u])
dfs(v), ans1[u] += ans1[v];
}
Solution to Question Ⅱ
观察缩完点后的图一定是保证无环的,又由于题目有个非常特殊的条件:图中有一个中心点 \(r\),对于其它所有点,有且仅有一条路径可达。于是,缩完点后的图一定是一棵以 \(r\) 为根节点的 树。
对于节点 \(u\),它的子树中的节点想要到达其它子树,就必须往上爬,于是有了一个贪心的思路:「每一次连边都需要尽量往上连」。
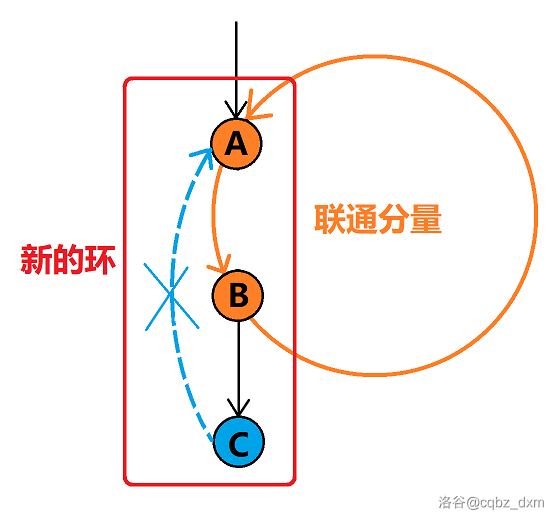
注意这里的到达是指有且仅有一条路径,考虑下图情况:如果我们想从 \(C\) 往 \(A\) 甚至更上面连边,此时由于 \(A,B\) 在同一个联通分量中,\(B\) 原来是可以达到 \(A\) 的,再连上这条边之后,\(B\) 就有 \(2\) 条路径可以到达 \(A\)(\(A,B,C\) 又形成了一个新的环),是不符合题意的。
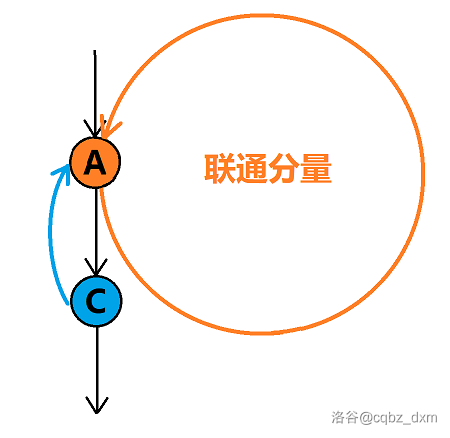
但是对于如下图「特例」,向上连的边,仅是“擦边”经过联通分量。此时这条边是可连的。
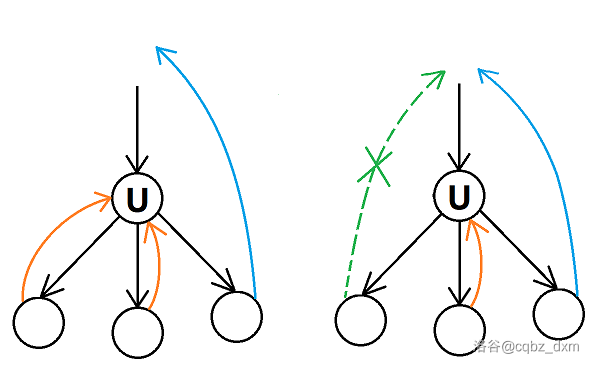
对于节点 \(u\),它的子节点有如下两种情况:(下图均为缩完点后的图)
-
所有节点都连接到 \(u\),再由 \(u\) 连一条边向上。

-
有且 仅有一条 边直接跳过 \(u\),直接向上连边,且满足「特例」(见上)。
「仅有一条」:因为如果有第二条边向上连,则会有两个环经过同一条路径(\(u\) 往上)。
实现
由于缩完点是一棵树,考虑用 \(edge[]\) 记录下每个节点往上的那条边起始点在原图中的编号。
建图时,加上:
edge[scc[v]] = make_pair(u, v),
这样我们可以在 \(O(1)\) 的时间复杂度,判断相邻的三个连通分量 \(A,B,C\),是否只经过位于中间的连通分量 \(B\) 中的一个点。
edge[B].second == edge[C].first
Summary
- 这道题需要考虑很多情况;
- 实现起来也还是有点难度。