首页 > 其他分享 >二分图学习笔记

二分图学习笔记

时间：2023-07-12 20:35:27浏览次数：55  
标签：二分 匹配 int cap 笔记 学习 dep add define

定义

对于一个无向图 \(G=(V,E)\)，如果存在点集 \(A,B\)，满足 \(a\neq\varnothing\)，\(b\neq\varnothing\)，\(A\cap B=\varnothing\)，\(A\cup B=V\)，且 \(\forall u,v\in A\) 或 \(u,v\in B\)，都有 \((u,v)\notin E\)，则称这个图是一个二分图，\(A\) 称为这个二分图的左部，\(B\) 称为右部。

一个二分图可以记作 \(G=(A,B,E)\)，下文中使用这种记法时，默认 \(|A|\le|B|\)。

判定

一个图是二分图 \(\iff\) 图中没有奇环。

可以用 DFS 染色 或 扩展域并查集 判断。

例题：

二分图最大匹配

定义

  • 对于一个图 \(G=(V,E)\)，如果一个边集 \(S\subseteq E\) 满足其中任意两条不同的边没有公共端点，则称 \(S\) 为图 \(G\) 的一个匹配。

  • 对于匹配 \(S\)，属于 \(S\) 的边叫做匹配边，不属于 \(S\) 的边叫做非匹配边。

  • 如果点 \(u\) 是一条匹配边的端点，则称 \(u\) 为匹配点，否则是非匹配点。

    匹配边的两端都是匹配点；非匹配边的两端要么都是匹配点，要么一个是匹配点，一个是非匹配点。

  • 对于二分图 \(G=(A,B,E)\)，如果它的一个匹配 \(S\) 满足 \(A\) 中所有点都是匹配点，则称 \(S\) 为 \(G\) 的一个完美匹配。

求解

二分图最大匹配问题可以用网络流求解。建立超级源点 \(S\) 和超级汇点 \(T\)，原图中每条边从左部连向右部，容量为 \(1\)，从 \(S\) 向每个左部点连一条容量为 \(1\) 的边，从每个右部点向 \(T\) 连一条容量为 \(1\) 的边，新图的最大流就是最大匹配，其中匹配边流量为 \(1\)，非匹配边流量为 \(0\)。

在单位容量的网络中，使用 Dinic 的时间复杂度为 \(O(m\sqrt n)\)。

我太菜了，不会匈牙利算法。

模板代码：（Luogu P3386 【模板】二分图最大匹配）

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
// #define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 1005, M = 2e5 + 5;
int n, m, e, t;
int hd[N], to[M], nxt[M], cap[M], tot = 1;
int dep[N], cur[N];
void add(int u, int v, int w) {
    to[++tot] = v;
    cap[tot] = w;
    nxt[tot] = hd[u];
    hd[u] = tot;
}
bool bfs() {
    memset(dep, 0, sizeof dep);
    queue<int> q;
    q.push(0);
    dep[0] = 1;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i = hd[u]; i; i = nxt[i]) 
            if(cap[i] && !dep[to[i]])
                dep[to[i]] = dep[u] + 1, q.push(to[i]);
    }
    return dep[t];
}
int dfs(int u, int flow) {
    if(u == t) return flow;
    int res = 0;
    for(int i = cur[u]; i && flow; i = nxt[i]) {
        cur[u] = i;
        if(dep[to[i]] == dep[u] + 1) {
            int o = dfs(to[i], min(cap[i], flow));
            flow -= o;
            res += o;
            cap[i] -= o;
            cap[i ^ 1] += o;
        }
    }
    return res;
}
int dinic() {
    int ans = 0;
    while(bfs()) {
        rep(i, 0, t) cur[i] = hd[i];
        ans += dfs(0, INT_MAX);
    }
    return ans;
}
signed main() {
#ifdef ONLINE_JUDGE
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
#endif
    cin >> n >> m >> e;
    t = n + m + 1;
    rep(i, 1, e) {
        int u, v; cin >> u >> v;
        v += n;
        add(u, v, 1), add(v, u, 0);
    }
    rep(i, 1, n) add(0, i, 1), add(i, 0, 0);
    rep(i, 1, m) add(i + n, t, 1), add(t, i + n, 0);
    cout << dinic() << endl;
    return 0;
}

常见模型

最小路径覆盖

对于一个有向无环图 \(G=(V,E)\)，如果存在一个简单路径的集合 \(S\)，满足 \(V\) 中的每个点都恰好在 \(S\) 中的一条路径上，则称 \(S\) 为 \(G\) 的一个路径覆盖。求出所含路径条数最少的路径覆盖。

首先每个点单独构成一条路径肯定是一组路径覆盖。考虑通过图中的边合并这些路径使它变小。

将每个点 \(u\) 拆成两个点 \(u_{in}\) 和 \(u_{out}\)，对于原图中的每一条边 \((u,v)\)，在新图中连接 \((u_{out},v_{in})\)。在路径覆盖中，每个点最多只有 \(1\) 条入边和 \(1\) 条出边，这对应着新图中的每个点最多只被一条边选中，因此求出新图的最大匹配 \(P\)，每选择一条边代表合并了一次路径，最小路径覆盖的大小即为 \(|V|-P\)。每条匹配边对应路径覆盖中的一条边，因此也容易构造出最小路径覆盖。

代码：（Luogu P2764 最小路径覆盖问题）

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
// #define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 205, M = 6005;
int n, m, t;
int to[M * 4], nxt[M * 4], cap[M * 4], hd[N * 2], tot = 1;
int cur[N * 2], dep[N * 2]; 
int fr[N];
void add(int u, int v, int w) {
    to[++tot] = v;
    cap[tot] = w;
    nxt[tot] = hd[u];
    hd[u] = tot;
}
bool bfs() {
    memset(dep, 0, sizeof dep);
    dep[0] = 1;
    queue<int> q;
    q.push(0);
    while(!q.empty()) {
        int u = q.front();
        cur[u] = hd[u];
        q.pop();
        for(int i = hd[u]; i; i = nxt[i]) {
            int v = to[i];
            if(cap[i] && !dep[v]) 
                dep[v] = dep[u] + 1, q.push(v);
        }
    }
    return dep[t];
}
int dfs(int u, int flow) {
    if(u == t) return flow;
    int res = 0;
    for(int i = cur[u]; i && flow; i = nxt[i]) {
        cur[u] = i;
        int v = to[i];
        if(dep[v] == dep[u] + 1) {
            int o = dfs(v, min(flow, cap[i]));
            flow -= o;
            res += o;
            cap[i] -= o;
            cap[i ^ 1] += o;
        }
    }
    return res;
}
int dinic() {
    int ans = 0;
    while(bfs()) ans += dfs(0, INT_MAX);
    return ans;
}
int find(int x) {
    for(int i = hd[x]; i; i = nxt[i]) 
        if(!(i & 1) && !cap[i]) return to[i] - n;
    return 0;
}
signed main() {
#ifdef ONLINE_JUDGE
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
#endif
    cin >> n >> m;
    t = n * 2 + 1;
    rep(i, 1, n) {
        add(0, i, 1), add(i, 0, 0);
        add(i + n, t, 1), add(t, i + n, 0);
    }
    rep(i, 1, m) {
        int u, v; cin >> u >> v;
        add(u, v + n, 1), add(v + n, u, 0);
    }
    int ans = n - dinic();
    rep(i, 1, n) fr[find(i)] = i;
    rep(i, 1, n) if(!fr[i]) {
        cout << i << ' ';
        int o = find(i);
        while(o) {
            cout << o << ' ';
            o = find(o);
        }
        cout << endl;
    }
    cout << ans << endl;
    return 0;
}

最小可重路径覆盖

对于一个有向无环图 \(G=(V,E)\)，如果存在一个简单路径的集合 \(S\)，满足 \(V\) 中的每个点都至少在 \(S\) 中的一条路径上，则称 \(S\) 为 \(G\) 的一个可重路径覆盖。

做传递闭包后转化为不可重路径覆盖。

常用定理

König 定理

对于二分图 \(G=(V,E)\)，设 \(P\) 为其最大匹配的大小，则有最小点覆盖 \(=P\)（点覆盖：一个点集 \(S\subseteq V\)，满足 \(\forall(u,v)\in E\)，都有 \(u\in S\lor v\in S\)。即每条边至少选择一个端点）

  • 证明（含构造方案）：

    • 首先显然有最小点覆盖 \(\ge P\)，因为每条匹配边至少有一个端点被选择。

    • 考虑从右部每个非匹配点开始 DFS，从右往左只能走非匹配边，从左往右只能走匹配边。设 左部被 DFS 到的点 和 右部没被 DFS 到的点 构成的集合为 \(S\)，\(S\) 就是一个最小点覆盖。

    • 首先证明 \(|S|=P\)：

      • 首先注意到每次 DFS 中，除了起点，被 DFS 到的都是匹配点。

      • 因为从左往右只能走匹配边，也就只能走到匹配点。而从右往左虽然只能走非匹配边，但是走不到非匹配点，因为如果走到了非匹配点，就说明发生了以下这种情况：（红色为匹配边）

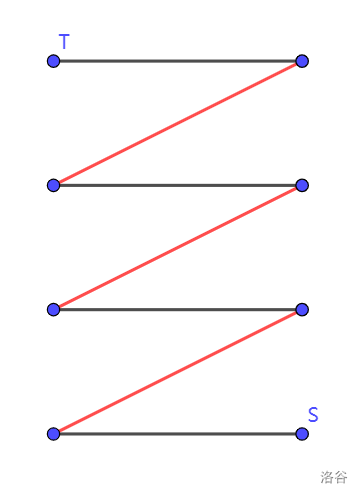
      • 显然这存在更大的匹配，与最大匹配矛盾，因此不可能从右部走到非匹配点。

      • 而右部的非匹配点都作为起点被 DFS 过，没被 DFS 过的只能是匹配点。如果右部的一个匹配点没被 DFS 过，它就会被加入 \(S\)。右部的一个匹配点被 DFS 过，当且仅当其对应的左部匹配点也被 DFS 过，因此这个左部匹配点被加入 \(S\)。这说明对于每条匹配边，都有且仅有一个端点被加入了 \(\boldsymbol S\)。因此 \(|S|=P\)。

    • 然后证明 \(S\) 是一个点覆盖：

      • 上文已经证明匹配边肯定全被覆盖。一条非匹配边没被 \(S\) 覆盖到的充要条件是，左部端点没被 DFS 过 且 右部端点被 DFS 过。
      • 如果一个右部点被 DFS 过，则所有与它相连的非匹配边都被 DFS 过，因此这个条件不可能满足，即不存在未被覆盖的边，所以 \(S\) 是一个点覆盖。

    • 综上，\(S\) 是一个最小点覆盖。

推论：最大独立集 \(=|V|-P\)（独立集：一个点集 \(S\subseteq V\)，满足 \(\forall u,v\in S\)，都有 \((u,v)\notin E\)。即选择的点之间不能有边）

  • 证明：

    • 对于每个独立集 \(S\)，其补集 \(\complement_VS\) 都是一个点覆盖。
    • 所以最大独立集对应最小点覆盖，大小为 \(|V|-P\)。

最小边覆盖

对于二分图 \(G=(V,E)\)，设 \(P\) 为其最大匹配的大小，则有最小边覆盖 \(=|V|-P\)（边覆盖：一个边集 \(S\subseteq E\)，满足 \(\forall u\in V\)，都 \(\exists v\in V,(u,v)\in E\)。即每个点至少选择一条出边）

  • 证明：

    • 一条边加入边覆盖中，可能覆盖了一个或两个未覆盖的点。
    • 要使边覆盖最小，就要让覆盖了两个未覆盖点的边最多。
    • 这种边就是匹配边，向边覆盖中加入每条匹配边，总共覆盖了 \(2P\) 个点。
    • 剩下的点每个点对应一条边，这些边的数量为 \(|V|-2P\)，边覆盖中的总边数就是 \(|V|-2P+P=|V|-P\)。

Hall 定理：

对于二分图 \(G=(A,B,E)\)，定义函数 \(f(S)\) \((S\subseteq A)\) 表示与 \(S\) 中的点有连边的点的数量，则 \(G\) 存在完美匹配的充要条件是 \(\forall S\subseteq A,f(S)\ge|S|\)。

看着很对，证明不会。

Dilworth 定理

对于一个有向无环图 \(G=(V,E)\)，其最长反链的大小等于最小可重路径覆盖的大小。

反链：如果一个点集 \(S\subseteq V\) 满足 \(\forall u,v\in S,u\neq v\)，不存在 \(u\) 到 \(v\) 的路径，则称 \(S\) 为图 \(G\) 的一个反链。

证明不会。

模板题：Luogu P4298 [CTSC2008] 祭祀

给定一个有向无环图 \(G=(V,E)\, (|V|=n,|E|=m)\)，有三问：

  • 求出其最长反链长度。
  • 构造最长反链。
  • 判断每个点是否可能在最长反链中。

\(n\le100,m\le1000\)。

第一问，根据 Dilworth 定理，做出传递闭包，做最小不可重路径覆盖即可。构造的二分图 \(G'=(V_{in},V_{out},E')\) 中的一条边 \((u_{out},v_{in})\in E\) 代表 \(u\) 能到达 \(v\)。

第二问，找出二分图的最大独立集 \(S\)，所有满足 \(u_{in}\in S\land u_{out}\in S\) 的 \(u\) 构成的集合 \(L\) 就是最长反链。最大独立集是最小点覆盖的补集，先求出最小点覆盖再求补集即可，构造方案见上文 König 定理。

因为取出的每个 \(u\) 都满足 \((u_{in},u_{out})\) 都在同一个独立集中，所以这些点也构成独立集，也就是不存在边 \((u_{in},v_{out})\)（代表 \(u\) 能到达 \(v\)），满足反链的定义。

接下来证明这些点构成的反链是最长的：

设 \(P\) 是 \(G'\) 的最大匹配数，显然 \(P\le n\)，\(|S|=|V_{in}|+|V_{out}|-P=2n-P\)。满足在 \(v_{in}\) 和 \(v_{out}\) 中有且仅有一个属于 \(S\) 的节点 \(v\) 最多只有 \(n-|L|\) 个，而每个 \(L\) 中的元素在 \(S\) 中对应两个元素，所以 \(|S|-2|L|\) 就是这样的 \(v\) 的数量，所以 \(|S|-2|L|\le n-|L|\)，移项得到 \(|L|\ge|S|-n\) 即 \(|L|\ge n-P\)，反链最长也只有 \(n-P\)，所以 \(|L|=n-P\)，\(L\) 是最长反链。

第三问，枚举每个点分别判断。考虑强制选中这个点，然后再求最长反链，如果最长反链不变，这个点就可以在最长反链中。具体地，如果选中一个点，那么所有和这个点有偏序关系（路径）的点都不能选，所以将这些点都删掉，对剩下的点求最长反链，如果只减少了 \(1\)，这个点就合法。

时间复杂度：求传递闭包的时间复杂度为 \(O(n^3)\)，求完传递闭包后的边数 \(m'=O(n^2)\)，跑一次二分图匹配的时间复杂度是 \(O(m'\sqrt n)=O(n^{2.5})\)，第三问要枚举每个点分别跑二分图匹配，所以总时间复杂度为 \(O(n^{3.5})\)。

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
// #define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 105, M = 1005;
int n, m, c[N][N];
int to[N * N], nxt[N * N], cap[N * N], hd[N * 2], tot = 1;
int cur[N * 2], dep[N * 2], t;
bool del[N * 2], vis[N * 2];
string s1, s2;
void add(int u, int v, int w) {
    to[++tot] = v;
    cap[tot] = w;
    nxt[tot] = hd[u];
    hd[u] = tot;
}
bool bfs() {
    memset(dep, 0, sizeof dep);
    dep[0] = 1;
    queue<int> q;
    q.emplace(0);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        cur[u] = hd[u];
        for(int i = hd[u]; i; i = nxt[i]) {
            int v = to[i];
            if(cap[i] && !del[v] && !dep[v]) {
                dep[v] = dep[u] + 1;
                q.push(v);
            }
        }
    }
    return dep[t];
}
int dfs(int u, int flow) {
    if(u == t || !flow) return flow;
    int res = 0;
    for(int i = cur[u]; i && flow; i = nxt[i]) {
        cur[u] = i;
        int v = to[i];
        if(!del[v] && dep[v] == dep[u] + 1) {
            int o = dfs(v, min(cap[i], flow));
            flow -= o;
            res += o;
            cap[i] -= o;
            cap[i ^ 1] += o;
        }
    }
    return res;
}
int dinic() {
    int ans = 0;
    while(bfs()) ans += dfs(0, n);
    return ans;
}
void recover() {
    rep(i, 2, tot) 
        if(i & 1) cap[i] = 0;
        else cap[i] = 1;
    memset(del, 0, sizeof del);
}
void dfs(int u) {
    vis[u] = 1;
    for(int i = hd[u]; i; i = nxt[i]) 
        if(!vis[to[i]] && !cap[i]) dfs(to[i]);
}
signed main() {
#ifdef ONLINE_JUDGE
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
#endif
    cin >> n >> m;
    rep(i, 1, m) {
        int u, v; cin >> u >> v;
        c[u][v] = 1;
    }
    rep(k, 1, n) rep(i, 1, n) rep(j, 1, n)
        c[i][j] |= c[i][k] & c[k][j];
    t = n * 2 + 1;
    rep(i, 1, n) rep(j, 1, n) 
        if(c[i][j]) add(i, j + n, 1), add(j + n, i, 0);
    rep(i, 1, n) 
        add(0, i, 1), add(i, 0, 0), add(i + n, t, 1), add(t, i + n, 0);
    int l = n - dinic();
    cout << l << endl;

    vis[0] = vis[t] = 1;
    for(int i = hd[t]; i; i = nxt[i])
        if(!cap[i]) dfs(to[i]);
    rep(i, 1, n) s1.push_back(!vis[i] && vis[i + n] ? '1' : '0');
    cout << s1 << endl;

    rep(i, 1, n) {
        recover();
        del[i] = del[i + n] = 1;
        int t = n - 1;
        rep(j, 1, n) if(c[i][j] | c[j][i]) del[j] = del[j + n] = 1, --t;
        s2.push_back(t - dinic() == l - 1 ? '1' : '0');
    }
    cout << s2 << endl;
    return 0;
}
缝合题：CF590E Birthday

给定 \(n\) 个仅包含 \(\texttt{a,b}\) 的字符串，保证它们两两不同。

你需要留下尽可能多的字符串，使得这些字符串中不存在某一个串是另一个串的子串，输出方案。

\(n\le750,\sum_{i=1}^n|s_i|\le10^{7}\)。

标签：二分,匹配,int,cap,笔记,学习,dep,add,define
From： https://www.cnblogs.com/untitled0/p/bipartite-graph.html

相关文章

  • 2023烟台7天编程集训笔记3
    次小生成树：第二小的生成树。次小生成树：删掉一条边，再加上一条边，使得差值尽量小，并且要是一个树。次小生成树：如果一条边在最小生成树上，我们就叫他树边，如果不在最小生成树上就叫他非树边。次小生成树：删掉一条树边，加上一条非树边。次小生成树：倍增LCA询问环上最大的值（章鱼图）。从......
  • Docker学习路线3：安装设置
    Docker提供了一个名为DockerDesktop的桌面应用程序，简化了安装和设置过程。还有另一个选项可以使用Docker引擎进行安装。DockerDesktop网站Docker引擎DockerDesktopDockerDesktop是一款易于安装的应用程序，可使开发人员快速在其台式机上设置Docker环境。它适用于Windows和......
  • newcoder61132D <最短路 二分答案>
    题目松鼠回家思路对n个结点的松果个数排序,二分最大松果个数check(x),跑最短路,在不访问比x松果个数多的节点的情况下,从起点到终点消耗的最小体力代码Code#include<iostream>#include<algorithm>#include<vector>#include<cstring>#include<queue>using......
  • 2023烟台7天编程集训笔记2
    倍增点击查看代码//最大值不支持减法操作//倍增代码，求区间的最大值#include<bits/stdc++.h>usingnamespacestd;intn,a[1000000],f[100000][20];//f的j次方开到20就可以达到1000000intx[100010];//x[i]代表长度为i的区间，用两个长度为2^x[i]的区间能够覆盖intmain()......
  • Spring Boot 笔记
    起步依赖SpringBoot默认导入父工程依赖spring-boot-starter-parent，它里面已经申明好了众多的可能会用到的依赖。比如常用的spring-boot-starter-web，我们需要用什么，就在自己的pom.xml文件中定义就好了。<parent><groupId>org.springframework.boot</groupId><artifac......
  • 【学习笔记】Tarjan
    前言：凡事都得靠自己--bobo催隔壁K8Hen天了让他写Tarjan的学习笔记，但貌似还没有动静，所以决定自己写一个。正文本文配套题单：14.图论-tarjan（强连通分量、割点、割边）前置知识熟练使用链式前向星强连通、强连通图、强连通分量的定义（详见oi-wiki，这里不再赘述）如图......
  • 5.2 随机森林在巨量数据中的增量学习
    集成学习是工业领域中应用最广泛的机器学习算法。实际工业环境下的数据量往往十分巨大，一个训练好的集成算法的复杂程度与训练数据量高度相关，因此企业在应用机器学习时通常会提供强大的计算资源作为支持，也因此当代的大部分集成算法都是支持GPU运算的（相对的，如果你发现一个算法在任何......
  • 2023烟台7天编程集训笔记
    sort函数：把数组从小到大排序max函数：求出两个数的最大值min函数：求出两个数的最小值unique函数：使用前提是先排好序，再使用，效果是去重merge_sort归并排序reverse函数：翻转数组random_shuffle函数：把a[1]到a[n]随机打乱swap函数：交换两个数没有单调性不能二分位运算运行速度比加......
  • Django框架学习-Celery的使用
    celery用户文档：https://docs.celeryq.dev/en/v5.3.1/userguide/index.html1、Celery的提出用户需要在网站填写注册信息，发给用户一封注册激活邮件到邮箱，如果由于各种原因，这封邮件发送所需时间较长，那么客户端将会等待很久，造成不好的用户体验。——> 将耗时任务放到后台异步执行，从......
  • [刷题笔记] Luogu P4017 最大食物链计数
    ProblemDescription首先明确，最大食物链指生产者到顶级消费者（即最高营养级），而不是最长的食物链这样，我们就可以将题意转化为：在一张图中，求入度为0的点到出度为0的点路径数量这不妥妥的拓扑排序嘛（这题竟然在dp训练题单里，想了好久的dp）Solution虽说是拓扑排序，但并不完全是。我们......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99