前言：

凡事都得靠自己 --bobo

催隔壁 K8He n 天了让他写Tarjan的学习笔记，但貌似还没有动静，所以决定自己写一个。

正文

本文配套题单：14.图论-tarjan（强连通分量、割点、割边）
前置知识
1. 熟练使用链式前向星
2. 强连通、强连通图、强连通分量的定义（详见oi-wiki，这里不再赘述）
3. 如图(~~从学校课件上扒下来的图~~)，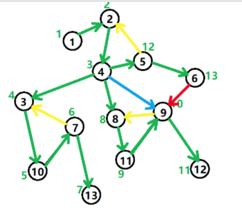
- ${\color{green}树边}$： $DFS$ 时经过的点，即 $DFS$ 搜索树上的边。
- ${\color{yellow}返祖边}$：也叫回边，与 $DFS$ 方向相反，从某个结点指向其某个祖先的边。
- ${\color{red}横叉边}$: 从某个结点指向搜索树中另一子树终端某结点的边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先时形成的。
- ${\color{blue}前向边}$: 指向子树中节点的边，父节点指向子孙结点。
  - PS：前向边无用，因为通过树边就能直接到达这个点。
- 返祖边与树边必定构成环，横叉边可能与树边构成环。
- 无向图不存在横叉边。
- 如果节点 $x$ 是某个强连通分量在搜索树中遇到的第一个节点，那么这个强连通分量的其余结点肯定在搜索树中以 $x$ 为根的子树中，节点 $x$ 被称为这个强连通分量的根。
3.时间戳、追溯值
- 时间戳 $dfn$ :用来标记某个节点在进 $DFS$ 时被访问的时间顺序（由小到大）。
- 追溯值 $low$ :用来表示从当前节点 $x$ 作为搜索树的根节点出发，能够访问到的所有节点中，时间戳 ($dfn$)最小的值。
- 当 $dfn[x]==low[x]$ 时，以 $x$ 为根的搜索子树中所有节点是一个强连通（从栈顶到 $x$ 的所有节点）分量。
- $low[x]$ 的计算方法
  - 如果 $x->y$ 是树边（没有被访问过），那么 $low[x]=min(low[x],low[y])$ 。
  - 如果 $x->y$ 是返祖边（访问过，且在栈中），那么 $low[x]=min(low[x],dfn[y])$ 。
  - 如果 $x->y$ 是横叉边（不在栈中），那么什么都不做。
```
for(i=head[x];i!=0;i=e[i].next)
{
    if(dfn[e[i].to]==0)
    {
        tarjan(e[i].to);
        low[x]=min(low[x],low[e[i].to]);
    }
    else
    {
        if(ins[e[i].to]==1)//ins[x]表示x是否在栈内
        {
            low[x]=min(low[x],dfn[e[i].to]);
        }
    }
}
```
4.时间复杂度 $O(N+M)$
- 运行Tarjan算法的过程中，每个节点都没访问了一次，且只进出了一次栈，每条边也只被访问了一次，故时间复杂度为 $O(N+M)$ 。

强连通分量（Strongly Connected Components，SCC）

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define endl '\n'
struct node
{
    int next,to;
}e[100001];
vector<int>scc[100001];
stack<int>s;
int head[100001],dfn[100001],low[100001],ins[100001],vis[100001],c[100001],cnt=0,tot=0,ans=0;
void add(int u,int v)
{
    cnt++;
    e[cnt].next=head[u];
    e[cnt].to=v;
    head[u]=cnt;
}
void tarjan(int x)
{
    int i,k=0;
    tot++;
    dfn[x]=low[x]=tot;
    ins[x]=1;
    s.push(x);
    for(i=head[x];i!=0;i=e[i].next)
    {
        if(dfn[e[i].to]==0)
        {
            tarjan(e[i].to);
            low[x]=min(low[x],low[e[i].to]);
        }
        else
        {
            if(ins[e[i].to]==1)//说明e[i].to是祖先节点or左子树节点
            {
                low[x]=min(low[x],dfn[e[i].to]);
            }
        }
    }
    if(dfn[x]==low[x])//如果这里构成了一个强连通分量
    {
        ans++;//ans是强连通分量的编号
        while(x!=k)//将这个强连通分量内的点标记一下
        {
            k=s.top();
            ins[k]=0;
            c[k]=ans;//c[k]表示k属于哪个强连通分量内
            scc[ans].push_back(k);
            s.pop();
        }
    }
}
int main()
{
    int n,m,i,j,u,v;
    cin>>n>>m;
    for(i=1;i<=m;i++)
    {
        cin>>u>>v;
        add(u,v);
    }
    for(i=1;i<=n;i++)
    {
        if(dfn[i]==0)
        {
            tarjan(i);
        }
    }
    cout<<ans<<endl;
    for(i=1;i<=n;i++)
    {
        if(vis[c[i]]==0)
        {
            vis[c[i]]=1;
            sort(scc[c[i]].begin(),scc[c[i]].end());
            for(j=0;j<scc[c[i]].size();j++)
            {
                cout<<scc[c[i]][j]<<" ";
            }
            cout<<endl;
        }
    }
    return 0;
}

luogu P2661 [NOIP2015 提高组] 信息传递

易知本题答案为最小的强连通分量大小（非1）

scc=0;
while(x!=k)
{
    k=s.top();
    ins[k]=0;
    scc++;
    s.pop();
}
if(scc!=1)
{
    maxin=min(maxin,scc);
}

$maxin$ 即为结果

luogu P2863 [USACO06JAN] The Cow Prom S

按照题意打就行

缩点

缩点：把强连通分量看作一个大点，并保留不在此强连通分量内的边，重新建图（易知此时的图是一个 DAG ,可以进行拓扑排序)。

if(dfn[x]==low[x])
{
    ans++;
    while(x!=k)
    {
        k=s.top();
        ins[k]=0;
        c[k]=ans;
        b[ans]+=a[k];//a[]为原点权，b[]为缩点后的点权
        s.pop();
    }
}

cnt=0;
memset(e,0,sizeof(e));
memset(head,0,sizeof(head));
for(i=1;i<=m;i++)
{
    if(c[u[i]]!=c[v[i]])//Pursuing_OIer 教给我的神奇的建边方法（其实很好理解）
    {
        add(c[u[i]],c[v[i]]);
    }
}

例题
- luogu P2002 消息扩散观察题意，易知结果为缩点后入度为0的点个数
- luogu P2812 校园网络【[USACO]Network of Schools加强版】第一问显然同luogu P2002，第二问显然是要求 $max(缩点后入度为0的点的个数，缩点后出度为0的点的个数)$ , 只有一个 $SCC$ 时记得特判。
  
  ~~双倍经验~~ P2746 [USACO5.3] 校园网Network of Schools
- luogu P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G 观察题意，易知缩点后若有强连通分量的个数 $>1$ ，则无解；当只有 $1$ 个强连通分量时，这个强连通分量的大小即为所求。
- luogu P2515 [HAOI2010] 软件安装读完题，发现和luogu P2014 [CTSC1997] 选课很像，只不过选课是一棵树，本题是一个图。可能本题建图有点麻烦，剩下的话，缩点后当$树形dp做就行了。
```
for(i=1;i<=n;i++)
{
    cin>>u[i];
    v[i]=i;
    if(u[i]!=0)
    {
        add(u[i],v[i]);
    }
}

······

cnt=0;
memset(e,0,sizeof(e));
memset(head,0,sizeof(head));
for(i=1;i<=n;i++)
{
    if(c[u[i]]!=c[v[i]])
    {
        add(c[u[i]],c[v[i]]);
        din[c[v[i]]]++;
    }
}
for(i=1;i<=ans;i++)
{
    if(din[i]==0)
    {
        add(0,i);
    }
}
```
- luogu P3387 【模板】缩点缩点后跑最长路（SPFA or 拓扑）
```
int top_sort()
{
    queue<int>q;
    int i,k,num=0;
    for(i=1;i<=ans;i++)
    {
        if(din[i]==0)
        {
            q.push(i);
            dis[i]=b[i];//b[]为缩点后的点权
        }
    }
    while(q.empty()==0)
    {
        k=q.front();
        q.pop();
        for(i=head[k];i!=0;i=e[i].next)
        {
            dis[e[i].to]=max(dis[e[i].to],dis[k]+b[e[i].to]);
            din[e[i].to]--;
            if(din[e[i].to]==0)
            {
                q.push(e[i].to);
            }
        }
    }
    for(i=1;i<=ans;i++)
    {
        num=max(num,dis[i]);
    }
    return num;
}
```
  加强版->P3627 [APIO2009] 抢掠计划增加了起点和终点限制（缩点时要进行存储），但总体改变不大，拓扑不太好打，所以就换SPFA了，代码。