状压 DP
状压 DP,是通过将状态压缩为整数来达到优化转移目的的一类 DP。
一般的,若集合大小不超过 \(n\),集合中每个元素都是小于 \(k\) 的自然数,我们可以把这个集合看作一个 \(n\) 位 \(k\) 进制数,以一个 \([0,k^n-1]\) 之间的十进制整数的形式作为 DP 状态的一维。
而状压 DP,最常见的就是压成二进制数,例如 \(0\) 表示未被访问,\(1\) 表示被访问两个值。我们可以想象 DP 的轮廓以访问过的节点数目为阶段,从 \((0,0,\dots,0)\) 扩展到 \((1,1,\dots,1)\)。为了记录当前状态在每个维度上是 \(0\) 还是 \(1\),我们使用一个 \(n\) 位二进制数,即 \([0,2^n-1]\) 之前的十进制整数存储节点的访问情况。
由此可以看出,DP 的状态由访问过的节点数目和访问哪些节点组成,状态大小分别是 \(n\) 和 \(2^n\)。所以你会发现状压 DP 的题往往 \(n\) 都是比较小的,因为我们要通过压缩二进制来描述状态。
前置
常见的状压 DP 涉及到很多二进制的操作,学会这些操作,我们才能高效地进行状压 DP。
具体你可以看这篇博客,并且这里再补充一个枚举子集的位运算:
for(int i=(s-1)&s;i;i=(i-1)&s)
基础
在 \(N\times N\) 的棋盘里面放 \(K\) 个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共 \(8\) 个格子。
\(1\leq N \leq 9,0 \leq K \leq N\times N\)。
按照上文的思想,我们设 \(f(i,j,l)\) 表示前 \(i\) 行,第 \(i\) 行的状态为 \(j\),且棋盘上已经放置 \(l\) 个国王的合法方案数。
对于编号为 \(j\) 的状态,我们用 \(s_j\) 表示国王的放置情况,\(s_j\) 的某一位若为 \(0\),代表这个位置不放国王;若放,则为 \(1\)。并且,我们用 \(g_j\) 来存储当状态为 \(s_j\) 时,这个状态放置了多少个国王。引用 OI-Wiki 上的图片:

如下图,\(s_j = 101001_{(2)},g_j =3\)。
设上一行的状态为 \(k\),由于当前行的放置方案跟上一行有关,但跟上上行无关,所以我们转移的时候只需要关心上一行的状态即可,那么就有:
\[f(i,j,l) =\sum_{\text{一些限制条件}} f(i-1,k,l-g_j) \]这些限制条件根据题目得来,在这个题中,因为国王能打到下方,左下方和右下方,所以我们要判断 \(s_k\) 是否是一个合法的 \(s_j\) 的上一行,用代码写出来,就是:
if(!(s[j] & s[k]) && !(s[j] & (s[k]<<1)) && !(s[j] & (s[k]>>1))) return true;
这就是我们为什么要用位运算的原因:方便简洁。
还有一个对于大多数状压 DP 的优化:减少状态个数。由于题目的限制,我们发现,在同一行内,不能有两个相邻的国王,所以这就提示我们可以预处理出 \(s_j\),排除掉不合法的状态,再在合法的状态里进行转移,这样往往能大幅度的优化复杂度。
il void init()
{
for(re int i=0;i<(1<<n);i++)
{
if((i & (i>>1)) || (i & (i<<1))) continue;//排除不合法状态
s[++cnt] = i;
}
for(re int i=1;i<=cnt;i++) g[i] = __builtin_popcount(s[i]);
}
signed main()
{
n = read() , m = read();
init();
for(re int i=1;i<=cnt;i++) f[1][i][g[i]] = 1;//第一行先预处理一下
for(re int i=2;i<=n;i++)
for(re int j=1;j<=cnt;j++)
{
numj = g[j];
for(re int k=1;k<=cnt;k++)
{
if((s[j] & s[k]) || (s[j] & (s[k]<<1)) || (s[j] & (s[k]>>1))) continue;
numk = g[k];
for(re int l=0;l<=m;l++)
f[i][j][l+numj] += f[i-1][k][l];//刷表法更新更加简洁
}
}
for(re int i=1;i<=cnt;i++) ans += f[n][i][m];
cout << ans;
return 0;
}
与之类似的习题还有 P2704 [NOI2001] 炮兵阵地、P1879 [USACO06NOV] Corn Field G,可以尝试着做一做。
枚举子集
这里贴一篇 yxc 的博客,就不细说了。
状态压缩DP,下文中 \(i\) 是一个 \(n\) 位二进制数,表示每个点是否存在。
状态 \(f(i,j)\) 表示:
-
集合: 所有包含 \(i\) 中所有点,且树的高度等于 \(j\) 的生成树
-
属性: 最小花费
状态计算:枚举 \(i\) 的所有非全集子集 \(S\) 作为前 \(j-1\) 层的点,剩余点作为第 \(j\) 层的点。
核心:求出第 \(j\) 层的所有点到 \(S\) 的最短边,将这些边权和乘以 \(j\),直接加到 \(f(S,j-1)\) 上,即可求出 \(f(i,j)\)。
证明:
将这样求出的结果记为 \(f'(i,j)\)
-
\(f(i,j)\) 中花费最小的生成树一定可以被枚举到,因此 \(f(i,j)\ge f'(i,j)\);
-
如果第 \(j\) 层中用到的某条边 \((a, b)\) 应该在比 \(j\) 小的层,假设 \(a\) 是 \(S\) 中的点,\(b\) 是第 \(j\) 层的点,则在枚举 \(S+\{b\}\) 时会得到更小的花费,即这种方式枚举到的所有花费均大于等于某个合法生成树的花费,因此 \(f(i,j)\leq f'(i,j)\)
所以有 \(f(i,j)=f'(i,j)\)。
这一段想要表明的是:在枚举的时候,我们一定不会漏下一棵最优的生成树,假如这条边在这里不是最优的,那么一定存在一个生成树能让这条边在最优的位置上。
时间复杂度
包含 \(k\) 个元素的集合有 \(\displaystyle \binom{n}{k}\) 个,且每个集合有 \(2^{k}\) 个子集,因此总共有 \(\displaystyle \binom{n}{k} 2^{k}\) 个子集。 \(k\) 可以取 $0 \sim n $,则总共有 \(\displaystyle \sum_{k=0}^{n} \binom{n}{k} 2^{k}=(1+2)^{n}=3^{n}\) ,这一步由二项式定理可得。
对于每个子集需要 \(n^{2}\) 次计算来算出剩余点到子集中的最短边。
因此总时间复杂度是 \(\mathcal O(n^{2} 3^{n})\)。
数位 DP
在给出具体例子前,我们先不加解释地给出数位 DP 的一些特点或技巧
特点或技巧
特点
数位 DP 往往是求解某个区间 \([L,R]\) 内,满足某种性质的数的个数。
技巧
-
1.我们往往运用类似前缀和的思想,转化为 \([0,R] - [0,L-1]\) 求解。
-
2.从高位到低位填数,往往要分类讨论:
我们把整数 \(R\) 的每一位分离出来,存入数组 \(a\),则 \(R = a_na_{n-1}\dots a_1\),从高位到低位填数,划分为两类;\(0\sim a_{i-1}\) 和 \(a_i\)。
-
如果第 \(i\) 位填 \(0\sim a_{i-1}\),则后面每一位可以填 \(0\sim 9\);
-
如果第 \(i\) 位填 \(a_i\),那么再讨论下一位。这样,保证填的数不超过 \(R\)。
这样的思想往往可以通过一个树形图表示出来,数形结合,更容易理解。
-
例题
科协里最近很流行数字游戏。某人命名了一种不降数,这种数字必须满足从左到右各位数字成小于等于的关系,如 \(123,446\)。现在大家决定玩一个游戏,指定一个整数闭区间 \([a,b]\),问这个区间内有多少个不降数。
\(0 \leq a \leq b \leq 2^{31}-1\)
显然,暴力枚举是会超时的,我们考虑换一个角度来考虑。
我们采用上文所说的树形图来叙述。
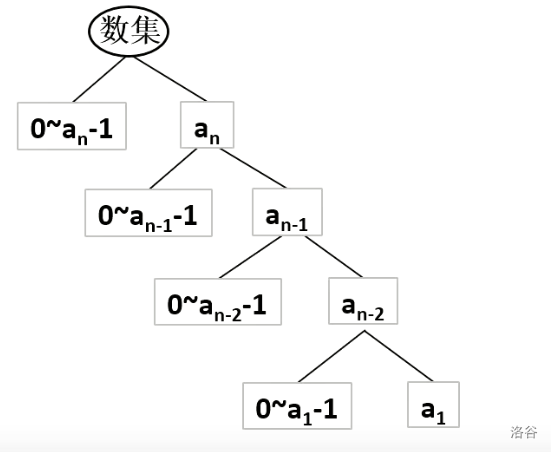
我们发现,当第 \(n\) 位是 \(0\sim a_n-1\) 时,后面 \(n-1\) 位的范围是从 \(00\dots 000\) 到 \(99\dots 999(n-1\text{个})\) 随便选的。同理,当 \(a_n=1\),而第 \(n-1\) 位取 \(0\sim a_{n-1}-1\) 时,后 \(n-2\) 位是随便选的,以此类推。
我们可以发现,不降数的个数应该与位数以及最高位的数字有关,对此,我们可以预处理出来,并把它运用到从 \(000..\) 选到 \(999..\) 这个过程中,因为它们的选取是没有限制的。
设 \(f(i,j)\) 表示一共有 \(i\) 位,且最高位数字为 \(j\) 的不降数的个数。
考虑从小到大的转移,因为最高位已经固定为 \(j\),所以假设第 \(i-1\) 位是 \(k\),根据不降数的定义 \(k\ge j\),所以有
\[f(i,j) = \sum_{k=j}^9 f(i-1,k) \]const int N = 12;//最高位数有多少
il void init()
{
for(re int i=0;i<=9;i++) f[1][i] = 1;//一位先预处理出来
for(re int i=2;i<N;i++)
for(re int j=0;j<=9;j++)
for(re int k=j;k<=9;k++)
f[i][j] += f[i-1][k];
}
之后我们就可以按照树形图的思想,一步一步的往下找就行了。
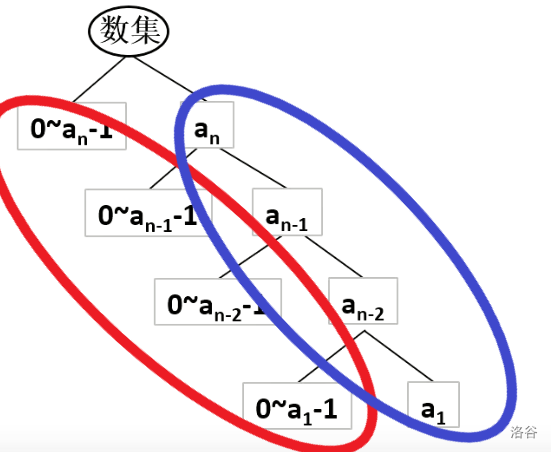
我们发现答案集合就在这两个圆圈里面,且右边的这个答案集合其实就是 \(R\) 这一个数。并且,比方说当我们已经求出了 \(0\sim a_k-1\),将要从 \(a_k\) 开始去求 \(a_{k-1}\) 这一层了,然后这时候你发现 \(a_n \sim a_k\) 构成的这个数已经不满足题意了,那么后面的答案就都是非法的了,因为它们的前缀都是一样的,这时候就可以 break 掉了,当我们到达最底层的时候,不要忘记这说明 \(R\) 本身也是合法的,不要忘记统计它的贡献,也就是 ans++。
il int Get_ans(int n)
{
if(!n) return 1;//特判n==0
cnt = res = 0;
while(n) a[++cnt] = n % 10 , n /= 10; //拆分
int last = 0;//last表示上一个数是多少,也就是 a_i
for(re int i=cnt;i>=1;i--)//高位到低位
{
int now = a[i];//now表示这一位的数
for(re int j=last;j<now;j++)//不降
res += f[i][j];//后面的随便取
if(now < last) break;//不合法
last = now;
if(i == 1) res++;//R本身合法
}
return res;
}
signed main()
{
l = read() , r = read();
cout << Get_ans(r) - Get_ans(l-1);//转化
}
这就是这个题的大致思路。
洛谷题单提供了大量练习题,可以去写一写。
写了一些之后,你就会发现,数位 DP 的模式基本都是类似的,都可以写成下面的这个伪代码:
il void init()
{
预处理我们想要的 f 数组
}
il int Get_ans(int n)
{
if(!n) ....;//特判n==0
cnt = res = 0;
while(n) a[++cnt] = n % 10 , n /= 10; //拆分
int last = 0;//last表示上一个数是多少,也就是 a_i
for(re int i=cnt;i>=1;i--)//高位到低位
{
int now = a[i];//now表示这一位的数
for(j 在这一位能取的值)//不降
res += f;//后面的随便取
if(...) break;//不符合题目给的条件了
last = now;
if(i == 1) res++;//R本身合法
}
return res;
}
signed main()
{
init();
l = read() , r = read();
cout << Get_ans(r) - Get_ans(l-1);
}
数位 DP 大致就是这样的。
标签:状态,int,leq,枚举,sim,动态,规划,DP From: https://www.cnblogs.com/bloodstalk/p/17538320.html