差分
一维差分
What
差分可理解为前缀和的逆运算 前缀和
背景
现有数组 \(A\),需构造数组 \(B\).
使得 \(a_i = b_1 + b_2 + \cdots + b_i\).
\(A\) 数组为原数组,\(B\) 数组即为 \(A\) 的差分数组。
\(b_1\) 的值
\[\begin{aligned} &\because a_1 = b_1 \\ &\therefore b_1 = a_1 \end{aligned} \]\(b_2\) 的值
\[\left\{\begin{aligned} & a_1 = b_1 \\ & a_2 = b_1 + b_2 \end{aligned}\right. \]\[\begin{aligned} b_2 &= (b_1 + b_2)-b_1\\ &=a_2 - a_1 \end{aligned} \]\(b_3\) 的值
\[\left\{\begin{aligned} & a_2 = b_1 + b_2 \\ & a_3 = b_1+b_2+b_3 \end{aligned}\right. \]\[\begin{aligned} b_3 &= (b_1 + b_2 + b_3)-(b_1 + b_2)\\ &=a_3 - a_2 \end{aligned} \]\(b_i\) 的值
\[\left\{\begin{aligned} & a_1 = b_1 \\ & a_2 = b_1 + b_2 \\ & \dots \\ & a_{i - 1} = b_1+b_2+\cdots+b_{i-1}\\ & a_i = b_1+b_2+\cdots+b_{i - 1}+b_i \end{aligned}\right. \]\[\begin{aligned} b_i &= (b_1+b_2+\cdots+b_{i - 1}+b_i)-(b_1+b_2+\cdots+b_{i-1})\\ &=a_i - a_{i-1} \end{aligned} \] 简而言之,
\(b_i = a_i-a_{i-1}\)
怎么用
作用1
现有数组 \(A\),需构造数组 \(B\).
使得 \(a_i = b_1 + b_2 + \cdots + b_i\).
\(A\) 数组为原数组,\(B\) 数组即为 \(A\) 的差分数组。
所以,对 \(B\) 数组求一遍前缀和即能得到 \(A\) 数组。
由 \(B\) 数组可通过 \(O(N)\) 得到 \(A\) 数组。(通过前缀和)
作用2
使区间 \(\left[l, r\right]\) 的 \(A\) 数组元素都加上 \(c\).
即
只需要对 \(B\) 进行操作
只需 \(b_l + c\) 且 \(b_{r+ 1} - c\),然后来一遍前缀和,就能得到使区间 \(\left[l, r\right]\) 的元素都加上 \(c\) 的 \(A\) 数组了。
以下是解释(证明)
通过简单观察(思考),得到以下结论:
- \(b_i + c\) 后再通过前缀和得到 \(A\) 时,\(A\) 中 区间 \(\left[ i, n\right]\) 元素都会 加上 \(c\).
- \(b_i - c\) 后再通过前缀和得到 \(A\) 时,\(A\) 中 区间 \(\left[ i, n\right]\) 元素都会 减去 \(c\).
所以,只需 \(b_l + c\) 且 \(b_{r+1} - c\),然后来一遍前缀和,就能得到使区间 \(\left[l, r\right]\) 的元素都加上 \(c\) 的 原数组 \(A\) 数组了。
复杂度由 \(O(N)\) 降到了 \(O(1)\).
所以 \(A, b\) 数组可理解为初始值均为 \(0\).
当 \(A\) 被赋值时,可理解为区间 \([i,i]\) 中的元素加上 \(a_i\).
可用这种方式思考如何构造。
模板
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
例题 link
AcWing 797. 差分 题目入口
题目大意
输入一个长度为 \(n\) 的整数序列。
接下来输入 \(m\) 个操作,每个操作包含三个整数 \(l,r,c\),表示将序列中 \([l,r]\) 之间的每个数加上 \(c\)。
请你输出进行完所有操作后的序列。
CODE
点击查看代码1
/*
a, b 数组可理解为均为0.
当a被赋值时,可理解为[i,i]中的元素加上b[i]
*/
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], b[N];
void insert(int l, int r, int c) // 模块化
{
b[l] += c;
b[r + 1] -= c;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )
insert(i, i, a[i]);
while (m -- )
{
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
for (int i = 1; i <= n; i ++ ) // 前缀和处理
b[i] += b[i - 1];
for (int i = 1; i <= n; i ++ )
printf("%d ", b[i]);
return 0;
}
点击查看代码1
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int m, n;
int a[N], b[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
cin >> a[i];
b[i] = a[i] - a[i - 1];
}
while (m -- )
{
int l, r, c;
cin >> l >> r >> c;
b[l] += c, b[r + 1] -= c;
}
for (int i = 1; i <= n; i ++ )
{
a[i] = a[i - 1] + b[i];
cout << a[i] << ' ';
}
return 0;
}
二维差分
同样,二维差分与一维差分是一样的道理。
What
有原矩阵 \(a_{i,j}\),差分矩阵 \(b{i,j}\).
同样的,只需要原矩阵 \(A\) 是差分矩阵 \(B\) 的前缀和矩阵即可。
即
\[a_{i,j}=a_{i-1,j}+a_{i,j-1}-a_{i-1,j-1}+b_{i,j} \]所以,
\[b_{i,j} = a_{i,j}-a_{i-1,j}-a_{i,j-1}+a_{i-1,j-1} \]作用
给其中的一个子矩阵加上 \(c\).
令这个子矩阵的左上端点为 \((x_1, y_1)\),右下端点为 \((x_2,y_2)\).
只需要 \(b_{x_1,y_1} + c\), \(b_{x_2+1,y_1} - c\), \(b_{x_1,y_2+1} - c\), $b_{x_2+1,y_2+1} + c, $
解释/证明
结论:
- \(b_{i,j} + c\) 后再通过前缀和得到 \(A\) 时,\(A\) 中 区左上端点为 \((i, j)\),右下端点为 \((m,n)\) (矩阵右下角)的矩阵 中所有元素都会加上\(c\).
- \(b_{i,j} - c\) 后再通过前缀和得到 \(A\) 时,\(A\) 中 区左上端点为 \((i, j)\),右下端点为 \((m,n)\) (矩阵右下角)的矩阵 中所有元素都会减去\(c\).
所以,如图
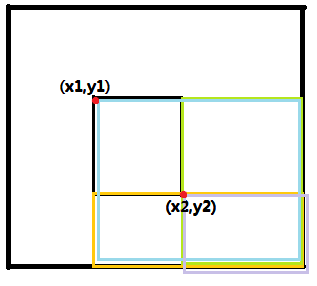
便能得到
只需要 \(b_{x_1,y_1} + c\), \(b_{x_2+1,y_1} - c\), \(b_{x_1,y_2+1} - c\), $b_{x_2+1,y_2+1} + c, $
构造二维差分也可以理解为在一个仅由一个元素组成的矩阵(左上端点为 \((i, j)\),右下端点也为 \((i,j)\))中所有元素加上 \(a_{i,j}\)
模板
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
模板题
AcWing 798. 差分矩阵 题目入口
题目大意
输入一个 \(n\) 行 \(m\) 列的整数矩阵,再输入 \(q\) 个操作,每个操作包含五个整数 \(x1,y1,x2,y2,c\),其中 \((x1,y1)\) 和 \((x2,y2)\) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 \(c\)。
请你将进行完所有操作后的矩阵输出。
CODE
点击查看代码1
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
insert(i, j, i, j, a[i][j]);
while (q -- )
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; // 前缀和
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
printf("%d ", b[i][j]);
puts("");
}
return 0;
}