如果一个 DP 的转移方程可以写成 \(f_i=\underset{j<i}{\min\!/\!\max}\>\{f_j+a_i\times b_j+c_i+d_j\}+C\) 的形式,那么可以运用斜率优化。
不妨设转移是 \(\min\),设 \(g_{i,j}=f_j+a_i\times b_j+c_i+d_j\),即 \(f_i=\min\limits_{j<i}g_{i,j}\),式子可以化为 \(f_j+d_j=-a_i\times b_j+g_{i,j}-c_i\),设 \(y_j=f_j+d_j\),\(k=-a_i\),\(x_j=b_j\),\(t_j=g_{i,j}-c_i\),原式化为 \(y_j=kx_j+t_j\quad(*)\),这是一个一次函数的形式。
假设 \(f_i\) 是由 \(p\) 转移来的,即 \(f_i=g_{i,p}=\min_{j<i}g_{i,j}\),因为 \(t_j=g_{i,j}-c_i\),所以 \(t_p=\min_{j<i}t_j\)。 注意到 \((*)\) 式中 \(k\) 是一个定值,这说明,如果过每个点 \((x_j,y_j)\) 画斜率为 \(k\) 的直线 \(l_j\),则 \(l_p\) 在 \(y\) 轴的截距是最小的,直观地说就是“在最下面”的。
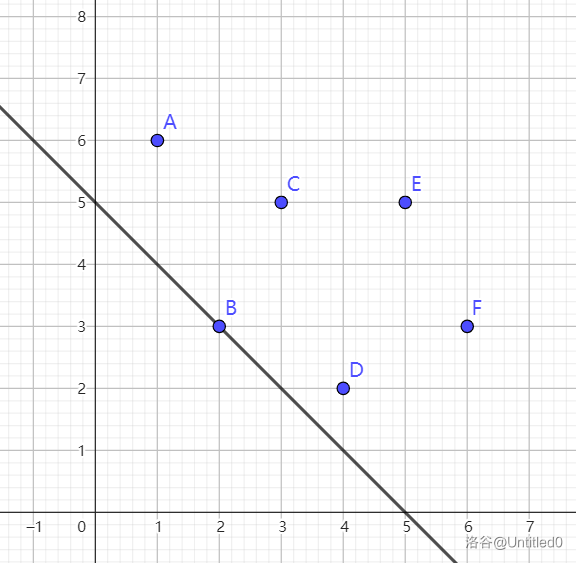
(如图,假设有这些点,我们要画一条斜率为 \(-1\) 的直线(\(k=-1\)),则图中那条是最优的,其 \(y\) 轴截距是 \(5\),最小)
现在考虑如何快速找到这条最优直线:维护这些点的下凸壳,则与这个凸壳相切的直线是最优的。(这里“相切”的定义是,有且仅有一个交点 或 有无数个交点)
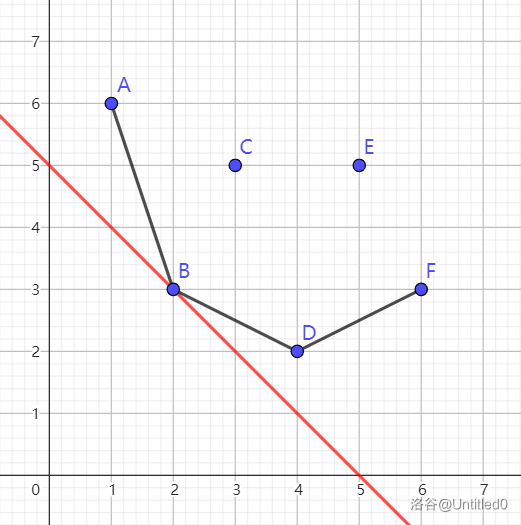
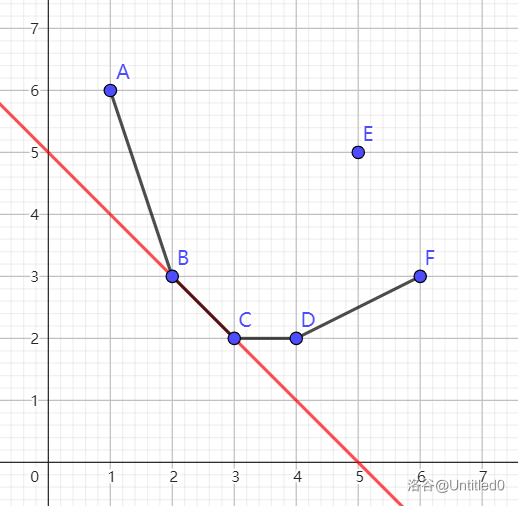
(如图,两种相切)
维护这个东西需要动态凸包,但是一般情况下并不需要:
- 如果 \(x\) 单调,\(k\) 也单调,则决策点 \(p\) 只会单向移动,单调队列维护即可。
- 如果 \(x\) 单调,用单调栈维护凸壳,然后二分即可。
- 否则需要动态凸包 / 李超线段树。(我不会)