一、案例介绍
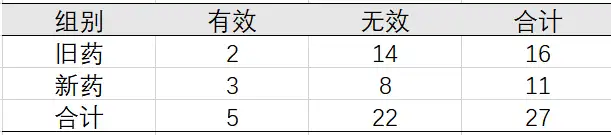
某医生用新旧两种药物治疗某病患者27人,治疗结果见下表,现在想知道两种两种药物的治疗效果有无差别?
二、问题分析
本案例的分析目的是探究两种治疗效果有无差异,总样本量为27<40,所以考虑使用四格表Fisher确切检验法进行分析,但是需要满足2个条件:
条件1:分组变量和观察变量均为二分类变量;本案例数据组别和治疗效果都是二分类变量,满足该条件。
条件2:观测值之间相互独立;本案例中27名患者之间都是独立的,治疗效果不存在互相干扰情况,满足该条件。
所以,可以使用四格表Fisher确切检验法进行分析。
三、软件操作及结果解读
(一)理论说明
四格表Fisher确切检验法的基本思想是:在周边合计数保持不变的条件下,计算表内4个实际频数变动时的各种组合之概率Pi;再按检验假设用单侧或双侧的累计概率P,依据所取的检验水准α做出推断。
Fisher确切检验法是由R.A.Fisher于1934年提出的,是基于超几何分布理论直接计算拒绝零假设的概率的,所以不会有卡方值。该方法依据超几何分布,利用排列的数学原理进行计算,计算量比较大,不适合手算,故使用软件计算直接得到p值进行判断。
(二)软件操作
在SPSSAU实验/医学研究模块,选择【Fisher卡方】。按照提示,在表格中填写案例数据,注意A1单元格一定要空着,且不需要填写汇总数据,操作如下图:

(三)结果解读
1、检验统计量表格
SPSSAU输出检验统计量结果如下:
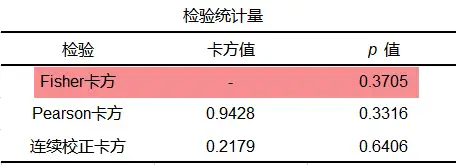
从上表可知,Fisher确切检验对应的p值为0.3705,>0.05,所以不能拒绝原假设,即尚不能认为两种药物的治疗效果不同。
同时可以看到,除了Fisher卡方外,SPSSAU同时输出Pearson卡方值和连续校正卡方值以及分别对应的p值,从p值结果来看,3个值均呈现出一致性结论,即尚不能认为两种药物的治疗效果不同。
那么3种卡方值具体应该如何选择呢?需要看期望频数表格进行判断。
2、期望频数表格
SPSSAU输出案例期望频数如下:
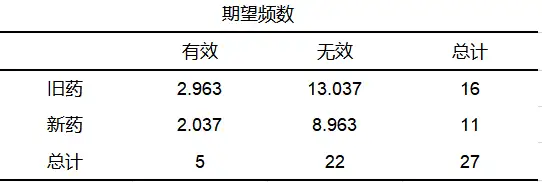
通常情况下:
如果总样本量大于40且期望频数值全部均大于5时,一般使用Pearson卡方值;
如果总样本量大于40,但出现期望频数小于5的单元格时,可优先使用连续校正卡方,也或者使用fisher卡方值;
如果总样本量小于40,也或者出现期望频数小于1的单元格时,此时建议使用fisher卡方检验。
由此我们也明白了为什么在第二部分问题分析时提出,本案例总样本量为27小于40,所以使用Fisher确切检验法进行分析。
四、结论
本案例采用2*2Fisher确切检验法对新药和旧药的治疗效果进行比较分析,由于总样本量27<40,且满足Fisher确切检验法需要满足的条件,所以采用该方法进行分析。分析结果显示,Fisher确切检验法对应的p值为0,3705>0.05,所以不能拒绝原假设,两种药物的治疗效果差异无统计学意义,即尚不能认为新药和旧药两种药物的治疗效果不同。
五、知识小贴士
(1)三类卡方检验值应该看哪种?
通常情况下:如果总样本量>40且期望频数值全部均大于5时,一般使用pearshon卡方值;如果总样本量大于40,但出现期望频数小于5的单元格时,可优先使用连续校正卡方,也或者使用fisher卡方值;
如果总样本量小于40,也或者出现期望频数小于1的单元格时,此时建议使用fisher卡方检验。具体以文献为准即可,可能不同文献的标准不完全一致。
(2)期望频数如何计算?
我们称每个观测变量出现的次数为频数,期望频数是频数的期望值。对于r*c行列表,第r行第c列格子中观察频数O_{r c}对应的期望频数为E_{r c}=\frac{n_{r}n_{c}}{n},其中n_{r}为第r行的合计数,n_{c}为第c列的合计数,n为总样本量。
如本案例中,第1行1列旧药有效数为2,则其期望频数为5*16/27=2.963;其余计算类似。
参考文献:
[1]颜红,徐勇勇.医学统计学.第3版[M].人民卫生出版社,2015
标签:频数,期望,40,检验,四格,卡方值,Fisher,样本量,fisher From: https://www.cnblogs.com/spssau/p/17516061.html