几何题2

$ \triangle ABC $ 的内心为 \(I\)，内切圆分别切边 \(BC\)、\(CA\)、\(AB\) 于 \(D\)、\(E\)、\(F\)．直线 \(BI\)、\(CI\)、\(DI\) 分别交 \(EF\) 于 \(M\)、\(N\)、\(K\)．直线 \(BN\)、\(CM\) 交于点 \(P\)，直线 \(AK\)、\(BC\) 交于点 \(G\)．过 \(I\) 垂直于 \(PG\) 的直线，与过 \(P\) 垂直于 \(PB\) 的直线交于 \(Q\)．证明：直线 \(BI\) 平分线段 \(PQ\)．

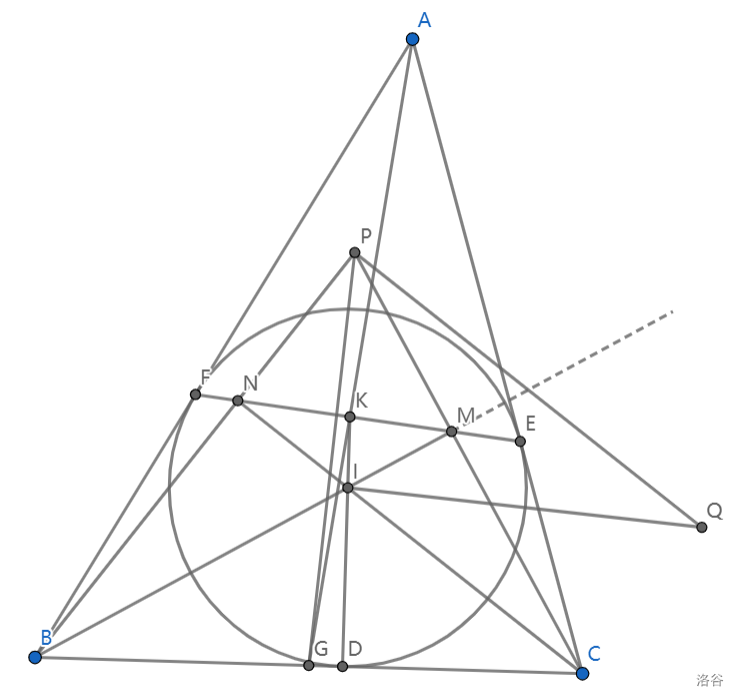
如图，设 \(BP\) 中点为 \(L\)，\(BI\) 交 \(PQ\) 于 \(J\)，连结 \(PK\)、\(IE\)、\(IF\)、\(GL\)．以下通过导出一些结论逐渐证明本题．

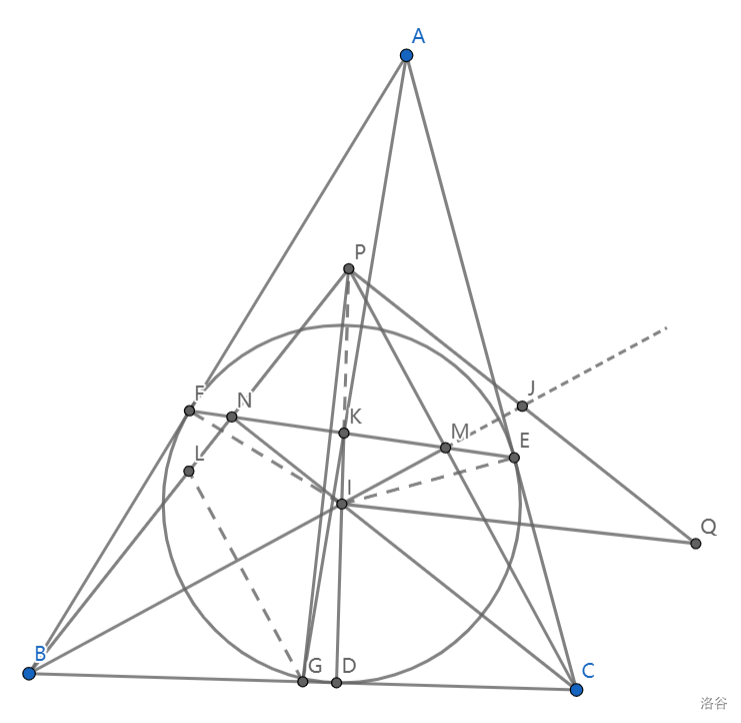
结论 \(\text{1}\)：\(N\)、\(M\)、\(C\)、\(B\) 四点共圆，且 \(BC\) 是直径．

证明：易知 \(\angle BFM = 90^\circ + \frac{\angle A}{2}\)，\(\angle FBM = \frac{\angle B}{2}\)，于是 \(\angle FMB = \frac{\angle C}{2} = \angle ACI\)，故 \(M\)、\(E\)、\(C\)、\(I\) 四点共圆，有 \(\angle BMC = \angle IEC = 90^\circ\)．同理，\(\angle BNC = 90^\circ\)，结论得证．

由此结论还可以导出 \(I\) 是 \(\triangle PBC\) 的垂心，又由于 \(KD \perp BC\)，于是 \(P\)、\(K\)、\(I\)、\(D\) 共线．

结论 \(\text{2}\)：\(G\) 是 \(BC\) 的中点．

证明：由分角定理，\(\frac{EK}{FK} = \frac{AE \cdot \sin \angle EAK}{AF \cdot \sin \angle FAK} = \frac{IE \cdot \sin \angle EIK}{IF \cdot \sin \angle FIK}\)，而 \(AE = AF\)，\(IE = IF\)，故 \(\frac{\sin \angle EAK}{\sin \angle FAK} = \frac{\sin \angle EIK}{\sin \angle FIK}\)，而 \(\frac{\sin \angle EIK}{\sin \angle FIK} = \frac{\sin \angle C}{\sin \angle B} = \frac{AB}{AC}\)，那么 \(\frac{\sin \angle EAK}{\sin \angle FAK} = \frac{AB}{AC}\)．于是 \(\frac{BG}{CG} = \frac{AB \cdot \sin \angle BAG}{ AC \cdot \sin \angle CAG} = 1\)，结论得证．

于是 \(GL\) 是中位线，有 \(GL \parallel CP\)，那么 \(\angle BGL = \angle BCP = \frac{\angle C}{2} + \angle ICM = \frac{\angle C}{2} + \angle IEF = \frac{\angle A + \angle C}{2} = 90^\circ - \frac{\angle B}{2} = \angle PIJ\)．

由于 \(PQ \perp BP\)，\(IQ \perp PG\)，\(PI \perp BG\)，故 \(\triangle BPG \sim \triangle PQI\)．而 \(\angle BGL = \angle PIJ\)，那么 \(L\)、\(J\) 是对应点，故 \(J\) 是 \(PQ\) 的中点，即 \(BI\) 平分 \(PQ\)．证毕．