目录
Prüfer 序列
Prüfer 序列是将一颗 \(n\) 个有标号的点用一个长度为 \(n-2\) 的序列的表示的方法。
对于一颗有标号的树,会存在唯一一个 Prüfer 序列与之对应。一个 Prüfer 序列也只会对应一颗树。
将一颗树转化为 Prüfer 序列
首先对于所有的叶子节点(此时为 \(1,2,4,6\)),选择其编号最小的节点删掉。然后将其父亲节点加入 Prüfer 序列中。
在重复经过 \(n-2\) 次操作后,剩余了 \(2\) 个点,构造结束。
过程
对于一颗有标号的树:
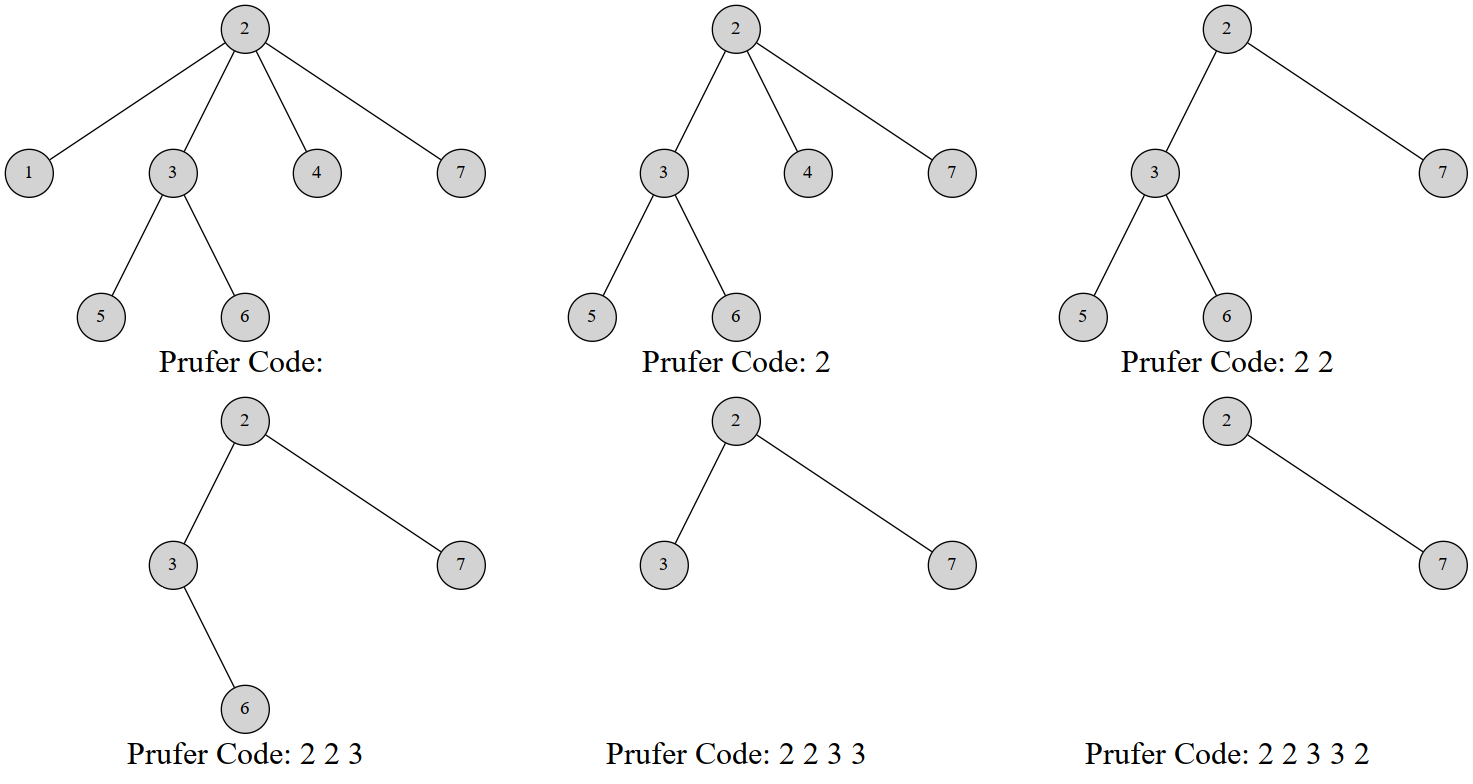
显而易见地是,1. 可以用一个大根堆来维护所有的叶子节点。
-
每次取出堆中最大的元素删除。
-
在每次删除节点后,判断它的父亲节点是否成为叶子节点,如果是,加入堆中。
这样的做法的时间复杂度是 \(\text O(n\log_2n)\) 的。
(存在线性做法,先gugu)。
性质
可以发现,在 Prüfer 序列中,每个点 \(u\) 的出现次数是其点的度数 \(d_u-1\) 。
-
对于叶子节点,一定不会存在 Prufer序列中。
-
对于非叶子节点 \(u\),在节点 \(u\) 被删掉前,会有与之相连的 \(d_u-1\) 的节点会被删掉(其原因是在构造 Prufer序列的过程中树是联通的,且树大小始终不小于 \(2\)),在这个过程中,节点 \(u\) 就会被加入 Prufer序列 \(d_u-1\) 次。
由此也可以知道 \(\sum_{i=1}^{n}(d_u-1)=n-2\)。
Prüfer 序列将转化为一颗树
过程
考虑将上述转化的过程,重复一遍。
-
对于 Prüfer 序列的第一个数 \(u\) ,和它相连的节点 \(v\) 一定是叶子节点中编号最小的。将 \(u\) 与 \(v\) 连边。
-
那么维护一个叶子节点集合 \(S\),将这个编号最小的节点 \(v\) 删掉。
-
此时将 Prüfer 序列的第一个数也删掉,由于叶子节点在 Prüfer 序列的出现次数为 \(d-1=0\),那么如果这个数在 Prüfer 序列中的出现次数为 \(0\) 的话,节点 \(u\) 变为叶子节点。
-
重复该过程。
这个过程也可以使用堆维护,当然也存在线性做法(gugu)。
性质
- 无向完全图的不同生成树数(Cayley公式)
对于一个 \(n\) 个点的无向完全图,任意一个长度为 \(n-2\) 的 Prüfer 序列都可以构造出一个不同的具有 \(n\) 个点的树。
所以讲,会有 \(n^{n-2}\) 个不同的 Prüfer 序列构成 \(n\) 个点的树,那么无向完全图的不同生成树数也就是 \(n^{n-2}\) 个。
- \(n\) 个点无根树计数,且已知每个点的点度。
由于每个点在 Prüfer 序列中的出现次数为 \(d_i-1\),所以可以利用组合知识求出。
\[\binom{n-2}{b_1-1}\cdot\binom{(n-2)-(b_1-1)}{b_2-1}\cdots\binom{b_n-1}{b_n-1} \]展开可以得到
\[\frac{(n-2)!}{\prod_{i=1}^{n}(b_i-1)} \] 标签:Pr,个点,叶子,fer,序列,节点 From: https://www.cnblogs.com/Cnghit/p/17488769.html