BFS
目录 Content
- 概述
- 问题思考与性质
- 典型应用
- 优化与扩展
Part 1 概述
I.什么是BFS?
广度优先搜索(breadth first search),是以同层可达状态优先,一层层向外扩展的搜索算法。一般以队列实现
II.算法基本结构

图源:CSDN @sigd
III.动画过程演示
通常,bfs会用在遍历图,下面的图生动地解释了bfs的过程。

图源:modb.pro @石衫的架构笔记
如图,bfs从初态(树的根节点)一直遍历完整棵树。
算法的过程基本如下:
- 先扩展根节点
- 再依次次扩展与他直接相连的节点
- 重复以上步骤
可以发现,第二步需要保证依次扩展下一层的所有点,为保证不重不漏,我们想到了利用一种数据结构:队列
FBI Warning:有关队列的详细介绍,请到这里食用
队列,是一种允许在队列尾部插入元素,从队列首取出的结构。因此我们称它为“先进先出”的数据结构(FIFO,first in first out).
示意图(OI-Wiki):
C++ STL 为我们提供了方便的队列结构,基础用法:
#include<queue>
using namespace std;
queue<数据类型> 名字;
名字.push(元素) ......插入元素
名字.pop() .......弹出元素
名字.front() ......返回队首元素
名字.empty() .........检查队列是否为空
名字.size() .......元素个数
名字.clear() ........清除队列
这是一点铺垫,剩余请听下回分解
Part 2 问题思考与性质
I.BFS与DFS的区别?
| X | 实现 | 适用场景 | 思想区别 |
|---|---|---|---|
| dfs | 递归 | 一步步确定的问题,有前后依赖性 | 执着往下走,这使得有时dfs可能会有很大损耗(例如:网络流FF) |
| bfs | 队列 | 广泛用于图上,或者可以转换为图的问题 | 一层层考虑,在一般没有分层这个概念时不适用(例如:枚举全排列) |
| 重要:其实 大多数(有例外,视情况而定) 问题dfs、bfs都可以互相转化,只是有一种更优 |
II.BFS有哪些性质?
- 在走地图等问题中,具体来说是每扩展一步代价固定的问题中,第一个bfs到的状态就是最优状态
- 单调性:bfs队列里的节点一定是按层数排序的
- 两段性:bfs队列里至多存在分属于两层的节点
III.BFS有哪些优点
一层层向下考虑,面对状态空间大、状态先后性分明的题目效率高、思考简单。
IV.使用时要注意什么细节
回顾刚刚的结构:
int/void bfs(初始状态){
queue<int> q;
q.push(初态);
vis[初态]=true;//1.根据题目要求检查要不要标记(通常都需要)
while(!q.empty()){
int ln=q.front();q.pop();//2.记住取出状态不然必定死循环
if(找到终点) return 代价;
for(遍历下一层状态){
if(判断是否合法){
vis[新的状态]=true;//3.标记别忘记
q.push(新的状态);
}
}
取消标记或回溯(可能不要)
}
}
这一点最需要注意:
标记问题。
很多人(尤其学了SPFA之后)都搞不清楚到底要不要标记
在这里,可以这么理解:
就像dfs,bfs也有还原现场的步骤,由于要求的最短路不一定每一步代价都一样(不适用于性质1),所以需要回溯来放弃走过的点,以提供其他到达这个点的可能。
Part 3 典型应用
I.走地图问题
小 H 在一个划分成了 \(n \times m\) 个方格的长方形封锁线上。 每次他能向上下左右四个方向移动一格(当然小 H 不可以静止不动), 但不能离开封锁线,否则就被打死了。 刚开始时他有满血 66 点,每移动一格他要消耗 11 点血量。一旦小 H 的血量降到 00, 他将死去。 他可以沿路通过拾取鼠标(什么鬼。。。)来补满血量。只要他走到有鼠标的格子,他不需要任何时间即可拾取。格子上的鼠标可以瞬间补满,所以每次经过这个格子都有鼠标。就算到了某个有鼠标的格子才死去, 他也不能通过拾取鼠标补满 HP。 即使在家门口死去, 他也不能算完成任务回到家中。
地图上有五种格子:
0:障碍物。
1:空地, 小 H 可以自由行走。
2:小 H 出发点, 也是一片空地。
3:小 H 的家。
4:有鼠标在上面的空地。
小 H 能否安全回家?如果能, 最短需要多长时间呢?
这道题非常具有代表性,而且还有一定思维含量。
首先想想,直接套用bfs模版,可以做吗?
不行。首先是血量限制,然后更复杂的是鼠标的限制。
血量限制只需要加一个状态就可以了(用struct)。这个好办
但鼠标为什么会有影响呢?可以看到,题目中说“鼠标是瞬间补充的”,也就是说当一个格子扩展过后不能直接否定它,有可能后面血量不够了还可以回来补充。或者对于一个非鼠标的格子,但是我们必须通过重复走它来拿到鼠标。
如下图所示:(来自题解区@BurningEnderDragon)
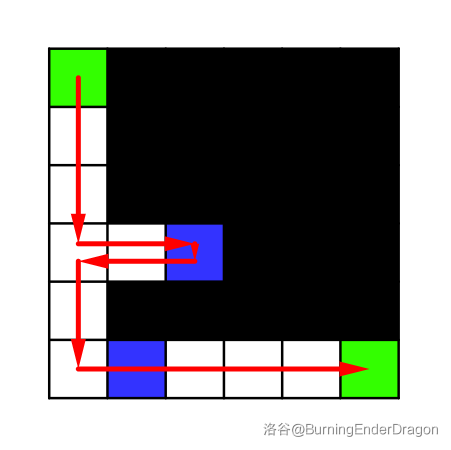
如果我们不重复经过(4,1)(4,2)那么就无法拿到(4,3)的鼠标,此时我们无法到家。
所以重点就是我们如何选择过滤掉重复扩展。这道题中的重复扩展应该是在同一个血量下重复走一个格子。
#include<bits/stdc++.h>
using namespace std;
const int N=10;
int n,m,mp[N][N];
const int dx[4]={0,0,-1,1},dy[4]={-1,1,0,0};
bool vis[N][N][N];
struct node{
int x,y,stp,bld;
};
int bfs(int x,int y){
queue<node> q;
q.push({x,y,0,6});
vis[6][x][y]=1;
while(!q.empty()){
node ln=q.front();q.pop();
if(ln.bld==0) continue;
if(mp[ln.x][ln.y]==3){
return ln.stp;
}
if(mp[ln.x][ln.y]==4){
ln.bld=6;
}
for(int i=0;i<4;i++){
int nx=ln.x+dx[i],ny=ln.y+dy[i];
if(nx<1||nx>n||ny<1||ny>m||vis[ln.bld-1][nx][ny]||mp[nx][ny]==0) continue;
vis[ln.bld-1][nx][ny]=1;
q.push({nx,ny,ln.stp+1,ln.bld-1});
}
}
return -1;
}
int main(){
cin>>n>>m;
int sx,sy;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
if(mp[i][j]==2) sx=i,sy=j;
}
}
int ret=bfs(sx,sy);
cout<<ret;
}
我们通过给vis数组升维来表示血量。
II.洪水填充
例如:
由数字 0 组成的方阵中,有一任意形状闭合圈,闭合圈由数字 1 构成,围圈时只走上下左右 4个方向。现要求把闭合圈内的所有空间都填写成 2。
可以发现,直接找规律非常困难(当时有人写这种做法,居然A了)
我们可以从地图外开始遍历,就像洪水一样填充外圈,闭合的圈就像墙一样挡住了洪水。
III.最短路
<1.方格图最短路>
特殊的最短路,走一步的代价通常为1或定值
这样就可以利用BFS的性质快速解。
<2.SPFA>
借助BFS思想实现的简单实用的最短路算法。
void spfa(int s){
queue<int> q;
q.push(s);
vis[s]=true;
while(!q.empty()){
int ln=q.front();q.pop();
vis[ln]=false;
for(int i=head[ln];i;i=e[i].next){
if(dist[ln]+e[i].w<dist[e[i].v]){
dist[e[i].v]=dist[ln]+e[i].w;
if(!vis[e[i].v]){
vis[e[i].v]=true;
q.push(e[i].v);
}
}
}
}
return;
}
由于要求最短路,所以此时vis数组的含义应该是“是否在队列中”而松弛操作是可以随时进行的,vis的意义仅仅是防止无意义的入队。
时间复杂度通常很快。但是遇见方格图、菊花图时效率会退化。如果是正权图建议用Dij-Heap,带负权就放心用spfa。(详细的以后讲)
Part 4 优化与扩展
I.双端队列BFS
其实与普通BFS结构相差无几:
int/void bfs(初始状态){
deque<int> q;
q.push_back(初态);
vis[初态]=true;//1.根据题目要求检查要不要标记(通常都需要)
while(!q.empty()){
int ln=q.front();q.pop_front();//2.记住取出状态不然必定死循环
if(找到终点) return 代价;
for(遍历下一层状态){
if(判断是否合法){
vis[新的状态]=true;//3.标记别忘记
if(权值==0)
q.push_back(新的状态);
else
q.push_front(新的状态);
}
}
取消标记或回溯(可能不要)
}
}
其中,deque是双端队列,它可以在队列两头进行操作。
我们重点注意以下片段:
if(权值==0)
q.push_back(新的状态);
else
q.push_front(新的状态);
上面说过,bfs队列应该满足单调性,为什么我们在这里可以在队头插入呢?
其实是一种贪心的思想。分类讨论:如果要求最大权值
- 若新的点权值为0:那么它就没有权值为1的点好,于是可以把它放到后面
- 反之,放到前面提高效率。
这种方法适用于权值有2种的情况
II.优先队列BFS
同 I,只是deque换成了priority_queue(不了解的请OI-Wiki之)
III.双向BFS
可以同时使用2个队列,从终态初态一起开始搜索,直到他们产生交汇为止。
可以使得复杂度缩小一半。
典例 Nightmare II
给定一张 N×M 的地图,地图中有 1 个男孩,1 个女孩和 2 个鬼。
字符 . 表示道路,字符 X 表示墙,字符 M 表示男孩的位置,字符 G 表示女孩的位置,字符 Z 表示鬼的位置。
男孩每秒可以移动 3 个单位距离,女孩每秒可以移动 1 个单位距离,男孩和女孩只能朝上下左右四个方向移动。
每个鬼占据的区域每秒可以向四周扩张 2 个单位距离,并且无视墙的阻挡,也就是在第 k 秒后所有与鬼的曼哈顿距离不超过 2k 的位置都会被鬼占领。
注意: 每一秒鬼会先扩展,扩展完毕后男孩和女孩才可以移动。
求在不进入鬼的占领区的前提下,男孩和女孩能否会合,若能会合,求出最短会合时间。
笔记
设有点A(x,y),B(a,b)则A、B的曼哈顿距离为\(\lvert x-y \lvert +\lvert a-b\lvert\)
可以从男孩和女孩一起开始搜索。
P.S 因代码遗失,此处放的是@垫底抽风(Acwing)的题解:
#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
const short dx[4] = {0, 1, 0, -1}; // 四个方向
const short dy[4] = {1, 0, -1, 0};
const short N = 805; // 地图大小上限
// 结构体存 男孩/女孩/鬼,(当然鬼也可以用pair)
// (x, y) 表示其坐标位置,s 表示到达该点的距离。
struct Point{short x, y, s;};
short n, m; // 地图大小
bool g[N][N]; // 存地图。true 表示能走,false 表示不能走
short st[N][N]; // 存每个点的状态。没被到过是 0,被男孩到过是 1,被女孩到过是 2
Point ghost[2]; // 存两个鬼的坐标
// 返回 a - b 的绝对值(当然也可以用 abs 写)
short sub(short a, short b)
{
return a > b ? a - b : b - a;
}
// 判断 (x, y) 在第 t 秒的时候是否被某个鬼占领
bool check(short x, short y, short t)
{
// 枚举两个鬼,如果某个鬼到 (x, y) 的曼哈顿距离 < 2t 那么返回 false
for (short i = 0; i < 2; i ++ )
if (sub(ghost[i].x, x) + sub(ghost[i].y, y) <= t << 1)
return false;
return true; // 否则说明没有鬼占领,放回 true
}
// 扩展队列 q 中所有到初始点距离在 v * t 以下的点
// 其中 t 是时间,v 是速度
bool BFS(queue<Point> &q, short t, short v)
{
// 只要 q 不空,并且队头元素到初始点的距离小于 v * t,就继续扩展
while (q.size() && q.front().s < t * v)
{
Point u = q.front(); q.pop(); // 先取出队头
if (!check(u.x, u.y, t)) continue; // 如果队头元素已经被鬼占领(好惨),则跳过
for (short i = 0; i < 4; i ++ ) // 枚举四个方向进行扩展
{
short a = u.x + dx[i], b = u.y + dy[i]; // 求出按该方向移动一格后的坐标
// 如果该坐标在地图内,且能走,且没被鬼占领
if (~a && ~b && a < n && b < m && g[a][b] && check(a, b, t))
if (!st[a][b]) // 如果该位置没被遍历过
{
// 记录该位置被遍历过。
// st[u.x][u.y] 是被谁遍历的,则 st[a][b] 就是被谁遍历过的。
st[a][b] = st[u.x][u.y];
// 将该点加入队列中
q.push({a, b, u.s + 1});
}
// 如果遍历 (a, b) 的和遍历 (u.x, u.y) 的不是一个人,说明男女会合了,返回 true
else if (st[a][b] != st[u.x][u.y]) return true;
}
}
return false; // 男女没会合,返回 false
}
// 求出男女会合的最短时间。如果不能会合,返回 -1
short bfs(Point boy, Point girl)
{
memset(st, 0, sizeof st); // 将 st 初始化为 0
// q_boy 是男孩的 bfs 队列,q_girl 是女孩的 bfs 队列
queue<Point> q_boy, q_girl;
// 分别将男孩和女孩加入队列中
q_boy.push(boy), q_girl.push(girl);
// 男孩到的点标记为 1,女孩到的点标记为 2
st[boy.x][boy.y] = 1, st[girl.x][girl.y] = 2;
// 按时间从 1 开始枚举。只要有一个队列没空,就继续枚举。
for (short t = 1; q_boy.size() || q_girl.size(); t ++ )
if (BFS(q_boy, t, 3) || BFS(q_girl, t, 1)) // 男孩速度为 3,女孩速度为 1
return t; // 如果在扩展男孩或者扩展女孩时扩展到了对方,那么直接返回 t
return -1; // 跳出循环说明两个队列都空了,返回 -1
}
int main()
{
short test;
scanf("%hd", &test);
while (test -- ) // 注意多组测试数据qwq
{
scanf("%hd%hd\n", &n, &m);
Point boy, girl;
// 读入地图。i 和 j 分别枚举行列,cnt 枚举当前读入到了第几个鬼
for (short i = 0, cnt = 0; i < n; i ++ , getchar())
for (short j = 0; j < m; j ++ )
{
char ch = getchar();
if (ch == 'M') boy = {i, j, 0}; // 如果该字符为 'M',说明是男孩,存入 boy
else if (ch == 'G') girl = {i, j, 0}; // 如果该字符为 'G',说明是女孩,存入 girl
else if (ch == 'Z') ghost[cnt ++ ] = {i, j, 0}; // 该字符是 'Z',说明是鬼,存入 ghost
g[i][j] = ch != 'X'; // 如果该字符不为 'X',则该位置能走
}
printf("%d\n", bfs(boy, girl)); // 输出 bfs 的结果即可
}
return 0;
}
//作者:垫底抽风
//链接:https://www.acwing.com/solution/content/16498/
//来源:AcWing
//著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
EOF
感谢观看。\(\huge{QwQ}\)
标签:bfs,short,ln,int,BFS,队列,关于 From: https://www.cnblogs.com/haozexu/p/17488417.html