关于最小生成树

目录

• 概述
• 性质
• Prim 算法

• 实现
• 例 P1194 买礼物

• Kruskal算法

• 实现
• 思想
• 例 P4047 部落划分

Part 1 概述

一个连通图的生成树是一个极小的连通子图，它包含图中全部的n个顶点，但只有构成一棵树的n-1条边。

我们定义无向连通图的最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树。

通常解决这两个问题有两种算法，同最短路问题一样，这两种算法也分别是基于选择点和选择边。但是其实他们都使用了贪心的思想。

Part 2 性质

• 一个连通图可以有多个生成树；
• 一个连通图的所有生成树都包含相同的顶点个数和边数；
• 生成树当中不存在环；
• 移除生成树中的任意一条边都会导致图的不连通， 生成树的边最少特性；
• 在生成树中添加一条边会构成环。
• 对于包含n个顶点的连通图，生成树包含n个顶点和n-1条边；
• 对于包含n个顶点的无向完全图最多包含\(n^{n-2}\)颗生成树。

Part 3 Prim

• 实现

每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。这个距离也可以称为“到生成树的距离”。

其实跟 Dijkstra 算法一样，每次找到距离最小的一个点，可以暴力找也可以用堆维护。

• 从任意一个结点开始，将结点分成两类：已加入的，未加入的。

• 每次从未加入的结点中，找一个与已加入的结点之间边权最小值最小的结点。

• 然后将这个结点加入，并连上那条边权最小的边。

• 重复n-1次即可。

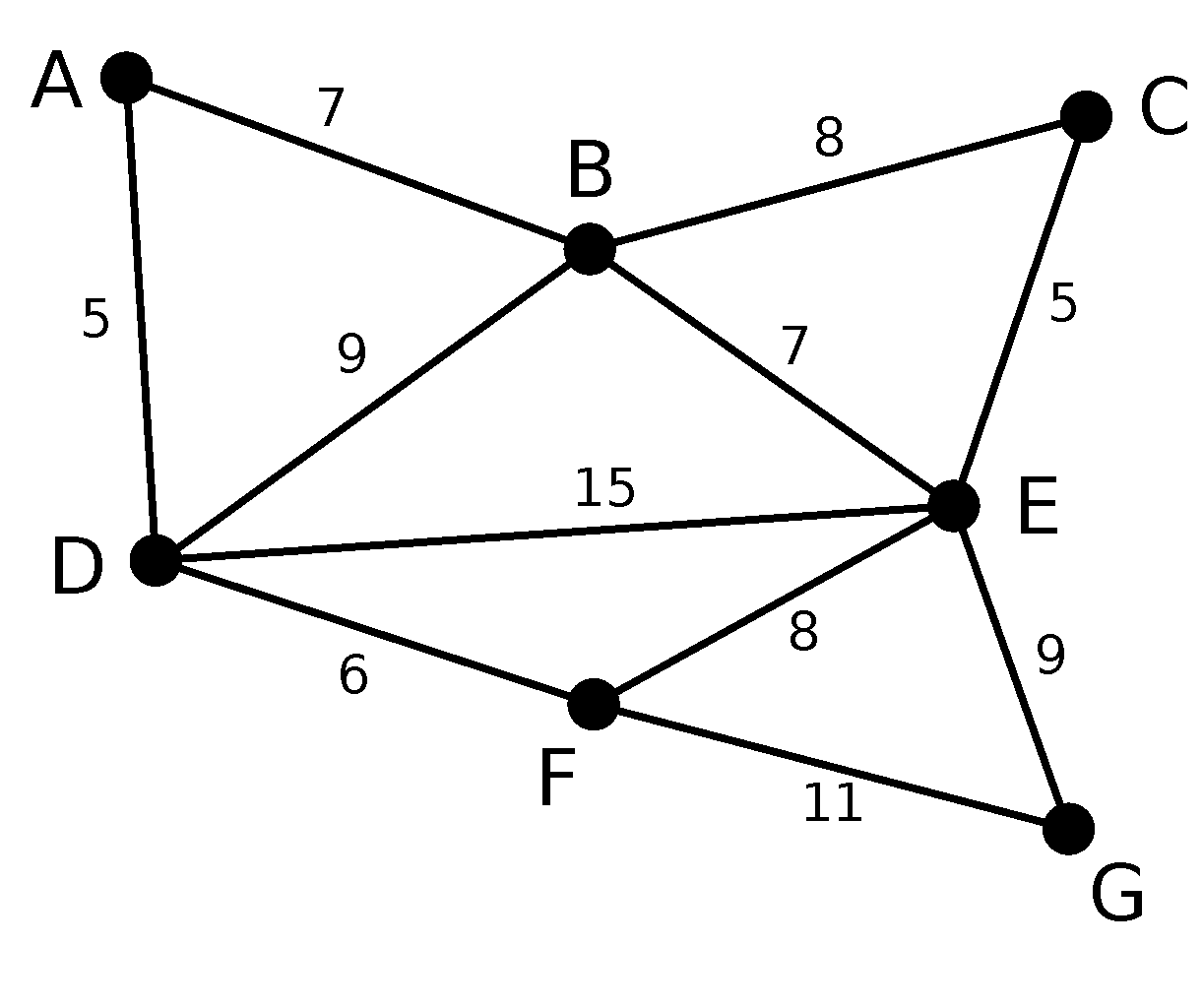
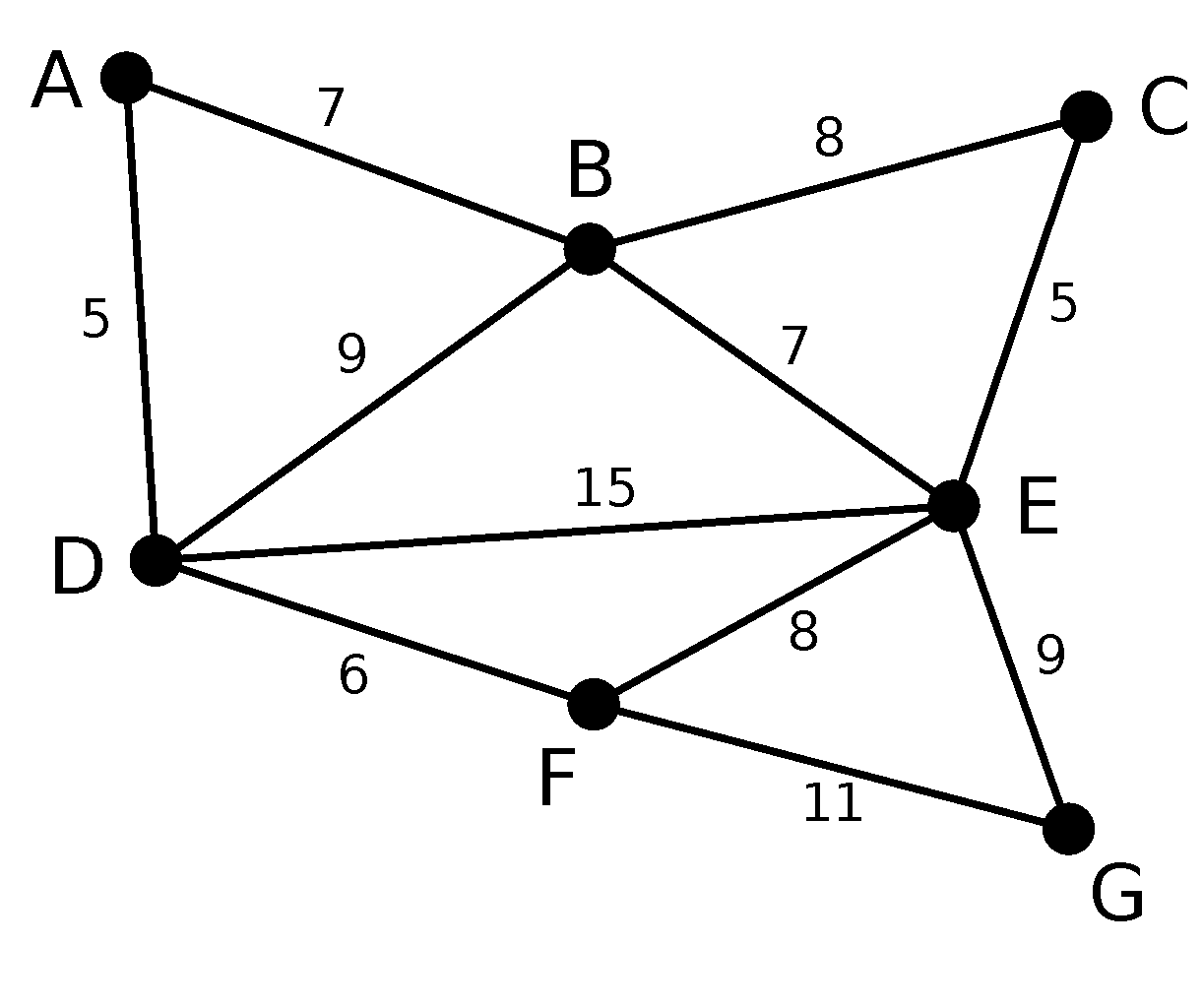
图示，图源OI-WIKI

int n,m,ans;
vector< pair<int,int> > mp[5005];
int dist[5005];
bool vis[5005],falg=true;
void prim()
{
	memset(dist,0x3f,sizeof(dist));
//	vis[temp]=true;
    dist[1]=0;
	for(int i=1;i<=n;i++)
	{
		int mins=0x3f3f3f3f,newn=-1;
		for(int j=1;j<=n;j++)
		{
			if(!vis[j]&&mins>dist[j])
			{
				mins=dist[j];
				newn=j;
			}
		}
		if(newn==-1)
		{
			falg=false;
			return;
		}
		vis[newn]=true;
		ans+=mins;
		for(int j=0;j<mp[newn].size();j++)
		{
			if(vis[mp[newn][j].first]) continue;
			if(dist[mp[newn][j].first]>mp[newn][j].second) dist[mp[newn][j].first]=mp[newn][j].second;
		}
	}
	return;
}

• 例题 买礼物
  其实，prim没有什么特别的用法，理解上也不如下面那种简单。但是当时我用的是这种方法做这个题，所以就用这个来讲。恰好这个问题也比较有意思。

题目描述

又到了一年一度的明明生日了，明明想要买 \(B\) 样东西，巧的是，这 \(B\) 样东西价格都是 \(A\) 元。

但是，商店老板说最近有促销活动，也就是：

如果你买了第 \(I\) 样东西，再买第 \(J\) 样，那么就可以只花 \(K_{I,J}\) 元，更巧的是，\(K_{I,J}\) 竟然等于 \(K_{J,I}\)。

现在明明想知道，他最少要花多少钱。

也就是说，这些物品的关系中有依赖性。所以我们可以建图来表达这种关系。

具体来说，第i件物品对j有优惠的话就建边（边权\(K_{i,j}\)），然后从0向各点连边权为a的边（因为买i需要a元）

那么，如果要买所以东西，那么就需要把所有的点包起来，由于每一个东西都只要付钱一次，所以，我们的选择就会构成一棵生成树。

代码:

#include<bits/stdc++.h>
using namespace std;
int a,b,mp[505][505],ans,minans=0x3f3f3f3f;
int dist[505];
bool vis[505];
void prim(int s)
{
	memset(vis,false,sizeof(vis));
	memset(dist,0x3f,sizeof(dist));
	dist[s]=0;
	ans+=mp[s][s];
	for(int k=1;k<=b;k++)
	{
		int mins=0x3f3f3f3f,id=-1;
		for(int i=1;i<=b;i++)
		{
			if(!vis[i]&&dist[i]<mins)
			{
				mins=dist[i];
				id=i;
			}
		}
		if(id==-1) return;
		vis[id]=true;
		ans+=mins;
		for(int i=1;i<=b;i++)
		{
			if(vis[i]||mp[id][i]==0x3f3f3f3f) continue;
			if(dist[i]>mp[id][i]) dist[i]=mp[id][i];
		}
	}
}
int main()
{
	cin>>a>>b;
	memset(mp,0x3f,sizeof(mp));
	int g;
	for(int i=1;i<=b;i++)
	{
		for(int j=1;j<=b;j++)
		{
			cin>>g;
			mp[i][j]=g;
			if(mp[i][j]==0) mp[i][j]=a;
			if(g>a) mp[i][j]=a;
		}
	}
	for(int i=1;i<=b;i++)
	{
		ans=0;
		prim(i);
		minans=min(minans,ans);
		//cout<<ans<<endl;
	}
	cout<<minans;
}

Part 4 Kruskal

• 实现

过程:

• 从小到大排序边

• 顺序遍历边，如果两边不在MST上，那么把该边加入MST

• 直到加入n-1条边

• 思想

其实Kruskal与Prim一样都是使用贪心的思想，只不过Kruskal是贪边。

当我们尝试加入另一条边的时候，我们要考虑它的两个端点是不是已经在MST上了，否则这条边的加入不仅没有连接新的点，还让MST上形成了环，不满足生成树的定义。

那么贪心是应该如何思考呢？

不妨将问题拆开，设MST是\(T\)，当前已经选择的边集是\(F\)，已经选择的点集是\(N\)，接下来要选的边是\(e(i \to j)\)

分情况讨论：

• 如果\(i \in N \text{且} j \in N\)，那么选择该边并没有使得MST扩张，反而使得MST上产生环，不选。
• 如果\(i \in N \text{且} j \not \in N\)，那么：

假设还有一条边\(f\)满足\(f:i \to j \text{且} f \not\in F\)那么选择它的权肯定比\(e\)大，否则就会先选。

再考虑还有若干条边使得\(i\to k\to j\)那么他们的权值肯定都大于\(e\)否则就会先选它们。

• 如果\(i \not\in N \text{且} j \not \in N\)，那么：之后如果要找到MST肯定要通过某种方式连接，但由于顺序遍历，之后再连接，肯定不如现在的了。

综上所述，此时选\(e\)肯定最优。

（仅自我理解欢迎批评）

图示：OI-Wiki图

如图所示，依次考虑边，绿色的是可以选的，红色是选不了的。

• 例 部落划分

聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。

不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了 nn 个野人居住的地点（可以看作是平面上的坐标）。我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了 kk 个部落！这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法：

对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。

我们把每个点看成一个部落，每次取最小距离的两个抱团，同时部落也减少了一个....然后直到部落数==目标数，此时下一个不同部落的距离就是最短的距离。

代码：

#include<bits/stdc++.h>
using namespace std;
struct edge
{
	int u,v;
	double w;
}mp[500005];
struct node
{
	int x,y;
}s[1005];
double ED(int i,int j)
{
	return double(sqrt(double(pow(double(s[i].x-s[j].x),2))+double(double(pow(double(s[i].y-s[j].y),2)))));
}
int n,k,m;
double ans;
int fa[1005];
bool cmp(edge a,edge b)
{
	return a.w<b.w;
}
int find(int x){
	return fa[x]==x?fa[x]:fa[x]=find(fa[x]);
}
double kruskal()
{
	int cnt=0;
	for(int i=1;i<=m;i++)
	{
		if(find(mp[i].u)!=find(mp[i].v))
		{
		//	ans+=mp[i].w;
			fa[fa[mp[i].u]]=fa[mp[i].v];
			cnt++;
			if(cnt>=n-k) 
			{
			break;//To-Do
			}
	}
}
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>s[i].x>>s[i].y;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=i+1;j<=n;j++)
		{
			m++;
			mp[m].u=i;
			mp[m].v=j;
			mp[m].w=ED(i,j);
		}
	}
	for(int i=1;i<=n;i++) fa[i]=i;
	sort(mp+1,mp+m+1,cmp);
	kruskal();
	ans=99999999;
	for(int i=1;i<=m;i++)
	{
		if(find(mp[i].u)!=find(mp[i].v))
		{
			ans=min(ans,mp[i].w);
		}
	}
	printf("%.2lf",ans);
	return 0;
}