FFT 学习笔记

首先就是中考这几天我们学校做考场，然后初二放假在家写作业。

然后我就摸鱼来推之前不会的 FFT 的式子，推一推发现诶麻麻我懂了！麻麻我悟了麻麻！

于是在放假第二天我写下了这样一篇学习笔记 qwq

多项式的系数表示和点值表示

我们都知道，一个 \(n\) 项多项式，如果我们写成一个函数，就可以写成这样：

\(f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \dots + a_{n - 1}x^{n - 1}\)

如果我们有两个 \(n\) 项的多项式 \(f\) 与 \(g\)，然后我们想要算它们俩的乘积应该怎么办呢？似乎我们只能 \(O(n^2)\)。

我们都知道，两点确定一个一次函数，三点确定一个二次函数，推广开来，\(n\) 个点可以确定一个 \(n\) 项的多项式。如果我们取出了 \(n\) 个横坐标 \(\{x_1, x_2, \dots, x_n\}\)，然后我们算出来了 \(f\) 与 \(g\) 它们对应的横坐标的点集，\(\{(x_1, f(x_1)), (x_2, f(x_2)), \dots, (x_n, f(x_n))\}\) 和 \(\{(x_1, g(x_1)), (x_2, g(x_2)), \dots, (x_n, g(x_n))\}\)

横坐标不变，纵坐标相乘，得到新的 \(n\) 个点 \(\{(x_1, f(x_1)g(x_1)), (x_2, f(x_2)g(x_2)), \dots, (x_n, f(x_n)g(x_n))\}\) 这 \(n\) 个点一定在 \(f\) 与 \(g\) 的乘积的函数上。

这是相当好理解的。由于 \(n\) 点确定一个 \(n\) 项式，事实上我们已经知道了 \(f\) 乘 \(g\) 对不对？时间复杂度就是刚刚的相乘，也就是 \(O(n)\)。

快去开香槟！但事实上我们求点的复杂度为 \(O(n^2)\)。由于正常人都不会用 \(n\) 个点表示一个 \(n\) 项式，所以我们还要把这 \(n\) 个点转化成系数表达法才行，然后就要用高斯消元，时间复杂度 \(O(n^3)\)。

那我还不如暴力对吧，但是，事实上这给了我们启发，有没有一种方法能够取一些非常厉害的 \(x\)，能让我们加速求出 \(n\) 个对应点的纵坐标（这叫插值）和加速求出系数（这叫还原） 呢？

这就有了傅里叶变换了~

一些前置知识

虚数和复数

1 虚数

我们定义 \(i = \sqrt{-1}\)，\(i\) 就是虚数单位。你可能会像曾经的我一样纠结于 \(i\) 是啥啊它是啥数啊它究竟是什么啊 QAQ 之类的问题。但是事实上 \(i\) 啥都不是，反正就是个符号（

2 复数

这可不是我们说的负数，而是复数，就是一个实数和一个虚数构成，一般用 \(z\) 表示，记为 \(z = a + bi\)，其中 \(a\) 为实数，叫 \(z\) 的实部，\(bi\) 为虚数，叫 \(z\) 的虚部。

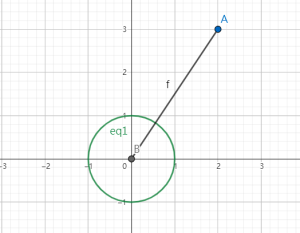
值得一提的是，\(z\) 可以在平面直角坐标系上用向量清晰地刻画出来。如图，从源点到点 \((2, 3)\) 构成一个向量，这条向量就代表复数 \(z = 2+3i\)。这里的纵轴叫虚轴（纵坐标代表虚部的 \(b\)），横轴叫实轴（横坐标代表实部的 \(a\)）

3 单位圆和单位根

在上图突兀的闯入了一个以原点为圆心，\(1\) 为半径的圆，这个圆很厉害，它的名字叫单位圆。单位圆有什么用呢？如果我们将单位圆 \(n\) 等分，画出 \(n\) 条半径，它们所对应的复数是 \(x^n = 1\) 的一个复数根。

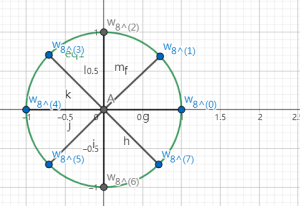
比如这张图 \(n = 8\)（其实我标点的时候想标成 \(w_n^k\) 但是这个只能给我标成这个样子，大家凑合看吧 qwq）

从 \((1, 0)\) 开始将单位圆平分成 \(8\) 等分，有 \(8\) 条半径，从 \(0\) 开始逆时针编号，一直到 \(n - 1\)。每一个半径都对应着一个复数，我们记第 \(k\) 条半径的这个复数为 \(w_n^k\)，很显然，\(w_n^0 = 1\)。其中 \((w_n^k)^n = 1\)，具体而言我不会证（

然后呢？由于我们学过三角函数，我们容易得到 \(w_n^k = \cos(2\pi k/n) + i \sin(2\pi k / n)\)。同时还有 \(w_n^k = (w_n^1) ^k\)，也就是说这个 \(k\) 可以看成 \(w_n^1\) 的指数，而不仅仅是一个上标（这条我也不会证，我太菜了 QAQ）

4 单位根的性质

1. 折半定理
   \(w_n^k = w_{2n}^{2k}\)。
   相信大家看看上面的图就懂了。如果喜欢理性荔枝地证明的话——
   \(w_n^k = \cos(2\pi k / n) + i \sin(2\pi k / n)\\ = \cos(2\pi (2k / 2n)) + i \sin(2\pi(2k / 2n)) \\ = w_{2n}^{2k}\)

2. 消去定理
   \(w_n ^k = -w_n ^{k - n / 2}\)（\(n\) 是偶数，\(k \le n / 2\))。
   一看图相信大家都明白啦，因为它俩关于原点对称，等大反向。

相信这些对大家都不难！了解了这些，FFT 就很容易啦~

FFT

插值

FFT 是用分治做的，所以下面我们默认 \(n\) 为 \(2\) 的整数次幂。

FFT 的精华在于倒式子，这个式子虽然很长，但是很好理解，相信大家都能看懂！ヾ(◍°∇°◍)ﾉﾞ

\(f(x) = a_0 + a_1x + a_2x^2 + \dots a_{n - 1}x^{n - 1} \\ = (a_0 + a_2x_2 + a_4x_4 + \dots a_{n - 1}x^{n - 1}) + \\ (a_1x+ a_3x^3 + a_5x^5 + \dots a_{n - 2}x^{n - 2})\)

这一步是将下标按照奇偶性分类。我们定睛一看，发现这两边很相似，很漂亮，为了化简我们新定义两个函数

\(A_1(x) = a_0 + a_2x + a_4x^2 + \dots + a_{n - 1}x^{(n - 1) / 2}\)
\(A_2(x) = a_1 + a_3x + a_5x^2 + \dots + a_{n - 1}x^{(n - 1) / 2 - 1}\)
然后 \(f(x) = A_1(x^2) + xA_2(x^2)\)

FFT 最巧妙的一步在于，它代入的是 \(n\) 的单位根们，\(w_n^1, w_n^2, \dots w_n^{n - 1}\)。

所以就有 \(f(w_n^k) = A_1((w_n ^ k) ^ 2) + w_n ^ k A_2((w_n ^ k) ^ 2) \\ = A_1(w_n^{2k}) + w_{n}^k A_2(w_n^{2k})\)

第三步是因为 \(w_n ^k\) 的上标可以看成 \(w_n ^1\) 的指数

下面简单的分讨一下。

对于 \(k \le n / 2\)，\(f(w_n^k) = A_1(w_n^{2k}) + w_{n}^k A_2(w_n^{2k}) \\ = A_1(w_{n / 2}^k) + w_n^kA_2(w_{n / 2}^k)\)。这是因为折半定理

对于 \(k > n / 2\)，\(w_n^k = -w_{n} ^{k - n / 2}\)，两边同时平方一下就有了 \(w_n^{2k} = w_n^{2k-n}\)，再用折半定理，就能得到 \(w_{n / 2} ^k = w_{n / 2} ^{k - n / 2}\)。

所以呢 \(f(w_n^k) = A_1(w_n^{2k}) + w_{n}^k A_2(w_n^{2k}) \\ = A_1(w_{n / 2}^k) + w_n^kA_2(w_{n / 2}^k) \\ = A_1(w_{n / 2}^{k - n / 2}) - w_n^{k - n /2 }A_2(w_{n / 2}^{k - n / 2})\)。

\(k - n / 2 < n / 2\)，诶这个问题我刚刚不解决过了嘛！

所以我们就可以分治，先分治处理 \(A_1\)，再分治处理 \(A_2\)，然后就是按照上面的式子合并 \(A_1, A_2\)，最后我们就可以得到啦~

时间复杂度是经典的 \(T(n) = 2T(n / 2) + n\)，也就是 \(O(n\log_2 n)\)

那么怎么点值转系数呢？

下面要简单的做一个小推导 qwq

比如多项式 \(f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \dots + a_{n - 1}x^{n - 1}\)，我们刚刚傅里叶变换出来了 \(\{f(w_n^0), f(w_n ^ 1), \dots, f(w_n ^ {n - 1})\}\)，我们记它们为 \(\{b_0, b_1, b_2, \dots, b_{n - 1}\}\)。

然后我们新构造一个多项式 \(g(x) = b_0 + b_1x + b_2x^2 + b_3x^3 + \dots + b_{n - 1}x^{n - 1}\)，然后我们将 \(w_n^k\) 的倒数 \(w_n^{-k}\) 弄出来代入得到 \(\{g(w_n^0), g(w_n ^ {-1}), \dots, g(w_n ^ {1-n})\}\)（这些倒数很显然满足折半和消去定理），我们记它为 \(\{c_0, c_1, c_2, \dots, c_{n - 1}\}\)。傅里叶：有完没完啊啊啊啊啊

然后我们开始推导 $c_k = g(w_{n}^{-k}) = \sum\limits_{i = 0}^{n - 1}b_i w_{n}^{-ik} \ = \sum\limits_{i = 0}^{n - 1}((\sum\limits_{j= 0}^{n - 1}a_j w_n ^ {ij})w_{n}^{-ik}) \ = \sum\limits_{i = 0}^{n - 1}(\sum\limits_{j= 0}^{n - 1}a_j w_n ^ {(j - k)i}) \ = \sum\limits_{j = 0}^{n - 1} a_j(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i}) $

当 \(j = k\) 时，\(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i} = \sum\limits_{i= 0}^{n - 1}w_n ^ 0 = n\)

当 \(j \not = k\) 时，\(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i}\) 这一坨实际上是一个首项为 \(1\)，公比为 \(w_{n}^{j - k}\) 的等比数列！

所以 \(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i}) = \dfrac{w_n^{n(j - k)} - 1}{w_n^{j - k} - 1} = \dfrac{1^{(j - k)} - 1}{w_n^{j - k} - 1} = 0\)

所以 \(c_k = na_k\)，即 \(a_k = \dfrac{c_k}{n}\)。

等等！我们似乎找到了系数和点值的关系！

这就是 FFT 还原的方法

先对 \(f\) 做一遍插值，再用插值得到的点值为系数，构造一个新的多项式 \(g\)，代入单位根的倒数 \(w_n^0, w_n^{-1}, \dots, w_n^{1 - n}\) 到 \(g\) 里面去，再做一遍插值。所得的点值除以 \(n\) 就是 \(f\) 的各项系数。

还有优化，明天填坑 qwq