什么是动态规划?
动态规划 \((\mathbb{D}ynamic~\mathbb{P}rograming)\)算法是解决 \(\color{red}多阶段决策过程最优\) 的通用方法。在这类问题中,可能有多个可行解。每一个解都对应着一个值,而我们希望找到的是 \(\color{red}最优值的解\)。
要了解动态规划的概念,首先要知道什么是 \(\color{red}多阶段决策问题\)。
多阶段决策问题
如果一类活动过程可以分为 \(\color{red}若干个相互联系的阶段\) ,在每一个阶段都需\(\color{red}做出决策\)(采取措施),一个阶段的决策确定以后,常常影响到下一个阶段的决策,从而就完全地确定了一个过程的活动路线,则称它为\(\color{red}多阶段决策问题\)。
策略
各个阶段的决策构成一个\(\color{red}决策序列\),称为一个\(\color{red}策略\)。每一个阶段都有若干个决策可供选择,因而就有许多策略供我们选取,对应于一个策略可以确定活动的效果,这个效果可以用数量来确定。策略不同,效果也会有所不同。多阶段决策问题,就是要在可以选择的策略之间,\(\color{red}选取一个最优策略,使在预定的标准下达到最好的效果\)。
举个例子:最短路径问题求解
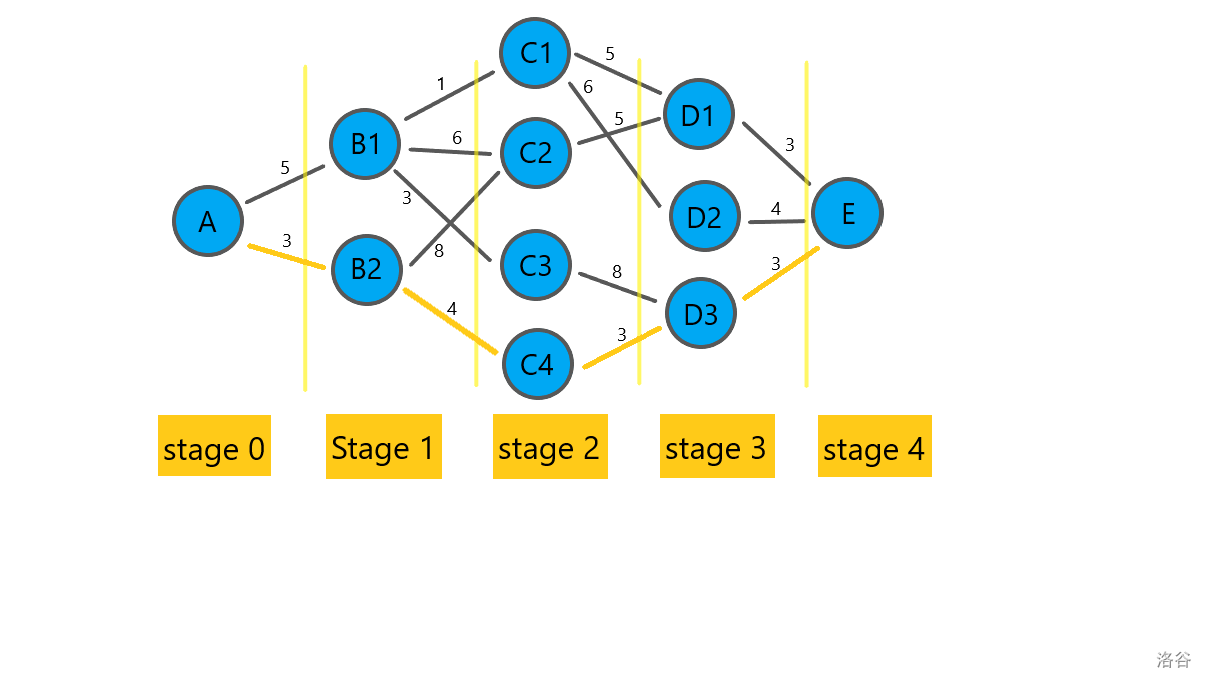
求 \(A\) 到达 \(E\) 的最短距离。
思考:仔细观察本图路径的特殊性,可以分成四个阶段。第一阶段\((Stage~1)\) :
\(A\) 有两条通路:\(A \to B_1\) 和 \(A \to B_2\);第二阶段\((Stage~2)\) :
\(B_1\) 有三条通路:\(B_1 \to C_1\) , \(B_1 \to C_2\) , \(B_1 \to C_3\);
\(B_2\) 有两条通路:\(B_2 \to C_2\) , \(B_2 \to C_4\);第三阶段\((Stage~1)\) :
\(C_1\) 有两条通路:\(C_1 \to D_1\) 和 \(C_1 \to D_2\);
\(C_2\) 有一条通路:\(C_2 \to D_1\);
\(C_3\) 有一条通路:\(C_3 \to D_3\);
\(C_4\) 有一条通路:\(C_4 \to D_3\);第四阶段\((Stage~1)\) : \(D_1\) 有一条通路:\(D_1 \to E\);
\(D_2\) 有一条通路:\(D_1 \to E\);
\(D_3\) 有一条通路:\(D_1 \to E\).解决方法:倒着推 (设 \(F(x)\) 表示 \(x\) 点到 \(E\) 点的最短路径的长度)
不难想到:\(\color{red}F(x) = min\{所有x点指向的点y之间的路径长度 + F(y)\}\)
名词解释: 我们把 \(F(x)\) 称为当前\(\color{red}x~的状态\);每一的阶段的选择\(\color{red}依赖于\)当前的状态,又随即\(\color{red}引起状态的转移\);一个决策序列\(\color{blue}\{E\to D_3\to C_4\to B_2\to A\}\)就是在\(\color{red}变化的状态\)中产生的,故有\(\color{red}“动态”\)的含义。
小结
| 三个基本的概念 |
|---|
| 1.\(\color{red}阶段\): 问题的过程被分成若干个相互联系的部分,我们称之为阶段,以便按一定的次序求解。 |
| 2.\(\color{red}状态\): 某一阶段的出发位置称为状态,通常一个阶段包含着若干个状态。 |
| 3.\(\color{red}决策\): 对问题的处理中做出的每种选择的行动就是决策。即从该阶段的每个状态出发,通过一次选择性的行动移至下一个阶段的相应状态。 |