1. \(\operatorname{Kruskal}\) 最小生成树
本来觉得这个没必要写但是强迫症发作只能写了qwq
真实原因是我居然交了四发才过板子题可以说是人类之耻了
\(\operatorname{Kruskal}\) 算法需要先把边按照权值进行排序,用贪心的思想优先选取权值较小的边,并依次连接
若出现环则跳过此边(用并查集来判断是否存在环)继续搜,直到已经使用的边的数量比总点数少一即可
否则将两个不同的并查集合并
看个动图就能理解了(绿边表示已选,红边表示不可选)
考虑模板
点击查看代码
#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<algorithm>
#define WR WinterRain
#define int long long
using namespace std;
const int WR=1001000,mod=993244853;
struct Edge{
int frm,to,val;
bool operator<(const Edge&b)const{
return val<b.val;
}
}edge[WR<<1];
int n,m;
int tot,ans;
int fa[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<1)+(s<<3)+ch-'0';
ch=getchar();
}
return s*w;
}
void add(int u,int v,int val){
edge[++tot].frm=u;
edge[tot].to=v;
edge[tot].val=val;
}
int getfa(int x){
if(fa[x]==x) return x;
return fa[x]=getfa(fa[x]);
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++){
int u=read(),v=read(),val=read();
add(u,v,val);add(v,u,val);
}
sort(edge+1,edge+1+tot);
for(int i=1;i<=tot;i++){
int u=edge[i].frm,v=edge[i].to,val=edge[i].val;
int fau=getfa(u),fav=getfa(v);
if(fau==fav) continue;
fa[fau]=fav;
ans+=val;
}
for(int i=2;i<=n;i++){
if(getfa(i)!=fa[1]){
printf("orz\n");
return 0;
}
}
printf("%lld\n",ans);
return 0;
}
然后我们考虑
2. \(\operatorname{Kruskal}\) 重构树
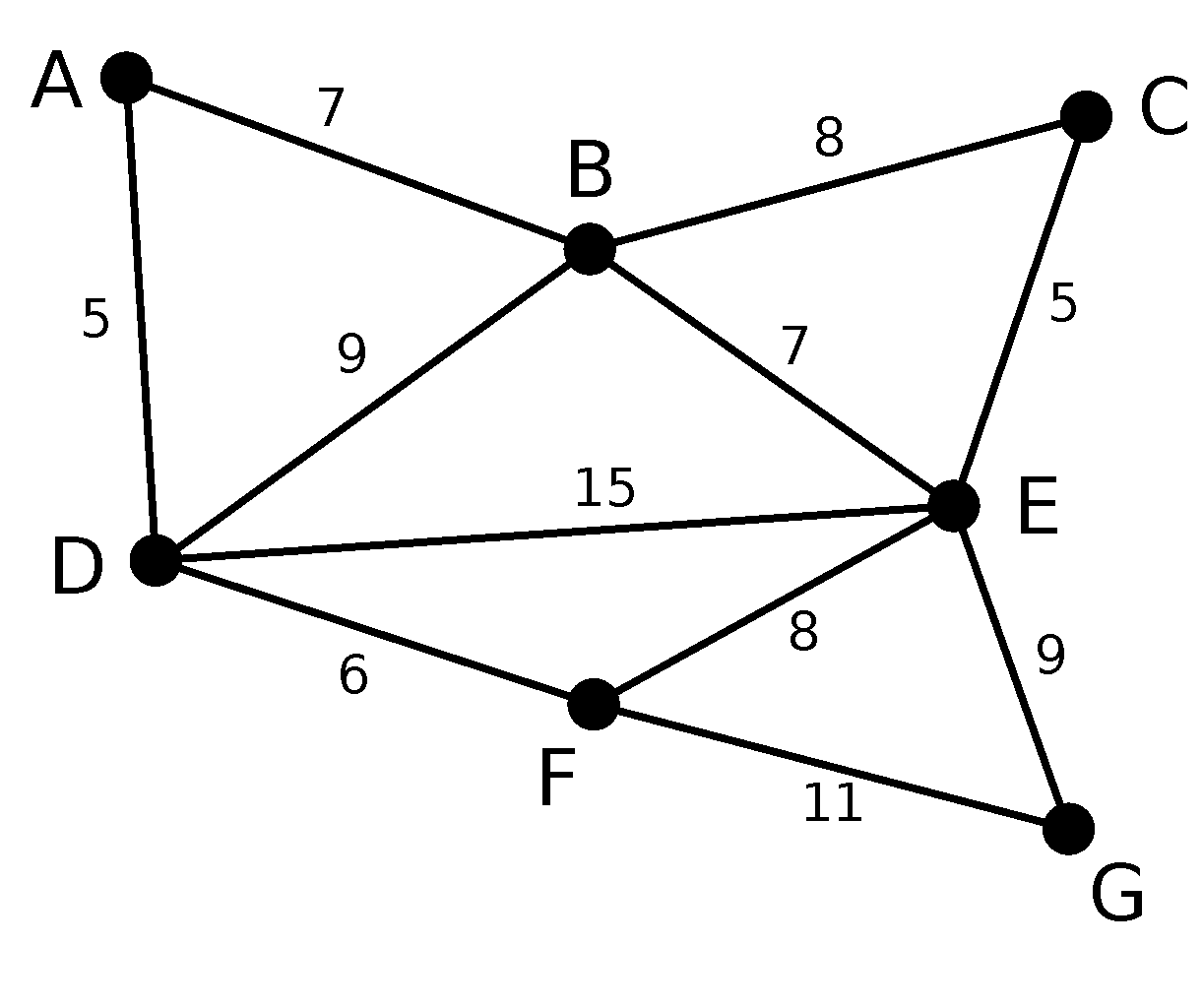
考虑下图

显然地,这张图的最小生成树是

其实建重构树的过程差不多,一共两步循环操作
- 将所有边按边权从小到大排序
- 每次找最小的一条边,如果条边相连的两个点在同一个集合中,那么就跳过,否则就将这两个点的祖先都连到一个虚点上去,让这个虚点的点权等于这条边的边权
所以理论上最后建出来的的重构树是这样的:

这棵树有很多独特的性质
- 原本最小生成树上的点在重构树里都是叶节点
- 从任何一个点往根上引一条路径,这条路径经过的点的点权单调不降(最大生成树单调不升)
- 任意两点之间路径的最大边权就是他们的 \(\operatorname{LCA}\) 的点权