P8933 [JRKSJ R7] 技巧性的块速递推 题解

题目传送门

题意：

• 简单来说就是一个涂色游戏。

• 有一个 n×m 的棋盘需要涂色。

• 每格只能涂黑色或白色两种颜色。

• 横、竖、斜连续 3 格颜色不能相同。

• 横、竖、斜连续 4 格颜色不能有 3 个相同颜色，即只能是 2 个黑和 2 个白。

• 最后让你统计出所有符合条件的涂色方式的方案数，并对于 998244353 取模。

思路：

• 因为连续四个格子一定是 2 黑 2 白，所以如果确定了 (i，j) 点任意方向上与其连续的三个点的颜色，就可以推出 (i，j)（即确定的三个中较少的那种颜色）。例如：

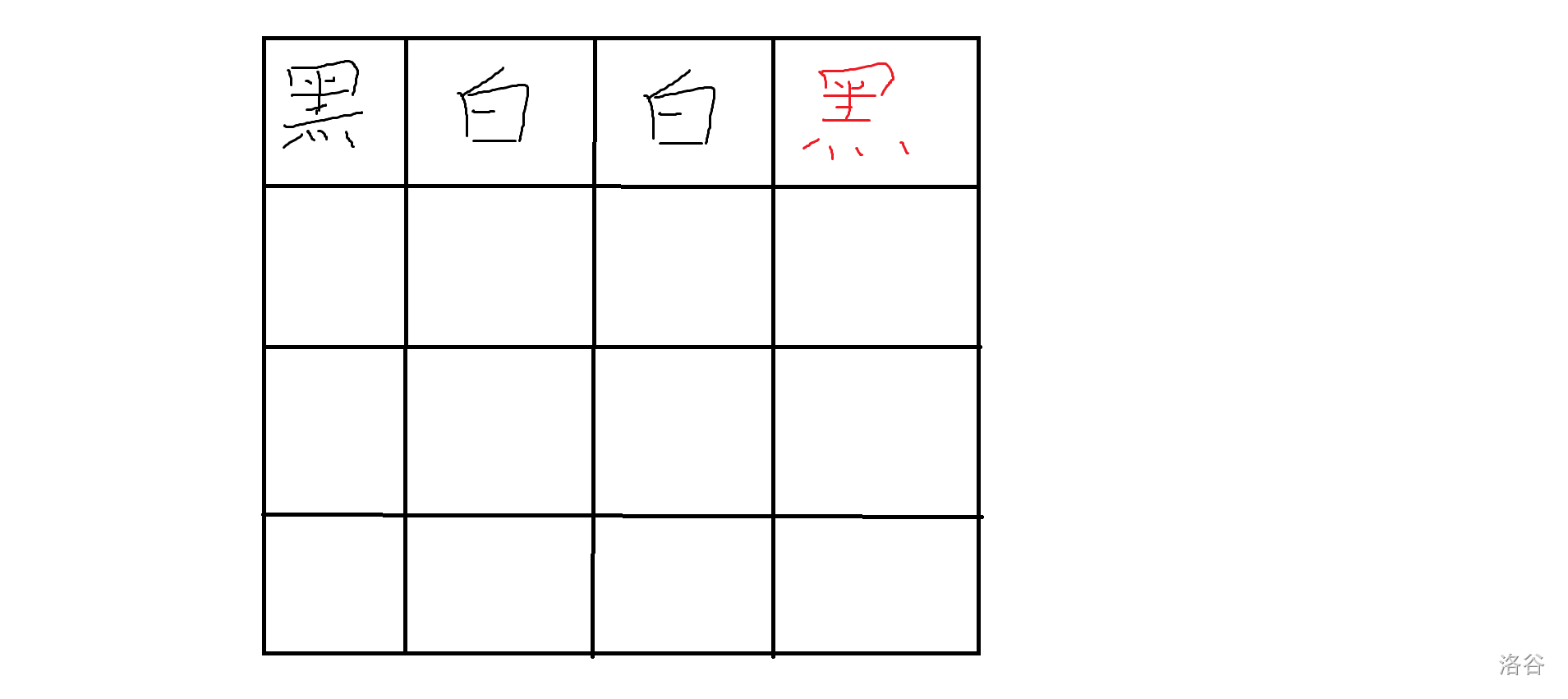
上图中第一行，由于前三个格子已经确定，要想符合条件，第四个只能是较少的黑色。

竖和斜也是同理，图有点丑，就不放了。

• 利用上一个条件我们还可以知道一件事，$(i-4,j)$ 格点与 $(i,j)$ 格点的颜色一定相同。因为根据三个连续格点的颜色就能确定与其相邻的第四个点的颜色，由于这两个点中间三个点是一定的，所以确定的第四个点的颜色也是一定的，所以这两个点的颜色一定一样的。因此这个棋盘其实是由一个 4×4 的小棋盘循环构成的。

• 利用上面的条件就可以扩展出整个棋盘，不过在斜方向上可能会出问题，我们知道，所有斜行出问题的情况最多只会到 7×7 的范围，因此当 n 或者 m 超过 7 时，可以转化为 7。例如：n=5，m=20 的情况就相当于 n=5，m=7 的情况。

• 利用这几个条件就可以开始搜索了：

1. 搜索的简单框架还是很好想的：每次搜一个点，枚举是黑是白，然后接着搜下一个点，当整个棋盘搜索完之后，再去 check 一下，符合的话方案数就加 1。

2. 接下来还要加一个剪枝：因为上面推出的第二个条件，所以当一个点的横坐标 ≥4 时（即存在 (i-3,j)），就可以直接根据 (i-3，j) 点一直到 (i，j) 点间的点求出 $(i，j)$ 点的颜色，没必要再枚举。

3. 不过不能问一次搜一次，因为 T≤10^5，会时超。这时可以先预处理出 7×7 范围所有大小的方阵答案，询问时直接输出，就不会时超了。

代码：

请勿抄袭。

#include<bits/stdc++.h>
using namespace std;
int n,m,ans;//矩阵的长宽，方案数 
int a[10][10];//矩阵，1表示黑，0表示白 
int p[10][10];//预处理数组，记录答案 
inline bool check()//判断当前填法是否合法 
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(i+2<=n)//横向3个颜色不能一样 
			{
				if(a[i][j]==a[i+1][j]&&a[i][j]==a[i+2][j]) return 0;
			}
			if(j+2<=m)//竖向3个颜色不能一样  
			{
				if(a[i][j]==a[i][j+1]&&a[i][j]==a[i][j+2]) return 0;
			}
			if(i+2<=n&&j+2<=m)//右下斜线向3个颜色不能一样 
			{
				if(a[i][j]==a[i+1][j+1]&&a[i][j]==a[i+2][j+2]) return 0;
			}
			if(i-2>=1&&j+2<=m)//右上斜线向3个颜色不能一样  
			{
				if(a[i][j]==a[i-1][j+1]&&a[i][j]==a[i-2][j+2]) return 0;
			}
			/*上面四个条件之所以不判断前面的方向，是因为在前面的循环已经判断过了，向后判断即可*/
			if(i+3<=n)//横向4个不能有3个一样 
			{
				int sum1=0,sum2=0;//黑与白的个数 
				for(int k=i;k<=i+3;k++)
				{
					if(a[k][j]) sum1++;
					else sum2++;
				} 
				if(sum1>=3||sum2>=3) return 0; 
			}
			if(j+3<=m)//同上 
			{
				int sum1=0,sum2=0;
				for(int k=j;k<=j+3;k++)
				{
					if(a[i][k]) sum1++;
					else sum2++;
				} 
				if(sum1>=3||sum2>=3) return 0; 
			}
			if(i+3<=n&&j+3<=m)
			{
				int sum1=0,sum2=0;
				for(int k=0;k<=3;k++)
				{
					if(a[i+k][j+k]) sum1++;
					else sum2++;
				} 
				if(sum1>=3||sum2>=3) return 0;
			}
			if(i-3>=1&&j+3<=m)
			{
				int sum1=0,sum2=0;
				for(int k=0;k<=3;k++)
				{
					if(a[i-k][j+k]) sum1++;
					else sum2++;
				} 
				if(sum1>=3||sum2>=3) return 0;
			}
		}
	}
	return 1;//前面都没return说明合法 
}
inline void dfs(int x,int y)//搜索，x和y表示当前搜索的点 
{
	if(y>m) y=1,x++;//搜完一行则换行 
	if(x>n)//说明全搜完了 
	{
		if(check()) ans++;//合法则方案数加1 
		return;
	}
	if(y>=4)//剪枝，≥4则可以直接确定 
	{
		int sum1=0,sum2=0;
		for(int i=y-3;i<=y-1;i++)//统计颜色 
		{
			if(a[x][i]) sum1++;
			else sum2++;
		}
		if(!sum1||!sum2) return;//如果不合法，则没有搜的必要，直接return 
		if(sum1==1) a[x][y]=1;
		if(sum2==1) a[x][y]=0;
		//取少的作为当前点的颜色 
		dfs(x,y+1);//继续搜索 
		return;
	}
	a[x][y]=1;dfs(x,y+1);
	//涂黑 
	a[x][y]=0;dfs(x,y+1);
	//涂白 
}
int main()
{
	for(int i=1;i<=7;i++)
	{
		for(int j=1;j<=7;j++)
		{
			n=i,m=j;
			ans=0;
			dfs(1,1);
			p[i][j]=ans%998244353;
		}
	}//预处理 
	int T;
	cin>>T;
	while(T--)//询问 
	{
		scanf("%d%d",&n,&m);
		if(n>7) n=7;
		if(m>7) m=7;
		//>7 时可以转化为7的情况 
		printf("%d\n",p[n][m]);
	}
	return 0;
} 

写题解不易，点个赞呗。